Тасымалдау есебі ұғымы
Жоспар
Кіріспе
- Жалпы бөлімЭкономикалық есептердің математикалық модельдерін құруТасымалдау есебі ұғымы
- Арнайы бөлімТасымалдау есебін шешуMS Excel ортасында тасымалдау есебін шешу
Қорытынды
Қолданылған әдебиеттер
Кіріспе
“Модель” термині әр түрлі адамдардың қызметтері ортасында қолданылады және көптеген мағыналық түсініктері бар. Біз тек білім алудың құралы болып табылатын “модельдерді” қарастырамыз.
Модель - бұл зерттеулердің бір әдісі болып табылады.
Экономика-математикалық моделін құру есебі экономикалық оқиға “экономика тілінен” “математика тіліне” аударуды ұсынады және белгілі бір ережелерге бағынады. Ешқандай модель зерттеу құбылыстың толық бейнесі болуы мүмкін емес екені айқын. Осыған байланысты “модель” бейне болып қарастырылады немесе құбылысты зерттеу, әртүрлі жағдайлар көмегімен объектілерді зерттеу орындалады. Модель объектінің тек маңызды кескіннің қарапайым схемаланған абстрактты түрде бейнелеу керек.
Модельді құру объектінің ең маңызды белгісін таңдауынан басталады, нақты ғылыми теориясына тіркелу мүмкіндігін береді, зерттелетін процестің заңдылығын ашу. Сонымен қатар осындай модельдеу алдына қойылған практикалық, нақтылы есептерге бағыну керек. Осыған байланысты модельдеу кезінде экономика объектілері күрделі динамикалық жүйе түрінде қарастырылады. Модельдер теориясы теоретикалық-кибернетиканың бөлігі болып табылады. Экономикалық статистикалық мінездемесі экономикалық жүйенің құрылымымен анықталады
Сонымен модельдеу тек талдау тәсілі ғана емес және де практикалық шешімдерді қабылдау қоры деп қарастырылады.
Тасымалдау есебін орындау кезінде, біз жүкті тасымалдау шығынын едәуір азайту негізінде кәсіпорынның ресурстарын үнемдеуге көмектесетін жұмыс жазамын.
Менің курстық жұмысымның тақырыбы «Excel ортасында тасымалдау есебін шешу» болып табылады.
Курстық жұмысты жазу барысында экономикалық есептердің математикалық модельдерін құру, тасымалдау есебі ұғымдарының мәнін ашамын. Тасымалдау есебін жүргізу ережелерін қарастырамын. Қазіргі заманғы компьютерлік технологияларды қолданып осы экономика-математикалық есептерді шешуде қолданылатын бағдарламалар туралы ақпарат жазамын. Нақты айтқанда тасымалдау есебін Excel ортасында шешу мысалдарын қарастырамын.
- Жалпы бөлім
1. 1. Экономикалық есептердің математикалық модельдерін құру
Сызықтық бағдарламалау есебі былай анықталады.
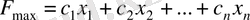(1. 1)
функциясының кризистік мәні келесі шектеулерді қанағаттандыратын
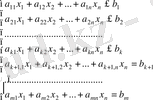(1. 2)
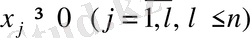, (1. 3)
есеп сызықтық бағдарламалаудың жалпы есебі деп аталады.
(1. 2) жүйесі шектеулер жүйесі деп аталады, ал (1. 1) сызықтық функция - мақсатты функция .
Сызықтық бағдарламалау есебінің қысқаша жазылуы:
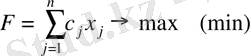(1. 4)
мынадай шектеулерге қанағаттандырады:
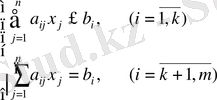(1. 5)
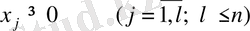(1. 6)
(1. 5), (1. 6) шектеулерін канағаттандыратын
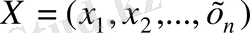вектор
мүмкін оң шешім
(
жоспар
) деп аталады.
Егер
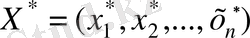жоспар үшін (1. 4) мақсатты функция максималды немесе минималды мән қабылдаса, онда ол
оптималды жоспар
деп аталады.
Егер (1. 5) шектеулер жүйесі тек теңсіздіктерден тұратын болса, онда сызықтық бағдарламалау есебінің мұндай түрі стандартты ( симметриялық ) деп аталады; егер (1. 5) шектеулер жүйесі тек теңдіктерден тұратын болса, онда сызықтық бағдарламалау есебінің мұндай түрі канондық ( негізгі ) деп аталады.
Кез келген сызықтық бағдарламалау есебін канондық, стандарты немесе жалпы түрге келтіруге болады.
Қосымша
,
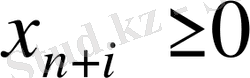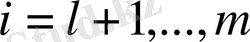айнымалыларын енгізіп, (1. 2) шектеу-теңсіздіктерін теңдеу ретінде жазуға болады:
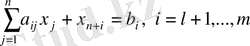
Егер шектеулер жүйесінде теңсіздіктер «≥» таңбасымен берілсе, онда сәйкес қосымша айнымалыларды «-» таңбасымен енгізу керек.
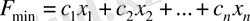функциясының минимумын анықтау есебін функцияның максимумын табу есебімен алмастыру үшін оны «-1»-ге кобейту қажет:
.
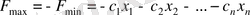Көп жағдайда есептің векторлық түрі қолданылады:
(1. 7)
анықтау керек, егер
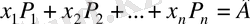, (1. 8)
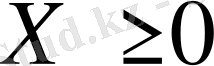, (1. 9)
мұнда
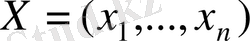- белгісіздер векторы,
-
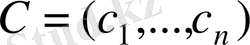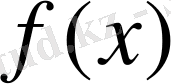мақсатты функциядағы коэффициенттерден құралған вектор;
, -
-өлшемді вектор-бағаналар, бұлар есептің шектеулер жүйесінің белгісіздер коэффициенттерінен және бос мүшелерден құралған:
,
-
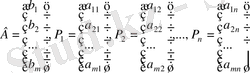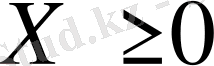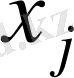белгісіз айнымалылар шамаларының теріс емес екендігін көрсететін қысқаша жазу түрі.
Келесі түрдегі экономикалық есептер: шикізатты қолдану есебі, азық құрамын құру есебі, тасымалдау есебі үшін есептің жалпы қойылымы және оған модель құруын қарастырайық.
1. Шикізатты пайдалану есебі
(
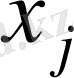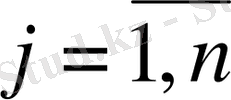) - өндіруге арналған
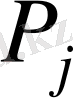өнімінің даналар саны;
(
) -
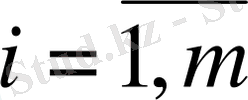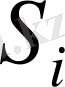шикізатының қоры;
(
) -
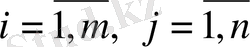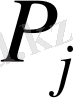өнімінің бірлігін шығаруға кететін
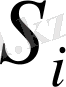шикізатының бірліктер саны;
(
) -
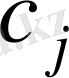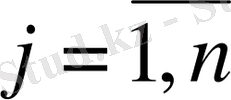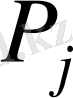өнімінің бірлігін сатудан түсетін пайда болсын.
Онда шикізатты пайдалану есебінің экономика-математикалық моделі келесі түде жазылады:
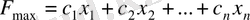(1. 10)
мақсатты функция келесі шектеулерге қанағаттандырып:
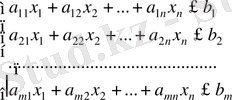(1. 11)
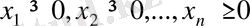(1. 12)
максималды мән қабылдау үшін өнімді шығаратын
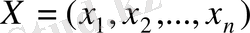жоспарын табу керек.
2. Азық құрамын құру есебі
(
) -
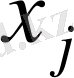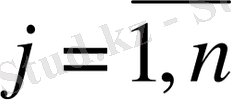түрі жемінің бірліктер саны;
(
) -
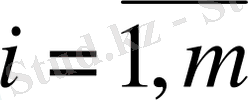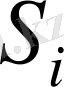нәрлі затының азық құрамында болуының қажетті минимумы;
(
) -
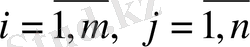түрі жемінің бірлігіндегі
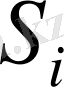нәрлі затының бірліктер саны;
(
) -
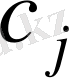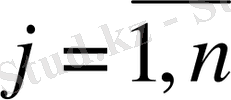түрі жем бірлігінің құны болсын.
Онда азық құрамын құру туралы есебінің экономика-математикалық моделі келесі түде жазылады:
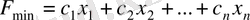(1. 13)
мақсатты функция келесі шектеулерге қанағаттандырып:
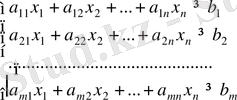(1. 14)
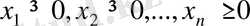(1. 15)
минималды мән қабылдау үшін тиімді болатын
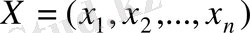жоспарын табу керек.
3. Тасымалдау есебі
(
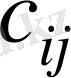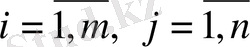) - жүк жіберетін
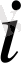пунктінен қабылдайтын
пунктіне дейін жүктің бір бірлігін тасымалдау тарифі;
(
) -
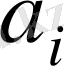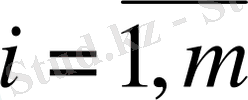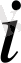-ші қойма пунктіндегі тауар қоры;
(
) -
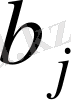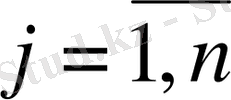-ші қабылдау пунктіндегі жүк қажеттілігі;
(
) -
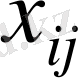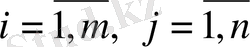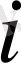-ші жіберу пунктінен
-шы қабылдау пунктіне тасымалданатын жүк бірліктерінің саны болсын.
Онда тасымалдау есебінің экономика-математикалық моделі келесі функцияның минимумын анықтаудан құралады:
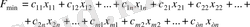(1. 16)
және ол келесі шарттарды қанағаттандыруға тиіс:
(1. 17)
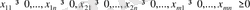(1. 18)
1. 2. Тасымалдау есебі ұғымы
Тасымалдау есебінің
жалпы қойылымы
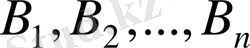
қабылдау пунктеріне жіберіленетін
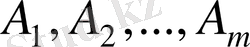пунктерінен қандайда біртектес жүк тасымалдауының оптимал жоспарын анықтаудан құралады. Оптималдық критерий ретінде немесе барлық жүктің тасымалдау бағасының минималдысы немесе оның жеткізу уақытының минималдысы алынады.
Белгілеу енгізейік.
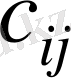- жүкті жіберетін
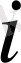-ші пунктінен
-ші қабылдау пунктіне дейін жүктің бірлігін тасымалдау тарифі;
- жүк жіберетін
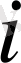-ші пунктегі жүк қоры
;
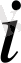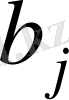- жүк қабылдайтын
-ші пунктегі жүкте қажеттілігі;
-
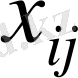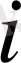-ші жүк жіберетін пунктен
-ші жүкті қабылдау пунктіне дейін тасымалданатын жүктер бірлігі.
Онда есептің экономикалық-математикалық қойылымы келесі мақсатты функцияның минималды мәнін анықтаудан тұрады:
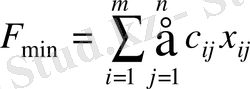(1)
және ол келесі шарттарды қанағаттандырады
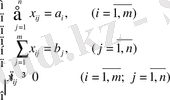(2)
Егер тағайындау пунктерінде жүк қажеттілігі тасымалдау пунктеріндегі жүк қорына тең болса, яғни
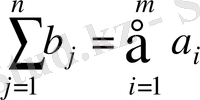(3)
онда тасымалдау есебінің моделі жабық деп аталады. Егер бұл шарт орындалмаса, онда - ашық .
Әдітте тасымалдау есебінің берілу шарттары таблица түрінде жазылады.
c 11
x 11
c 12
x 12
c 1j
x 1j
c 1n
x 1n
c 21
x 21
c 22
x 22
c 2j
x 2j
c 2n
x 2n
c i1
x i1
c i2
x i2
c ij
x ij
c in
x in
c m1
x m1
c m2
x m2
c mj
x mj
c mn
x mn
Жүк қоры қажеттіліктен артық немесе қажеттілік қордан артық болса, онда тарифі нөлге тең болатын жалған қажеттілік пункті немесе жалған жүк жіберу пункті тағайындалады.
Тасымалдау есебіндегі
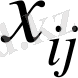айнымалыларының саны
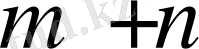тең, ал (2) жүйесіндегі теңдеулер саны
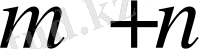тең. (3) шарты орындалғандықтан, сызықтық тәуелсіз теңдеулер саны
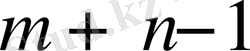тең. Соның салдарынан, тасымалдау есебінің тіреуіш жоспары нөлге тең емес
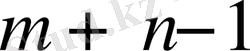белгісіздерден тура алады (яғни толтырылған есептер саны
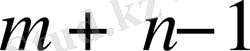тең) .
Егер тіреуіш жоспардағы нөлге тең емес компоненттер саны
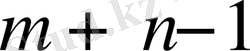тең болса (яғни толтырылған ұяшықтар саны
болса), онда жоспар
ерекшеленбеген
болады
,
ал егер
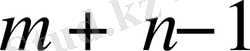-нен кем болса, онда -
ерекшеленген
(онда орнына қоятын нөлдік мәнді енгізу керек) .
Тіреуіш жоспарды анықтау үшін бірнеше әдіс бар. Олардың арасында «солтүстік батыс» әдісі және «минималды элемент» әдісі.
Оптимал жоспарды анықтау үшін «потенциалдар» әдісі және «дифференциалды ренталар» әдісі бар.
«Солтүстік батыс» әдісі:
шарттар таблицасының ұяшықтарын толтыру
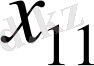белгісізі үшін сол жақтағы жоғарғы бұрыштан босталады және
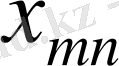белгісізімен аяқталады.
«Минималды элемент» әдісі:
шарттар таблицасының ұяшықтарын толтыру минимал
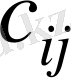тарифі ұяшығынан басталады.
Екінші әдіс едәуір тиімді болып келеді.
Потенциалдар әдісі
Егер тасымалдау есебінің қандай да бір
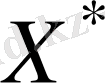жоспары үшін
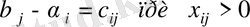(толтырылған ұяшықтар үшін) (4) және
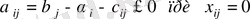(бос ұяшықтар үшін) (5)
болатындай
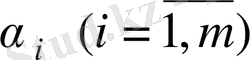және
сандары бар болса, онда құрастырылған
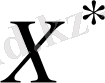жоспары тасымалдау есебінің
оптимал жоспары
болады.
және
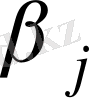сандары сәйкес жіберілу және қабылдау пунктерінің
потенциалдары
деп аталады.
Берілген
және
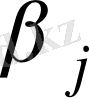сандарын (4) теңдеулер жүйесінен табады, мұнда
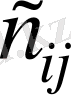- шығандар тарифі. Толтырылған ұяшықтар саны
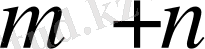болғандықтан, (8. 6) жүйісіндегі
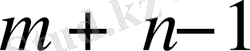теңдеуден тұрады. Белгісіздер саны теңдеулер санына біргі көп болғандықтан, белгісіздердің біреуін кез келген сан ретінде алу болады,
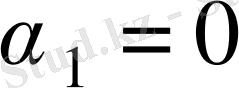болсын, және (4) -тең рет бойынша қалған айнымалылардың мәндерін табуға болады. Осыдан кейін (5) формуласы бофынша әрбір бос ұяшық үшін
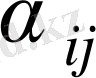сандарын табамыз. Егер барлық
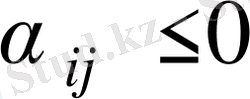болса, онда
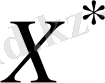жоспары оптимал болады. Егер жоқ дегенде бір
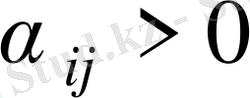болса, онда жоспар оптимал болмайды және жаңа жаңа тіреуіш жоспарға көшу қажет.
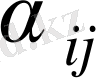арасында максимал оң сан таңдайды және осы ұяшықты толтырады. Осымен қатар жаңадан есептеу циклін құрады.
Тасымалдау есебінің шарттар таблицасында төбелері таблицаның толтырылған ұяшықтарында орналасқан, ал қабырғалары - бағана және жол бойында орналасқан сынықты цикл деп атайды.
Егер сынықтың сызықтары қиылысса, онда өзін-өзі қию нүктелері төбелер болмайды. Циклдарға мысалдар:
Осыдан кейін жеткізулерді алмастырады:
1) берілген бос ұяшықпен цикл арқылы байланысқан әрбір ұяшыққа қандай да бір таңба тағайындайды. Сонда, бос ұяшыққа «+» таңбасын, ал басқаларына - кезектесіп «-» және «+».
2) осы бос ұяшыққа таңбасы «-» болатын
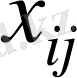сандарының ең кішісі көшіріледі. Осымен қатар бұл санды таңбасы «+» болатын (шешуші) ұяшықтарға қосадыда, таңбасы «-» болатын ұяшықтағы сандардан алады.
Бос ұяшыққа сан жазылады, ал минималды тасымалдауы бар ұяшық - бос ұяшық болады. Осының нәтижесінде жаңа тіреуіш жоспарды табамыз және оны оптималдыққа тексереміз.
Тасымалдау есебінің алгоритмі
- Тіреуіш жоспарды табады. Толтырылған ұяшықтар саны-ге тең болуы керек.
- жәнепотенциалдарын табады.
- Бос ұяшықтар үшінтабады. Егер барлықболса, онда жоспар оптималды, ал егерболса, онда жаңа тіреуіш жоспарға көшеді.
- арасында максималдыны таңдайды және қайта санау циклін құрады
- Табылған жоспарды оптималдыққа тексереді, яғни 2 қадамға көшеді.
2. Арнайы бөлім
2. 1. Тасымалдау есебін шешу
Есеп 1. Тасымалдау есебінің жүк тасу жоспарының оптималдысын тап:
Үш
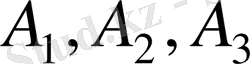қоймаларына сәйкес біртектес жүк 50, 30 және 10 бірлікке тең мөлшерде түседі. Осы жүкті төрт
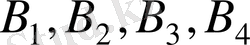қабылдау пунктеріне сәйкес 30, 20, 10 және 20 бірлік мөлшерінде тасымалдау керек. Жүктің бірлігін көшіру тарифі таблицада берілді.
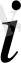-ші жіберу пунктінен
-ші пунктке жіберілетін жүк санының бірліктері
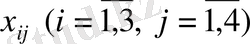болсын. Онда есептің экономикалы-математикалық моделі мынадай болады:
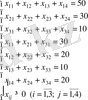
шарттарды қанағаттандыратын:
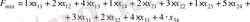
анықтау керек.
Шешуі.
(3) шарты орындалмағандықтан берілген есептің моделі ашық болады. Қор қажеттіліктен 10 бірлікке артық, сондықтан нөлдік тарифпен «ЖП» жасанды қабылдау пунктін қосамыз және оның жүк қажеттілігі 10 бірлікке тең. Есептің жабық моделіне келеміз. «Солтүстік шығыс» бұрыш әдісі бойынша
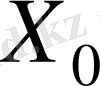тіреуіш жоспарын құрамыз. Ұяшықтарды толтыруды
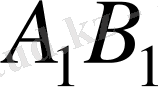ұяшығынан бастаймыз, мұнда
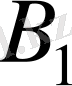қажеттілігін және
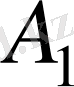қор мөлшерін ескереміз, одан кейін
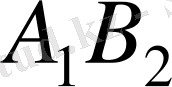-ні толтырамыз және т. с. с. қордың барлығы қолданылып, ал қажеттіліктің барлығы өтелгенше. Келесі таблицаны аламыз:
1
30
2
20
1
10
5
20
0
10
Тіреуіш жоспарды матрица түрінде жазамыз
,
бұл жағдайда тасымалдудың жалпы құны мынаны құрайды:
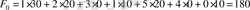(шартты ақша бірлігі) .
Алынған тіреуіш жоспарды оптималдыққа тексереміз.
Толтырылған ұяшықтар саны 5-ке тең, ал ол
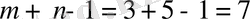тең болуы тиіс. Сондықтан бұл есептің шешімі болмайды. Бір жолдың толтырылған ұяшықтарынан басқа жолдың толтырылған ұяшықтарына көшу «сатылары» үзілетін ұяшықтарға нөлдік тасымалдарды қосайық, яғни, мысалы,
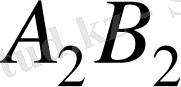және
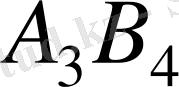ұяшықтарына.
(4) формуланы қолданып
және
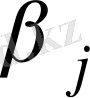есептейік. Келесі теңдеулер жүйесі шығады:
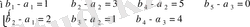
Бұл жүйе 7 теңдеуден және 8 белгісізден тұрады. Сондықтан
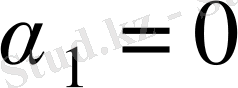дейміз. Онда
,
,
,
,
,
,
.
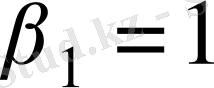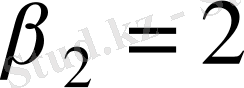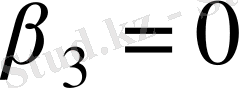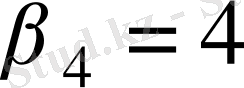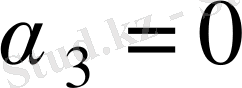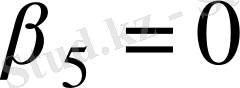және
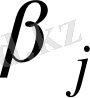потенциалдар мәндері жазылатын қосымша жолмен бағананы таблицаға қосайық.
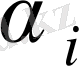
1
30
- 2
20
+ 1
3
+ 3
0
1
10
- 5
20
0
1
4
0
0
10
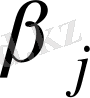
Енді (8. 6) формуласы бойынша бос ұяшықтар үшін
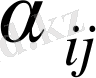есптейік.
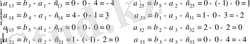
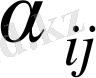арасында оң сандар бар болғандықтан (3 және 1)
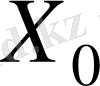жоспары оптимал болмайды. Осы оң бағаларды
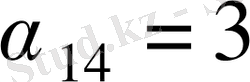
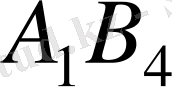ұяшығына және
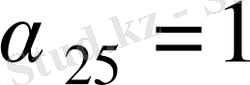
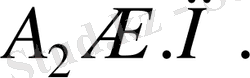ұяшығына жазайық. Осылардың арасынан ең үлкен бағаны таңдап оны дөнгелектейік.
Осы баға орналасқан ұяшықтан бастап, цикл төбелері толтырылған ұяшықтарда болатындай, жаңадан санау циклын құрамыз.
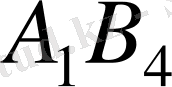ұяшығына «+» таңбасын тағайындаймыз, ал цикл төбелерінде орналасқан басқа ұяшықтарға кезектесіп «-» және «+» таңбаларын тағайындаймыз. Минус таңбасы орналасқан ұяшықтардағы ең кіші мән 20. Осы санды «+» таңбалары орналасқан ұяшықтардағы сандарға қосамыз, ал «-» таңбасы орналасқан ұяшықтағы сандардан аламыз.
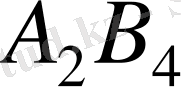ұяшығы бос, ал
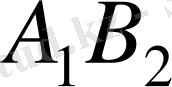нөлдік жеткізумен толтырып қалған болсын.
Жаңа таблицаға және жаңа тіреуіш
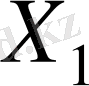жоспарына көшеміз.
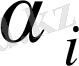
1
30
- 2
0
+ 1
20
3
20
1
10
3
1
+ 2
3
- 4
0
0
10
,
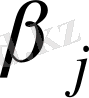
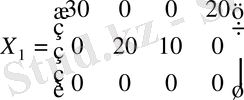мұнда
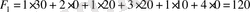(келісілген ақша бірлігі) . Функция мәні азайды.
Бұл жоспарды оптималдыққа тексереміз.
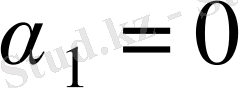болсын. (4) формуласы бойынша табылған
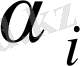және
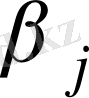мәндерді таблицаға жазамыз, ал оң
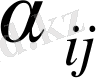мәндерін бос ұяшықтар үшін есептейік және оларды дөнгелектейік. Екі оң
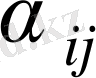бар:
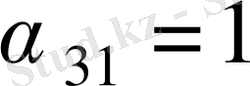және
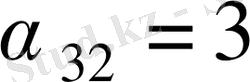. Бұлардың ең үлкенін таңдап, яғни 3 санын, жаңадан санау циклін құрамыз. Минусы бар ұяшықтарда нөлдер тұр. Сондықтан келесі таблицада 0 саның қосып және алғаннан
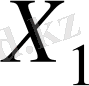жоспарыны өзгермейді.
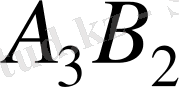ұяшығы нөлдік жеткізілумен толтырылады, ал минусы бар ұяшықтардын біреуі бос болып, екіншісі нөлдік жеткізілумен толтырылуы қажет.
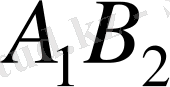бос, ал
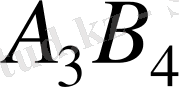- нөлдік болсын. Жаңа таблицамен жаңа жоспарға келеміз
,
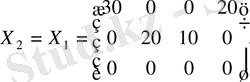мұнда
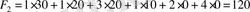(келісілген ақша бірлігі) .
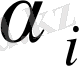
- 1
30
+ 1
20
+ 2
3
- 3
20
1
10
0
1
3
1
+ 2
0
- 4
0
0
10
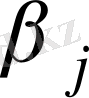
Бұл жоспарды оптималдыққа тексереміз.
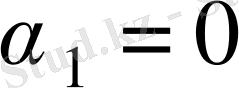болсын.
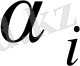және
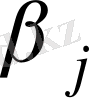мәндерін, ал бос ұяшықтар үшін
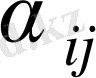мәндерін есептейік. Үш оң
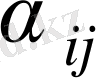бар:
,
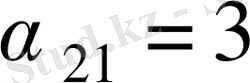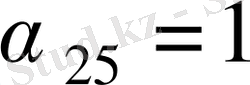и
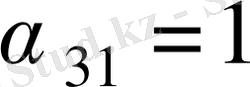. Бұлардың ең үлкенін таңдап, яғни 3 санын, жаңадан санау циклін құрамыз. Минусы бар ұяшықтардағы ең кіші жеткізу нөл. Сондықтан келесі таблицада 0 саның қосып және алғаннан
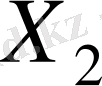жоспарыны өзгермейді.
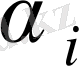
1
30
1
20
2
0
- 3
20
1
10
+ 0
1
+ 2
0
- 0
10
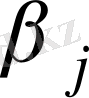
Мұнда
, сондықтан
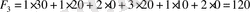(келісілген ақша бірлігі) .
Жоспарды оптималдыққа тексереміз.
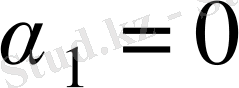болсын.
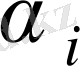және
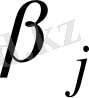мәндерін, ал бос ұяшықтар үшін
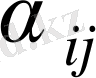мәндерін есептейік.
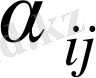мәндерінің арасында бір оң мән бар:
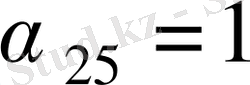. Цикл құрамыз. Минусы бар ұяшықтардағы ең кіші мән 10. Осы санды плюс орналасқан ұяшықтардағы мәндерге қосымыз және минусы бар ұяшықтардан алып тастаймыз. Жаңа таблицаға келеміз:
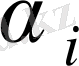
1
30
1
20
2
0
3
10
1
10
0
10
2
10
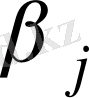
Жаңа жоспар:
және
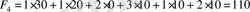(келісілген ақша бірлігі) .
Оптималдыққа тексереміз.
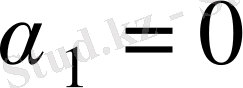болсын.
және
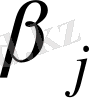, бос ұяшықтар үшін
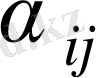есептейміз. Барлық
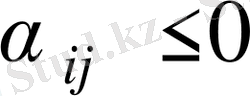. Сондықтан алынған
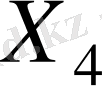жоспары оптимал болады, яғни
, болғанда
(келісілген ақша бірлігі) .
Есеп 2. Алдында келтірілген есеп 1-ге «минимал элемент» әдісімен тіреуіш жоспарды құр.
Ұяшықтарды толтыруды минималды
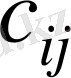тарифі бар ұяшықтан бастаймыз. Ең кіші тариф 1-ге тең және бұндай үш ұяшық бар. Сондықтан толтыруды осындай ұяшықтың кез келгенінен бастаймыз. Мысалы, жүк қажеттілігін және бар қорды ескере отырып алдымен
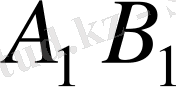ұяшығын, содан кейін
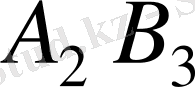және
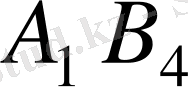ұяшықтарын толтырамыз.
1
30
1
20
3
10
1
10
0
10
2
10
,
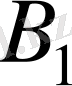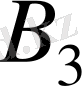және
пунктерінің жүк қажеттілігі толығымен қанағаттандырылды, ал
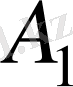пунктінің жүк қоры толығымен қолданылды, сондықтан толтырымлмай қалған
,
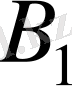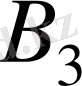және
бағаналарының және
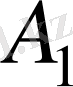жолының ұяшықтары жүк тасымалдауынан шығарылып тасталады.
Содан кейін тарифі 2-ге тең ұяшық, одан кейін тарифі 3-ке тең, және т. с. с. барлық қор пайдаланылғанша, ал қажеттілік қанағаттандырылғанша толтырылады.
тіреуіш жоспарына келеміз,
бұл мәндер үшін мақсатты функция мынадай болады:
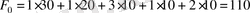(келісілген ақша бірлігі) .
Табылған жоспар оптималға тең болады, яғни
және
.
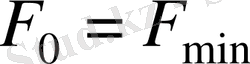2. 2. MS Excel ортасында тасымалдау есебін шешу
Мысал 1. Тасымалдау есебіне мысал ретінде 2 қойма және 5 дүкен үшін қарастырамыз.
C4:C5 ұяшықтарына 2 қоймадағы бар тауарлардың көлемін жазамыз.
E5:I5 ұяшықтарына дүкендерден түскен тауарларға деген сұранымдарды жазамыз
B8:F9 ұяшықтарына транспорттық матрица шығынын, яғни I-ші қоймадан J-шы дүкенге баратын тауар санының шығынын енгіземіз
B13:F14 ұяшықтарына тасымалдау жоспары - I-ші қоймадан J-шы дүкенге тасымалданған тауар санының матрицасы енгізіледі.
D15 ұяшығына - мақсат функцияны енгіземіз:
{ =СУММПРОИЗВ((B8:F9*B13:F14) ) }
D17:H17 ұяшықтарына шектеулер енгіземіз, әр дүкенге қажетті сұранымды қанағаттандыру үшін. Келесідей формула жазамыз:
{=СУММ(B13:B14) - E5 }
Содан кейін автотолтыру көмегімен қалған ұяшықтарды толтырамыз.
Келесі шектеулер тобын береміз. Бұл шектеулер қоймадағы тауардан асып көп тауар тасымалдауға кетіп қалмау үшін жасалады. D18 формула енгіеміз. Ол мына түрде:
{=C4 - СУММ(B13:F13) }
Бұл формуланы баған бойынша толтырамыз, яғни D19 ұяшығына. Дайындық кезеңі аяқталды енді шешу құралын шақыру керек.
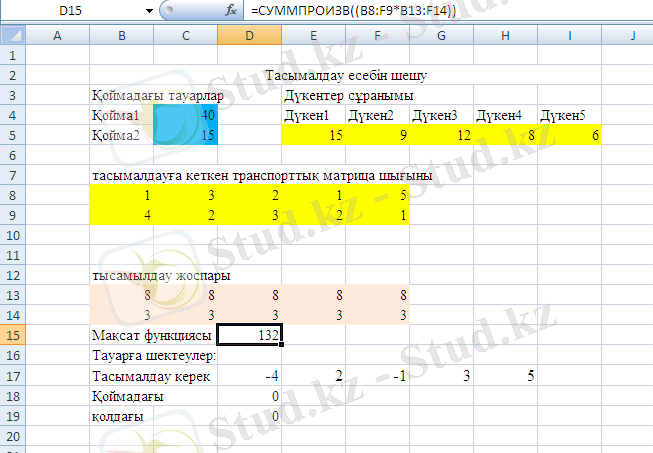
Мақсат функциясы орналасқан ұяшыққа көрсеткішті орнатамыз (ол бізде D15 ұяшығы) да, «Поиск решения» құралын шақырамыз. Төмендегі бейнеге қарап терезені толтырамыз:
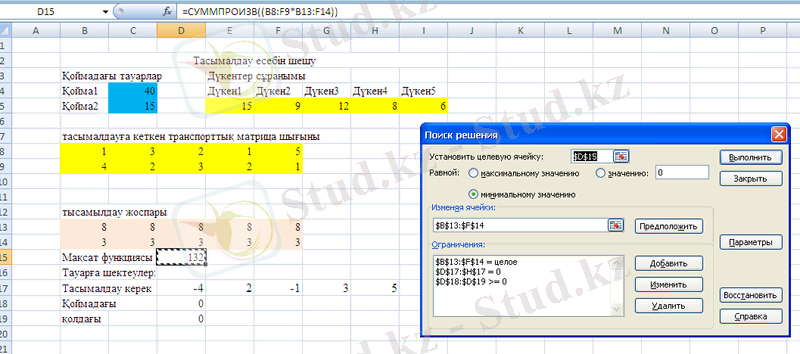
Тасымалдау есебін шешудегі «Поиск решения» терезесі
Тапсырманы орындауға жібермес бұрын «Параметры» терезесін ашып тексереміз. Өзгертулер енгіземіз. Терезе келесі түрде болады:
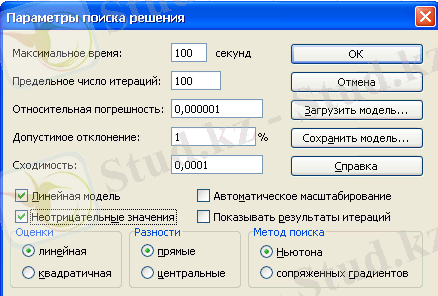
Тасымалдау есебін шешудегі «Поиск решения» терезесінің параметрлерін ұйымдастыру
«Орындау» батырмасын басып тасымалдаудың оптималды жоспарын алу қалды.
Жасалған жұмысқа қарап тасымалдау шығындарының қаншалықты азайғандығын көруге болады.
... жалғасыСіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz