Циклдік группаның кез келген ішкі группасы циклдік группа

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 18 бет
Таңдаулыға:

МАЗМҰНЫ

Кіріспе . . . 3

1. Топтар теориясынң негізгі ұғымдары . . . 4

2. Ақырлы индексті ішкі топтар . . . 16

3. Қорытынды . . . 20

4. Әдебиет . . . 21

К І Р І С П Е

Маңыздылығы. Топтар идеясының қазіргі айқындалған түріне келуі үшін жалпы алғанда жүз жылдық орны бар көптеген мұрағатты математиктердің жұмыстары пайдаланылды. Лагранждан алгебралық теңдеулерді радикал арқылы шешу үшін қолданылатын ауыстырулар

тобы (1771), Руффини (1799) және Абель (1824) жұмыстары арқылы жеткілікті түсінікті түрде пайдаланылатын Эварист Галуаның топтар идеясы (1830), міне, осы жол - алгебралық теңдеулер теориясы төңірегіндегі дамыған идея.

XIX ғасырдың ортасында тұтас көне геометрияның орнына көптеген «геометрия» келгенде, тәуелсіз және басқа себептерге байланысты бұл идея геометрияда да туындап, бұлардың арасындағы байланыс пен туыстықты айқындау туралы сұрақ қырыннан қойылды. Бұл сұрақтын шешу, яғни көптеген геометрияларды кластарға бөлу жолын Клейннің(1872) «Эрлангендік бағдарламасы» көрсетті. Бұл бағдамалардың негізінде түрлендіру топтар ұғымы жатыр.

Қазіргі математиканың негізі болып табылатын топтар теориясы, сол математиканың аса жан-жақты құралы, топологияның әр түрлі объектілерінің қасиеттерін анық кескіндейтін, алгоритмдер теориясының сынақ орны, күрделі алгебралық жүйелердің аса қажетті құрамдас бөлімі.

Сонымен қатар топтар шындық өмірдің терең заңдылықтарының ең маңыздысы болып табылатын - симметрияны танып білудегі қуатты құрал.

Ертеден келе жатқан, бұрынғыша топтар теориясының қарқынды дамуының тармағы ақырлы топтар теориясы болып табылады. Ол Галуа теориясына қажеттіліктен пайда болып, ауыстырулар топтар теориясын дамыдты.

Әр ішікі топ бойынша топ іргелес кластарға жіктеледі. Іргелес кластар саны ақырлы болса, онда бұндай ішкі топты ақырлы индексті ішкі топ деп атайды. Дипломдық жұмыста топтардың ақырлы индексті ішкі топтар қарастырылған.

Дипломдық жұмыста қарастырылған есептер [1] және [2] оқулықтардан алынған. Қосымша қажетті теориялық материалдар [3] , [4], [5] оқулықтардан қарастырдым.

Мақсаты . Топтардың ақырлы индексті ішікі топтарын қарастыру және олардың қасиеттерін анықтау.

Жаңашылдығы . Барлық нәтижелерді өз бетімше дәлелдедім және әр нәтиже толық дәлелдеумен негізделген.

1. ТОПТАР ТЕОРИЯСЫНЫҢ НЕГІЗГІ ҰҒЫМДАРЫ

Математиканың қай саласы болмасын жиын және осы жиында берілген амалдар жиыны болып табылады, сондықтан математиканың әр саласын кейбір жұп түрінде қабылдауға болады.

Анықтама. Бізге G жиыны берілсін. Егер кез келген a , b G үшін a * b G шарты орындалса, онда G жиынында * - екі орынды алгебралық амал анықталған деп айтамыз және 〈 G , *〉 түрінде белгілейміз.

Кейде, бұл жағдайда G - жиыны * амалына қатысты тұйықталған жиын депте атайды.

Мысалы, N - натурал сандар жиыны қосу және көбейту амалдарына қатысты тұйықталған жиын.

Анықтама. Егер G жиынында екі орынды алгебралық амал анықталса, онда G жиынын группоид деп атаймыз.

Мысал.

Натурал сандар жиыны қосу амалына қарағанда группоид болады.
Барлық рационал сандар жиыны көбейту амалына қарағанда группоид болады.

Анықтама. Егер G жиыны группоид болып және оның элементтері үшін топтау заңы орындалса, яғни a *( b * c ) =( a * b ) * c , мұндағы a , b , c G , онда G жиынын жартылай топ деп атаймыз.

Мысал. N натурал сандар жиыны, Z бүтін сандар жиындары көбейту амалына қарағанда жартылай группа болады.

Анықтама. А кейбір бос емес жиын, ал ∑ А жиынында берілген амалдар жиыны болсын, онда 〈 А , ∑ 〉 жұбын алгебра деп атаймыз.

Анықтама. Егер 〈 G , *〉 алгебрасында * амалы

* амалы ассоциатты болса, яғниG-ның кез келген үшa, b, cэлементері үшінa*(b*c) = (a*b) *cтеңдігі орындалса;
* амалына қарағандаGжиынында бейтарап (бірлік) элемент табылса:G-ның кез келгенaэлементі үшінa*е=е*а=aтеңдіктері орындалса;
G-ның кез келгенaэлементі үшінb*a=a*b=етеңдігі орындалатынG-даbэлементі табылса

шарттарын қанағаттандырса, онда 〈 G , *〉 алгебрасын топ деп атаймыз.

Мысалдар.

Барлық бүтін сандар жиыныZқосу амалына группа болады.
Нөлден өзгеше барлық рационал сандар жиыныQ* көбейту амалына қарағанда группа болады.

Анықтама. Егер G жиынында a элементі үшін a * a ⁻¹ = a*a ⁻¹ =e болатын a ⁻¹ элементі табылса, онда оны a элементіне кері элемент деп атаймыз.

Теорема 1. Егер G жиыны көбейту амалына қарағанда группа болса, онда оның бір ғана бірлік элементі және кез келген a элементі үшін бір ғана кері элементі болады.

Дәлелдеуі . G группа болғандықтан онда ax=a теңдеуі шешіледі. Сондықтан ae ' _a =a деп алуға болады, мұнда e ^' _e G , e ^' _a элементін a элементінің оң бірлік элементі деп атайды. Осы элементті G группасының кез келген b элементі үшін де оң бірлік, яғни be ^' _a = b болатын көрелік. G группасында ya=b теңдеуі шешілетіндіктен

Be ' _a = ( ya ) e ' _a = y ( ae ' _a ) = ya = b

теңдіктерін аламыз. Сонымен e ' _a G группасының кез келген элементі үшін оң бірлік элементболады. Осы элементті e деп аламыз, сонда be '= b болады. Осы сияқты ya=a теңдеуін шешіп e " сол бірлік элементті табуға болады, яғни e " b = b болатын.

Енді e " e '= e " және e " e '= e ' болатындығы түсінікті, сондықтан e '= e "= e деп аламыз. Сонымен e элементі G группасы үшін бір ғана бірлік элементі болады. Теореманың бірінші белгісі дщәлелденді.

Енді ax=e теңдеуін шешіп, a ₁ ⁻¹ G элементін табамыз, сол сияқты ya=e теңдеуін шешіп, a ₂ ⁻¹ G элементін анықтаймыз.

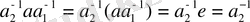
және

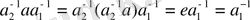
болғандықтан, 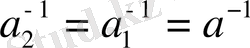деп алуға болады. a элементі үшін a ^-1 біреу болғандықтан түсінікті. Олай болса a ^-1 G элементі a элементі үшін бір ғана кері элемент.

aa ^-1 = a ^-1 a = e

Теорема дәлелденді.

Теорема 2 . Егер G жартылай группасында бір ғана бірлік элемент және кез келген a G ні үшін бір ғана a ^- ¹ =G кері элементі болса , онда G группа болады.

Дәлелдеуі . b , a G болғанда ax=b , ya=b теңдеуінің шешілетінің көрсетілік. a ^-1 ( ax ) = a ^-1 b қатынасынан x = a ⁻¹ b G , ал y = ba ⁻¹ G болатыны түсінікті. Сондықтан, группаның анықтамасы төмендегі түрде айтуға болады.

Анықтама. Егер G жиынында бинарлық алгебралық амал анықталып, осы амалға қарағанда G жартылай группа болса және бір ғана бірлік элементі, онымен бірге әрбір элементене сәйкес бір ғана кері элементі болса, онда G жиынын группа деп атаймыз.

Мысалдар:

Нөльден өзгеше барлық рационал сандарQ* көбейту амалына қарағанда группа.
Нөльден өзгеше барлық нақты сандарR* көбейту амалына қарағанда группа.

G қосу амалына қарағанда группа болса, онда оның бірлік элементін «нөль» деп атаймыз, ал кері элементін «қарама - қарсы» деп атайды.

Анықтама . Егер G группасының H бөлігі группасында анықталған көбейту амалына қарағанда тұйықталған болса, басқаша айтқанда, H жиынының кез келген h ₁ және h ₂ элементтерінің көбейтіндісі H жиынында жатса, онда G группасындағы амал H жиынында анықталған деп атамыз.

Егер осы амалға қарағанда H группа болса, онда оны ( H группасын) G группасының ішкі группасы деп атаймыз. H группасы G групасына ішкі группа болса, онда H G түрінде белгілейміз.

Теорема 3. G группасының H бөлігі ішкі группа болуына қажетті және жеткілікті шарт:

Gгруппасындағы амалдыңHжиынында анықталуы;
Hжиынының кез келген екіh1, h2элементтерінің көбейтіндісіh1*h2Hжиынында жатуы. ;
Hжиынының кез келгенhэлементінің кері элементіh-1-діңH-та жатуы тиіс.

Дәлелдеуі. G группасының H бөлігі G -ға ішкі группа болса, онда аталған шарттардың орындалатындығы түсінікті. Керісінше, аталған шарттар орындалса:

Hжиынында алгебралық амал анықталса;
Топтау заңы бар, өйткені бұл заңGгруппасында орындалады;
Hжиынындыhэлементінің кері элементіh-1бар, яғниh-1H;
Hжиынында бірлік элементe=h*h-1бар.

Сондықтан H жиыны группа. Теорема дәлелденді.

G группасының A және B ішкі жиындарының элементтерінің көбейтіндісін төмендегі түрде белгілейміз.

AB ={ ab │ a A , b B }, A ^-1 ={ a ^-1 │ a A }

Сонда жоғарыдағы теореманы төмендегі түрде жазуға болар еді.

G группасының H бөлігі ішкі группа болуына қажетті және жеткілікті шарт төмендегі қатынастардың орындалуы:

1) H * H H , 2) H ^-1 H

G группасының әрбір a элементенің жәрдемімен ішкі группа жасауға болады. Шындығында, { a }={ a ⁿ │ n Z} жиынын жасауға болады, Z - барлық бүтін сандар жиыны. n натурал сан болғанда a ⁿ = a…a , ал - n теріс бүтін саны үшін

a ^-n = a ^-1 a ^-1 … a ^-1 ; a ⁰ =1

Сонда { a } жиыны G группасына ішкі группа болатыны түсінікті.

Анықтама. G группасының a элементінің жәрдемімен жасалған { a } ішкі группасын циклдік группа деп атаймыз. Сонымен, цикілдік группа әрдайым бір элементтің бүтін санды дәрежелерінен тұрады.

Анықтама. Егер a элементінің барлық бүтін санды дәрежелері әртүрлі болса, онда a элементін шексіз ретті деп санаймыз. Кейде оны O ( a ) = түрінде белгілейміз.

Анықтама. Егер a элементінің барлық бүтін санды дәрежелері әртүрлі болмаса, онда a элементін шекті ( ақырлы ) ретті деп атаймыз.

a элементі шекті ретті болса, онда a ^k = a ¹ , k ≠ l, k >l деп алуға болады, сонда a ^k−1 =1 болар еді. Олай болса a элементінің белгілі бір натурал дәрежесі бірге тең болады. Бұл жағдайда a ⁿ =1, ал a ⁰ , a ¹ , a ² … a ^n-1 элементтері әртүрлі болатын n натурал санын a элементінің реті деп атаймыз. Соныиен, O ( a ) = , не O ( a ) = n болады.

Теорема 4. Егер a элементінің реті n болса, онда a элементінің кез келген бүтін дәрежесі a ⁰ , a ¹ , a ² …a ^n- ¹ элементерінің біріне тең болады.

Дәлелдеуі. a ^n-1 =1 және a ⁰ , a ¹ , a ² … a ^n-1 элементері әртүрлі. Сонда k=n * g + r , 0 ≤ r ≤ n жазуға болады. Олай болса a ^k = ( a ⁿ ) ^q * a ^r = a ^r , 0 ≤ r ≤ n . Дәлелденді.

Теорема 5. Циклдік группаның кез келген ішкі группасы циклдік группа.

Дәлелдеуі. G { a }циклдік группа, H оның өзінен және бірден өзгеше ішкі группасы болсын. Сонда H ішкі группасында жататын a элементтінің ең кіші натурал k дәрежесін табуға болады. Олай болса { a ^k } H болар еді.

Айталық l ≠ 0 (mod k) және a ^l H делік.

Егер l, k бүтін оң сандарының ең үлкен ортақ бөлгіші d болса, онда ku+lv=d теңдігі орындалатын u және v бүтін сандарын табуға болады. Сонда

A ^d =( a ^k ) ^u ( a ^l ) ^v =a ^d H және d<k

Бұл k натурал санын таңдауға қайшылық. Сонымен теорема дәлелденді.

Егер G { a } шекті циклдік группа болса, онда k натурал санына сәйкес G группасының ішкі группасы H { a ^k } табылады. Сонымен, шексіз циклдік группалардың шексіз санды әртүрлі ішкі группалары болады.

Егер G { a } шекті циклдік группа болса, онда H { a ^k }, l ≤ r ≤ n ішкі группа табуға болады.

Теорема 6. егер a элементінің реті n натурал саны болса, онда G ={ a }= G { a ^k }, 0≤ k ≤ n болуына кажетті және жеткілікті шарт k және n сандарының өзара жай сандар болуы.

Дәлелдеуі. ( k, n ) =1 болып, онда ku+nv =1 болатын u және v бүтін сандарын табуға болады.

Сонда ( a ^kn ) =( a ^k ) ^u = a ^1-nv = a * a ^-nv = a

Сонымен ( a ) =( a ^k ) .

Егер ( a ) =( a ^k ) болса, онда a = ( a ^k ) ^s болуы керек.

Олай болса a ^{k s-1} =1, сондықтан ks ≡1 ( mod n ) . Бұдан ks≡1 ( mod n ), олай болса (k, n) =1. Теорема дәлелденді.

Бұл теоремадан байқайтынымыз, егер a элементінің реті n болса, онда n санының кез келген бөлгішіне сәйкес ( a ) циклдік группасының ішкі группасы болады.

Мысалдар.

Z- барлық бүтін сандар жиыны қосу амалына қарағанда группа. СондықтанnZжиыны кез келгенnнатурал саны үшінZгруппасына ішкі группа болады.
Kкомплекс сандар жиынынан нөль санын шығарып тастасақK*=(K-0) жиыны пайда болады. СондаK* жиыны көбейту амалына қарағанда группа болады.

Осы сияқты нөльсіз барлық нақты сандардың жиынын R * түрінде белгілесек, R * жиыны K * группасына ішкі группа болады.

Енді бұл параграфтың соңында группаның жасаушы немесе құрушы элементтері туралы айта кетелік. G группасының бір M шекті жиыны берілсін. M жиыны құрамында жататын G группасынан барлық ішкі группалардың қиылысуын ( M ) түрінде белгілейік. Сонда M жиынын ( M ) ішкі группасының жасаушысы, ал M жиынының элементтерін жасаушы элементтер деп айтамыз. ( M ) группасын кейде гр ( M ) түрінде де белгілейді.

Теорема 7. Егер M-G группасының ішкі жиыны болса , онда

( M ) = { }

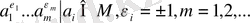Дәлелдеуі. H = { 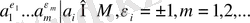} болсын.

H * H H , H ⁻¹ H болатын түсінікті, сондықтан H G группасынан ішкі группа. M жиынының кез келген элементі a _i H - ішкі группасында жатқандықтан ( M ) = H . Дәлелденді.

Мысалдар.

Z=(1) болатын түсінікті, мұндаZ-барлық бүтін сандар жиынының қосу амалына қарағанда группасы.
Q=(1/n│n=1, 2, …), мұндаQ- барлық рационал сандар жиынының қосу амалына қарағанда группасы.
Z*=(-1), мұндаZ*-Zжиынының кері элементі бар элементтерінің жиыны.
Q* =(-1, 2, 3, 5, 7, 11, …, p, …), p- жай сан. Q*-Qжиынының кері элементі бар элементтерінің жиыны немесе нөльден өзгеше барлық рационал сандар жиыны.

Анықтама. G группа. H - G группасының ішкі группасы. Сонда gH= { gh│h H, g G } жиыны G группасының сол іргелес класы деп атаймыз .

Олай болса Hg= { gh│h H, g G } жиыны оң іргелес класы болады.

Егер aH = bH болса, онда a ^-1 b H , ал Ha = Hb , онда ab ^-1 H

Анықтама. a 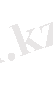~ b a ^-1 b H немесе a 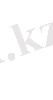~ b ab ^-1 H түрінде бір класта жататын элементтер жиынын белгілейміз. Бұл қатынас G группасында анықталған эквиваленттік қатынас болады.

Шындығында төмендегі шарттарды тексеру болар еді.

a~bb~a
a~a
a~bжәнеb~cондаa~c

Сондықтан G группасы H ішкі группасы бойынша өзара қиылыспайтын іргелес кластардың жиыны түрінде жіктеледі. Бір жағдайда сол іргелес кластарға, ал екінші жағдайда оң іргелес кластарға. Группаның H ішкі группасы бойынша оң іргелес кластардың жиыны мен сол іргелес кластардың жиыны тең қуатты болады, өйткені оны gH Hg ^-1 сәйкестігі анықталады.

Сонымен, G группасының H ішкі группасы бойынша сол іргелес кластарының жиынының қуатын G группасының H ішкі группасы бойынша индексі деп атаймыз және оны 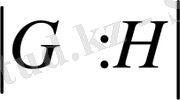түрінде белгілейді. gH класындағы элементтердің саны H ішкі группасындағы элементтердің санына тең, өйткені оны h hg , h H . Сәйкестігі анықталады.

Егер G группасының элементтерінің саны шекті болса, онда 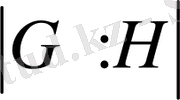саны әрдайым белгілі бір натурал сан болады. Сонымен төмендегі Лагранж теоремасын айтуға болады.

Теорема 8. Егер G группасы шекті группа болса, онда

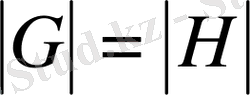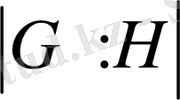
мұнда H ішкі группа, ал оның элементтерінің саны.

Салдар. Егер G группасының элементтерінің саны n натурал саны болса, онда оның кез келген ішкі группасының элементтерінің саны n натурал санының бөлгіш болады.

Анықтама. G группа, H ішкі группа. Егер G группасының кез келген x элементі үшін x H = H x қатынасы орындалса, онда H ішкі группасын G группасының нормальдық бөлгіші деп атаймыз да, оны H ► G түрінде жазамыз. Бірлікгруппа және G группасының өзі әрдайым G группасынан нормальдық бөлгіш. Егер H ішкі группасы G группасына нормальдық бөлгіш болса, онда әрдайым x ^-1 Hx = H орындалады, мұнда x G.

Анықтама. Егер a = x ^-1 bx , x G теңдегі орындалса, онда а және b элементтерін түйіндес элементтер деп атаймыз. Сонда төмендегі қатынастар орындалады:

( a b ) ^x = a ^x b ^x , ( a ^x ) ^y = a ^xy

Бұл теңдіктерді тексеруге болады. Егер A және B G группасының ішкі жиындары болса, онда A ^B ={ a ^b │ a A , b B } түрінде жазуды қабылдаймыз. Сонда H ішкі группасы G группасына нормальдық бөлгіш болуы үшін қажетті және жеткілікті шарт H ^G H болуы. Басқаша айтқанда H ішкі группасы G группасына нормальдық бөлгіш болу үшін қажетті және жеткілікті шарт: оның өзіне түйіндес ішкі группасымен бірдей болуы мұнда

H ^x = x ^-1 Hx = H , x G

Анықтама. G группасының өзінен және бірлік группадан басқа ішкі нормальдық бөлгіші болмаса, онда G группасын жай группасы деп атаймыз.

Мысал. Реті немесе элементтерінің саны жай сан болатын циклдік группа әрдайым жай группа болады.

Анықтама. G группа. H - ішкі группа. M G болсын, онда

N _H ( M ) ={ h │ h H , M ^h = M }

жиынын M ішкі жиынының H - группасындағы нормализаторы деп атаймыз.

Сөйлем 1. N _H ( M ) жиыны H - группасына ішкі группа болады.

Шындығында, x , y N _H ( M ) десек M ^x = M және M ^y = M болады.

Сонда 1) ( M ^x ) ^y = M ^y = M сондықтан ( x * y ) N _H ( M ) . Олай болса, N _H ( M ) жиынында көбейту амалы бар.

2) Топтау заңы бар

ЕгерMx=Mболса, ондаEquation. 3 =M. Сондықтанx-1Equation. 3NH(M) .
Me=M, сондықтанeNH(M), мұндаe-бірлік элемент

Сонымен сөйлем 1. Дәлелденді.

Сөйлем 2. H ішкі группасының G группасына нормальдық бөлгіш болуына қажетті және жеткілікті шарт N _G ( H ) = G .

Теорема 9. G группасының ішкі жиыны M . H ішкі группа. Сонда M жиынымен H - ішкі группасының элементтері арқылы түйіндес болатын ішкі жиындардың класының қуаты 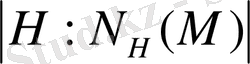индексіне тең, яғни

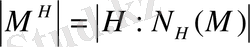
Ал жеке жағдайда

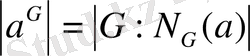
мұнда a ^G - a элементімен түйіндес болатын элементтердің жиыны.

Дәлелдеуі. N = N _G ( H ) деп алаыз. N - ішкі группасын N ішкі группасы бойынша оң іргелес кластарға бөлеміз, өйткені N H . Сонда Nx , x H , оң іргелес кластары пайда болады. M ^x жиынына сәйкес Nx лес класын қоямыз, яғни .

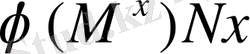Егер Nx = Ny болса, онда M ^x = M ^y болатыны түсінікті. Керісінше, егер M ^x = M ^y болса, онда Nx = Ny , себебі M ^N = M .

Егер Nx берілсе, онда оған сәйкес M ^x жиынынтабуға болады. Сондықтан, сәйкестігі жаба бейнелеу (отображение на ) болады. Сонымен, M ^x әртүрлі жиындарының класының қуаты 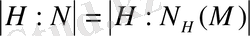болады. Енді x N , ал H=G , a=M десек 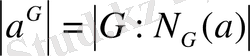теңдігі шығады. Теорема дәлелденді.