Комбинаторика мен ықтималдық теориясын оқыту әдістемесі және экономикалық қолданбалары


Мазмұны
І. Кіріспе . . .
ІІ. Негізгі бөлімі
2. 1. Қысқаша тарихы . . .
2. 2. Комбинаторика және ықтималдықтар теориясының негізгі ұғымдары
2. 2. Комбинаторика және ықтималдық теориясын оқыту әдістемесі . . .
2. 3. Комбинаторика мен ықтималдықтар теориясын қолданып
экономикалық мазмұны бар есептерді шығару әдістемесі . . .
ІІІ. Практикалық бөлім . . .
ІV. Пайдаланған әдебиеттер . . .
Кіріспе
Ықтималдық теориясы дегеніміз- жаппай кездейсоқ құбылыстардың математикалық моделі. Ықтималдық теориясының алғашқы ұғымдарын дүниеге келтірілген есептер сақтандыру істерін дамытуға байланысты пайда болған. Лоторея ойындары мен сақтандыру компанияларының өмірге келуі ықтималдық теориясының дамуына ықпал жасады. Күнделікті тұрмысымызда көптеген құбылыстар мен олардың өзгерістері кездеседі, солар оқиғаның тууына себепші болады. Мысалы, металл теңгені жоғары қарай лақтырсақ, ол жоғары көтеріліп барып, жерге түседі. Осы жасаған әрекетіміз сынақ немесе тәжірибе деп аталады. Жердегі металл теңгенің «елтаңба» немесе «цифр» жағының жоғары жатуы- оқиға болады. Сақамен тізілген асықтарды атқанымыз- сынақ болады. Сақаның тізілген асықтарға тиюі немесе мүлт кетуі оқиға болады. Бұл мысалдан оқиға сынақтың нәтижесі екенін, ал оқиға туғызу үшін сынақ жүргізу керек екенін аңғарамыз. Оқиғаларды латын алфавиті бас әріптерін пайдаланып белгілейміз: А, В, С, . . . Егер А оқиғасы әр сынақта сөзсіз пайда болса, онда ол ақиқат оқиға деп аталады. Сынақ кезінде пайда болмайтын оқиға мүмкін емес деп аталады. Сынақ кезінде пайда болуы да, пайда болмауы да мүмкін оқиға кез дейсоқ оқиға деп аталады.
Мақсаты: Заман талабына сай қазіргі техниканың- сенімділік, жаппай қызмет көрсетуі, автоматикалық басқару, өнім сапасын статистикалық бақылау теорияларды да ықтималдық теориясы көмегімен ықтималдық заңдылықтардың математикалық моделін құру арқылы іске асырылады.
Өзектілігі: Қазіргі кездегі ғылым мен техниканың ғарыштап өсу дәуірінде ықтималдықтар теориясының әдістері практиканың сан алуан салаларында кеңінен қолданып, физика, химия, биология құбылыстары, техника мен экономика процесстерінің заңдылықтарын жан-жақты және терең түсінуге орасан зор ықпалын тигізеді.
Болжам: ХХ ғасырдағы тибиғаттану ғылымының келбеті есептелетін кибернетиканың өзі ықтималдық теориясына негізделеді. Сондықтан кездейсоқ оқиғаның математикалық моделін жасаудың алғы-шарты үлкен сериялы сынақтарда кездейсоқ оқиға жиілігінің тұрақты болуына әкеледі. Олай болса, тәжірбиеден алынған нәтиже зауыттың технологиялық процестеріне байланысты заңдылықтарды көрсетеді, ол тек кездейсоқ құбылыстарға тән.
Нәтиже: Математикалық анализ әдістері бізді қоршаған реалды процестерді ықтималдық теориясынсыз толық суреттей алмайды. Сосын көпшілік жағдайда субъективтік ықтималдықтың дәлірек мәнін анықтау қосымша эксперименттің көмегімен шығарылады. Субъективтік ықтималдық туралы арнайы теориялар бар. Сондықтан субъективтік ықтималдықтың теорияларын дәрігерлер, психологтар қолданылады.
ІІ. Негізгі бөлімі
2. 1. Қысқаша тарихы
Әлемдегі кездейсоқ құбылыстар ерте заманнан бері зерттеліп келеді. Ол туралы Реньидің де жақсы пікірлері бар. Кездейсоқ құбылыстарға математикалық тұрғыдан қарау Паскаль мен Фермаға дейін болған. Демографиялық құбылыстар және адамдарды азық-түлікпен қамтамасыз жиілігінің біркелкілік фактілері Ежелгі Қытай мен Римде белгілі болған. Кездейсоқ құбылыстарды нақты әдістердің көмегімен анықтау мүмкіндігін Кордано мен Галилей де қарастырған.
Паскаль, Ферма және Гюйгенстен басап, кездейсоқ оқиға және оның ықтималдығы туралы математикалық ғылым- ықтималдық теориясының алғашқы ұғымдары қалыптаса бастады.
ХХ ғасырдың екінші жартысынан бастап құбылыстардың сандық өлшемдері әр түрлі процестердің, атап айтсақ, өндірісті математикалық модельдеу мен ғылыми шығармашылықтың алғашқы шарты болды, яғни ықтималдық ерекше маңызға ие болды. «Оқиға туралы ғылым» көптеген мамандық иелерінің: инженерлер, экономистер, дәрігерлер және әр түрлі шаруашылық саласындағы мамндардың ортасына енді. Бүкіл әлемде осы ғылымға қызығушылықтың артқаны соншалық, тіпті ықтималдық теориясы жиі қолданылатын болды деп айтсақ қателеспейміз.
Ықтималдық теориясының негізгі мағынасын ашып ықтималдықтың жиілік теориясының негізін салған белгілі неміс математигі- Р. Мизес (1883-1953) . Ол ықтималдық теориясын математика пәні емес, математикалық әдістерде кең қолданылатын ғылым қатарына қосты. Р. Мизес «Әр ықтималдыққа берілген есеп кейбір шынайы процестермен байланысқан», - деп айтқан. Қазіргі ықтималдық теориясының дамуы, әсіресе А. Н. Колмогоровтың еңбегінде, ықтималдық теория жоғары математикалық тарауларымен: жиын теориясы, функция теориясы, функционалдық талдау және т. б. нақты математикалық ықтималдықпен тығыз байланысқан.
Қазіргі ықтималдық теориясының әдістері қолданылмайтын сала жоқ. Ықтималдық статистика әдістерін қолдану көптеген ғылым салаларында дәстүрлі бағыт болуда. Оларға: физика, геодезия, өлшеу теориясы және т. с. с. жаады. Кейінгі кезде ықтималдық теориясын мединицина және биология, әскери ғылым мен космонавтика, лингвистика, психология теориясы мен оқыту теориясы, т. б. ғылымда да қолдана бастады. Одан басқа ықтималдық әдістерінің негізінде ықтималдық теориясынан шыққан жаңа ғылымдар қатары пайда болуда. Бұлар- ақпарат теориясы, сенімділік теориясы, сапаны статистикалық бақылау, тәжірибені жоспарлау.
2. 2. Комбинаторика және ықтималдықтар теориясының негізгі ұғымдары
ХХ ғасырдың 70-жылдарының соңынан бүгінгі күнге дейін қолданбалы математиканың маңызды бөлімдерінің бірі стохастика адам қызметінің барлық саласына кеңінен енуімен сипатталады. Ықтималдықтар теориясы мен математикалық статистиканың элементтерін байланыстыратын бұл ғылым физика, химия, биология, экология, геология, география, экономика, лингвистика, психология т. с. с. білімнің барлық салаларында қолданыс табуда.
Паскаль, Я. Бернулли, П. Лаплас тағы басқа ғалымдардың еңбектерінің нәтижесінде өмірге келген ықтималдықтар теориясы адам өмірінің әлеуметтік-мәдени, білім беру, ғылыми-өндірістік саласындағы кез-келген мәселені шешуде қолданылатын статистика ғылымының математикалық негізі болып табылады. Бұл мектеп курсында ықтималдықтар теориясы және математикалық статистика негізінің оқытылуының өзектілігін айқындайды.
Қазіргі мектептерді реформалау мектептегі математикалық білімнің мазмұнының өзгеруіне және математиканы оқыту әдістемесінде ықтималдық-статистиканы енгізудің қажеттілігінің мазмұнды-әдістемелік жағына көңіл бөлуге әкелді.
Ықтималдықтар теориясы және математикалық статистиканы оқытудың негізгі мақсаттары мынадай:
- өмірдегі нақты құбылыстарды дәл сипаттайтын стохастикалық модельдерін құру және зерттеу арқылы ықтималдықтар теориясы және математикалық статистика элементтерімен таныстыру.
- Ықтималдықтар теориясы және математикалық статистика курсы бойынша есептер шығаруда ықтималдықтық-статистикалық аспектісінің «қолданбалық» ойлау дағдысын дамыту.
- Ықтималдықтар теориясы аппараттарын қолдану негізінде оқушылардың математикалық мәдениеттілігін көтеру.
Ықтималдықтар теориясының математикалық аппараты оқушыларда қалыптасқан элементар математикалық білімге, дағдыға, ептілікке негізделгенін атап көрсетуге болады. Бұл кезеңде оқушылар нақты сандарға арифметикалық амалдар орындауды, функциялық символикаларды байыптап қолдануды, элементар геометриялық объектілер туралы түсінік қалыптасып, оларға операциялар жасауды біледі.
Сондықтан ықтималдықтар теориясы оқушыларға алған математикалық білімін нақты қолданатын, адам өмірінде маңызы зор математиканың бір тарауы ретінде қарастырылады.
Сыныптың бейінділігіне байланысты «Ықтималдықтар теориясы және математикалық статистика элементтері» тақырыбының оқытылуының математикалық абстракциялану деңгейі әртүрлі болуы мүмкін.
Ықтималдықтар теориясында «оқиға» ұғымы теориялық-жиын түсінігімен тікелей байланысты. Дербес жағдайда, анықтама бойынша «оқиға» деп элементар нәтижелер жиынының ішкі жиыны қарастырылады.
Сондықтан, бұл ұғымның анықтамасын нақты беру үшін, оқушылар жиындар теориясының элементтерімен, ықтималдықтар теориясының теориялық негіздерімен таныс болуы тиіс.
Жиындар теориясын оқыту мектеп курсында қарастырылмағандықтан, бұл мәселені шешу мұғалімнен үлкен әдістемелік шеберлікті талап етеді. Бастауыш мектептің математикасының экспериментальды курсын қолдану осы мәселенің бір шешімі болып табылады. Бастауыш мектепте жиын ұғымы интуитивті түрде қарастырылып, жиындарға қолданылатын амалдар мен олардың қасиеттері иллюстративтік (көрнекі) әдіс арқылы беріледі. 9-сыныптың «Алгебра» оқулығында «Ықтималдықтар теориясы элементтері» тарауы «жиын ұғымы» тақырыпшасынан басталады. Мұнда жиын ұғымына қысқаша түсінік беріліп, ішкі жиын, тең жиындар, шектеулі, шектеусіз жиындарға анықтама беріледі.
Жиындарға қолданылатын бірігуі, қиылысуы, айырымы амалдарына анықтама беріліп, белгілеулері ұсынылады. Жиындарға қолданылатын амалдарды Эйлер-Венн диаграммасы арқылы иллюстрациялаудың оқушы үшін маңызы зор. Сонымен қатар шектеулі жиындар үшін қосу, көбейту ережелерін меңгеру ықтималдықтар теориясының элементтерін оқуға үлкен ғылыми-әдістемелік даярлық болады. Осы ұғымдардың негізінде оқиға, оқиғаларға амалдар қолдану және олардың қасиеттері тақырыптарын оқыту мәселесі жеңілдетіледі.
Олай болмаған жағдайда мұғалім оқушыларды алдын-ала жиындар теориясының мәліметтерімен таныстыру арқылы бұл мәселені шешуде әдістемелік тұрғыдан орынды. Ықтималдықтар теориясының негізгі ұғымдарын оқытуда логикалық тұрғыдан қамтамасыз ету ерекше екенін атап айтуға болады. Мұнда жиындар теориясының қажетті ұғымдарының базасында (негізінде) ықтималдықтар теориясының негізгі ұғымдары енгізіледі. «Оқиға» ұғымын оқыту оқушыларда психологиялық тұрғыдан қиындықтар туғызады. Себебі оқушылар үшін «оқиға» ұғымы «тәжірибе» ұғымымен пара-пар.
«Оқиға» ұғымының қалыптасуы қарапайым ықтималдықтық модельдері қарастырудан басталады. Мысалы, тенгені лақтырсақ, ол жоғары көтеріліп барып жерге түседі. Бұл әрекет сынақ немесе тәжірибе деп аталады. Теңгенің «елтаңба» немесе «цифр» жағының жоғары қарап түсуі оқиға болады. Дәл осылайша, ойын сүйегін лақтыру, урнадан шар алу, нысананы дәлдеп ату - интуитивті денгейде «элементар тәжірибелер» ұғымын қалыптастырады. Бұл мысалдардан оқушылар оқиғаны тәжірибенің нәтижесі екенін, ал оқиға туғызу үшін тәжірибе, сынақ жүргізу керек екенін аңғарады. Оқушыларға оқиғалардың түрлетін - ақиқат оқиға, мүмкін емес оқиға, үйлесімді, үйлесімсіз оқиғалардың анықтамасын түсіндіруде күнделікті тұрмысымыздағы көптеген құбылыстардан мысалдар келтіру тиімді. Қарастырылған мысалдардың негізінде қос-қостан үйлеспейтін және тең мүмкіндікті элементар оқиғалардың жиыны ретінде «оқиғаның толық группасы» ұғымы қарастырылады. Осы ұғымдардың барлығы ықтималдық теориясының маңызды ұғымы «оқиға» ұғымының анықтамасын тұжырымдауға мүмкіндік береді. Орындалу мүмкіндігіне қарай оқиғаларды классификациялаудың оқушылар үшін дүниетанымдық маңызы зор. Бізді қоршаған ортада ақиқат, мүмкін емес және кездейсоқ оқиғалардан басқа оқиғалардың болмайтынын түсіндіру қоршаған ортаның ықтималдық моделіне сүйенеді. Мұндай модельдердің мысалдары физика, химия, география, биология, тарих т. б. пәндерден алынып, пәнаралық байланыс жүзеге асырылады.
Оқиғаларды классификациялаудың негізінде «ықтималдық» ұғымының қалыптасуы жатыр. Егер бір нақты оқиғаның орындалуының мүмкін немесе мүмкін еместігіне қандай да бір сандық мән сәйкес қойсақ, атап айтқанда әрбір ақиқат оқиғаға 1 санын, ал мүмкін емес оқиғаға 0 санын сәйкес қойсақ, онда әрбір кездейсоқ оқиғаға (0; 1) интервалынан бір нақты сан сәйкес келетіні түсінікті. Оқиғаның ықтималдығынан бұрын оқушыларға «оқиғаларға амалдар қолдану» тақырыбын өткен дұрыс. Бұл тақырыпта олар оқиғалардың арасындағы қатынасты, байланысты, қарама-қайшылықты меңгереді. Оқиғалар арасындағы қамту қатынасы (А
 В) мынандай сөз тіркестерімен анықталады: «А оқиғаның орындалуы В оқиғасын тудырады», «В оқиғасы А оқиғасының бөлігі болады». Осы қатынастың негізінде тең оқиғалардың анықтамасын логикалық түрде беруге болады. Оқиғалар арасындағы қатынас пен амалдарды Эйлер-Венн диаграммалары арқылы көрнекі түрде қолдану керек.
В) мынандай сөз тіркестерімен анықталады: «А оқиғаның орындалуы В оқиғасын тудырады», «В оқиғасы А оқиғасының бөлігі болады». Осы қатынастың негізінде тең оқиғалардың анықтамасын логикалық түрде беруге болады. Оқиғалар арасындағы қатынас пен амалдарды Эйлер-Венн диаграммалары арқылы көрнекі түрде қолдану керек.
Оқушылар теориялық жиын туралы түсініктерінің негізінде жиындарға және оқиғаларға қолданылатын амалдарды салыстырады. Оқиғалар мен жиындарға қолданылатын амалдардың анықтамаларындағы айырмашылық тек терминде ғана екеніне көз жеткізуге болады. Сондықтан жиындар теориясы мен ықтималдықтар теориясының терминдерінің сәйкестік таблицасын құру пайдалы.
Оқиғаларға амалдар қолдану және амалдардың қасиеттерін меңгеру оқушыларда ықтималдықтар теориясы курсының есептерін шығару дағдысын қалыптастыруда маңызы зор.
Ықтималдықтар теориясындағы тағы бір маңызды мәселе - элементар оқиғаларға амалдар қолдану нәтижесінде алынатын күрделі оқиға.
Егер мүмкін емес оқиғаға құр жиынды
 , ал ақиқат оқиғаға U жиынын сәйкес қойсақ, онда жиын теориясының теңбе-теңдіктерін ықтималдықтар теориясы тілінде тұжырымдауға болады. Мысалы, кез келген А оқиғасы үшін А
, ал ақиқат оқиғаға U жиынын сәйкес қойсақ, онда жиын теориясының теңбе-теңдіктерін ықтималдықтар теориясы тілінде тұжырымдауға болады. Мысалы, кез келген А оқиғасы үшін А
 U =А, А
U =А, А

 =
=
 , А
, А
 U =
U =
 , А
, А

 =А, А
=А, А
 А=А, А
А=А, А
 А=А, А
А=А, А

 , А
, А

 =
=
 теңдіктері ақиқат. Бұл теңдіктердің дәлелдеуін көрнекі түрде иллюстрациялап, мағыналы мысалдар келтіру арқылы түсіндіру қажет. Сонымен қатар, оқушыларға жаттығу жұмысы ретінде U
теңдіктері ақиқат. Бұл теңдіктердің дәлелдеуін көрнекі түрде иллюстрациялап, мағыналы мысалдар келтіру арқылы түсіндіру қажет. Сонымен қатар, оқушыларға жаттығу жұмысы ретінде U

 , U
, U

 , U \
, U \
 ,
,
 \ U өрнектерінің нәтижесін анықтауды ұсынуға болады.
\ U өрнектерінің нәтижесін анықтауды ұсынуға болады.
Оқиғаларға қолданылатын амалдарды оқытқанда сол амалдың мағынасын ғана анықтамай, оның басқа амалдардан айырмашылығын көрсететін мысалдарды көрнекі түрде қолдану керек. Оқушылар анықтамасы бойынша оқиғалардың қосуы мен көбейтіндісін оңай құрады. Осы материалға қосымша оқушыларды де Морган заңымен таныстыру қызықты болады.
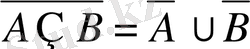 ,
,
 теңдіктерін Эйлер-Венн диаграммалары арқылы көрсету жеткілікті. Бұл заңды қарама-қарсы оқиғаны оқытуда қолдануға болады.
теңдіктерін Эйлер-Венн диаграммалары арқылы көрсету жеткілікті. Бұл заңды қарама-қарсы оқиғаны оқытуда қолдануға болады.
Оқиғаларға қолданылатын амалдардан кейін комбинаторика элементтерімен таныстырған дұрыс. «Комбинаторика элементтері» тақырыбы теориялық және қолданбалық тұрғыдан кең мағыналы болғандықтан «Ықтималдықтар теориясы» тақырыбынан бұрын да оқытуға болады.
Ықтималдықтар теориясының келесі негізгі ұғымы - ықтималдық. Бұл ұғымның да қалыптасуы «оқиға» ұғымын қалыптастырудағыдай жүргізіледі.
Қазіргі кезде «оқиға ықтималдығының» статистикалық, аксиомалық, классикалық, субъективтік анықтамалары белгілі. Мектеп курсында оқиға ықтималдығының статистикалық анықтамасы беріледі.
Кездейсоқ оқиғаның бір тәжірибе нәтижесінде пайда болатынын, немесе пайда болмайтынын алдын ала білу мүмкін болмағанымен, тәжірибені бірнеше рет қайталау барысында оның орындалуының белгілі бір заңдылығын байқауға болады. Бұл заңдылық оқушыларға таблица арқылы көрсетіліп, статистикалық тәсіл деп аталады.
Мектеп оқулығында «оқиғаның ықтималдығы дегеніміз - оқиғаның пайда болу мүмкіндігін білдіретін сан» деген анықтама беріледі. Осы санды анықтау үшін «салыстырмалы жиілік» ұғымы енгізіледі. Қандай да бір тәжірибе n рет қайталансын. Сонда қарастырылып отырған А оқиғасы m рет орындалсын.
 санын А оқиғасының салыстырмалы жиілігі деп атайды.
санын А оқиғасының салыстырмалы жиілігі деп атайды.
«Салыстырмалы жиілік» анықтамасын меңгеріп, осы ұғымды қалыптастыру үшін өмірден, өнеркәсіпбен, физика, химия, биология пәндерінен оқушыларға белгілі мысалдар қарастыру қажет. Мұндай мысалдарда қайталанған тәжірибе саны n=5, n=10, n=15 т. с. с болып келеді. Осындай аз көлемдегі ақырлы санды тәжірибелер барысында А оқиғасының орындалу саны m-ді есептеуге болады. Сонан соң оқиғаның салыстырмалы жиілігі
 санын табамыз. Осы ұғымды меңгергеннен кейін тәжірибе саны n өте үлкен болатын жағдайды қарастырамыз. Мысал ретінде өнеркәсіп орнының өндірілген өнімінің сапасын тексеру нәтижесінің кестесін құрайық.
санын табамыз. Осы ұғымды меңгергеннен кейін тәжірибе саны n өте үлкен болатын жағдайды қарастырамыз. Мысал ретінде өнеркәсіп орнының өндірілген өнімінің сапасын тексеру нәтижесінің кестесін құрайық.

Бұл кестеден тәжірибенің саны неғұрлым көп болған сайын салыстырмалы жиілік 0, 95 тұрақты санына жуықтайтынын көреміз. Сондықтан 0, 95 саны осы оқиғаның пайда болу мүмкіндігін көрсетеді. Осы сан анықтама бойынша оқиғаның ықтималдығы болады. Мектеп оқулығында «Сол тұрақты
 саны А оқиғасының ықтималдығы деп аталады да Р(А) деп белгіленеді» деген анықтама берілген. Сонда
саны А оқиғасының ықтималдығы деп аталады да Р(А) деп белгіленеді» деген анықтама берілген. Сонда
 саны әрі оқиғаның жиілігін, әрі ықтималдығын көрсетіп тұр. Ал осы екі ұғымның арасындағы үлкен айырмашылықты оқушыларға түсіндіру мұғалімнен үлкен әдістемелік шеберлікті талап етеді.
саны әрі оқиғаның жиілігін, әрі ықтималдығын көрсетіп тұр. Ал осы екі ұғымның арасындағы үлкен айырмашылықты оқушыларға түсіндіру мұғалімнен үлкен әдістемелік шеберлікті талап етеді.
Оқиға анықтамасын салыстырмалы жиілік арқылы бергеннен кейін, оның мынандай қасиеттерін оқушылар жеңіл меңгереді.
1. n рет тәжірибе жүргізгенде А оқиғасының орындалу саны
 болғандықтан салыстырмалы жиілік
болғандықтан салыстырмалы жиілік
 арақатынасын қанағаттандырады. Сондықтан
арақатынасын қанағаттандырады. Сондықтан
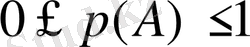 болады, яғни оқиғаның ықтималдығы [0, 1] сегментіндегі кез келген нақты санға тең бола алады.
болады, яғни оқиғаның ықтималдығы [0, 1] сегментіндегі кез келген нақты санға тең бола алады.
2. n рет тәжірибе жүргізгенде ақиқат оқиға m=n рет орындалады. Сондықтан оның ықтималдығы Р(U) =1.
3. Дәл осылайша, мүмкін емес оқиғаның ықтималдығы 0-ге тең екенін оқушы тез меңгереді.
4. Кездейсоқ оқиғаның ықтималдығын анықтағанда, тәжірибе қаншалықты көп жүргізілсе, оқиғаның жиілігі оның ықтималдығына соншалықты жақындайтынын мысалдар арқылы статистикалық тұрғыдан түсіндіру қажет.
Ықтималдық теориясы және матматикалық статистика ұғымдарын математика курсында кеңейтіп, жалпылау қажет.
Күнделікті өмірде қандай да бір оқиғаны бағалау нәтижесінде, дәл, нақты мағынасына мән берместен, «ықтималдық» ұғымын қолданып жүрміз. Мысалы, «50 пайыз ықтималдыпен», «
 ықтималдыпен» немесе «100-дің 50 жағдайы», «50-де 50», «екіден бір мүмкіндік» деген сөз тіркестерін толық түсініп, жайбарақат қабылдаймыз. Тиынды лақтырмай-ақ, елтаңба жағы мен цифрдың түссу мүмкіндігі бірдей, ал оқиға нәтижесі
ықтималдыпен» немесе «100-дің 50 жағдайы», «50-де 50», «екіден бір мүмкіндік» деген сөз тіркестерін толық түсініп, жайбарақат қабылдаймыз. Тиынды лақтырмай-ақ, елтаңба жағы мен цифрдың түссу мүмкіндігі бірдей, ал оқиға нәтижесі
 санына тең екеніне келісеміз. Мысалы, егер тиынды лақтыра отырып, әрбір лақтырудан кейін, айталық 800 рет лақтарылғаннан кейінгі нәтижені тіркеген кезде, елтаңба жағы 402 рет түскен болса, онда түсудің салыстырмалы жиілігін
санына тең екеніне келісеміз. Мысалы, егер тиынды лақтыра отырып, әрбір лақтырудан кейін, айталық 800 рет лақтарылғаннан кейінгі нәтижені тіркеген кезде, елтаңба жағы 402 рет түскен болса, онда түсудің салыстырмалы жиілігін
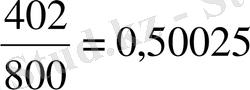 аламыз. Әрине, ол дәл
аламыз. Әрине, ол дәл
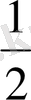 емес, бірақ оған өте жақын. Егер әрі қарай лақтыру (сынақ) санын көбейтсек, онда 402 санына жақынырақ санды алуға болар еді. Мұндай санның ықтимал болуы мүмкін.
емес, бірақ оған өте жақын. Егер әрі қарай лақтыру (сынақ) санын көбейтсек, онда 402 санына жақынырақ санды алуға болар еді. Мұндай санның ықтимал болуы мүмкін.
Сонымен, ықтималдық дегеніміз ─ белгілі бір анықталған жағдайда қандай да бір кездейсоқ оқиғаның пайда болу дәрежесінің сандық сипаттамасы.
Күнделікті өмірде бұл ұғымды жиі қолданамыз. Мысалы, бүгін мүмкін, кешігермін; ол мүмкін, бос емес шығар; жиналыстың болмауы мүмкін секілді.
Ықтималдық теориясы дегеніміз ─ кездейсоқ жағдайлардың пайда болу заңдылығын зерттейтін математикалық бөлігі.
Оқиғаның ықтималдығы дегеніміз ─ оқиғаның пайда болу мүмкіндігін білдіретін сан.
Кездейсоқ оқиғаның бір жолғы тәжірибеде пайда болатынын, не пайда болмайтынын алдын ала білуге мүкін болмағанымен, қайта-қайта жасалған тәжірибелер барысында, оның пайда болуының белгілі бір заңдылығы байқалады.
Белгілі жағдайда қайта-қайта
n
рет тәжірибе жасағанда
А
оқиғасы
m
рет пайда болса, онда
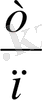 қатынасы А оқиғасы пайда болуының
салыстырмалы
жиілігі
деп аталады. Жоғарыдағы 5 бидай дәнін 5 тәжірибе, яғни m=4 деп ұғамыз. Сонда оқиғаның пайда болу жиілігі
қатынасы А оқиғасы пайда болуының
салыстырмалы
жиілігі
деп аталады. Жоғарыдағы 5 бидай дәнін 5 тәжірибе, яғни m=4 деп ұғамыз. Сонда оқиғаның пайда болу жиілігі
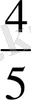 немесе 80% болады.
немесе 80% болады.
Сол тұрақты
 саны А
оқиғасының ықтималдығы
деп аталады да Р(А) деп белгіленеді.
саны А
оқиғасының ықтималдығы
деп аталады да Р(А) деп белгіленеді.
А және В оқиғаларының қосындысы деп А немесе В оқиғаларының кем дегенде біреуінің орындалатынын білдіретін оқиғаны айтады және оны А+В арқылы белгілейді.
Осыдан А+В-ның құрамына А-ға не В-ға тиісті элементтар оқиғалар енеді. Мысалы, ойын сүйегін тастағанда «жұп ұпай түсуі» мен «үштен кем ұпай түсуін» білдіретін оқиғаларды қосу қажет болсын. Онда
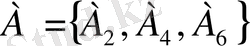 және В={А
1
, А
2
} оқиғаларын қосамыз: А+В={ А
2
, А
4
, А
6
}.
және В={А
1
, А
2
} оқиғаларын қосамыз: А+В={ А
2
, А
4
, А
6
}.
А және В оқиғаларының көбейтіндісі деп А және В оқиғаларының қатар орындалуын білдіретін оқиғаны айтады және оны А*В арқылы белгілейді. Сонымен, А*В-ның құрамына А-ға және В-ға да тиісті элементар оқиғалар енеді. Мысалы,
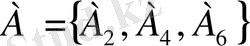 және В={А
1
, А
2
} оқиғалары үшін А*В={ А
2
} болады.
және В={А
1
, А
2
} оқиғалары үшін А*В={ А
2
} болады.
А және В оқиғаларының
айырмасы
деп тек А ғана орындалып, В-ның орындалмайтынын білдіретін оқиғаны айтады және оны А-В арқылы белгілейді. Осыдан А-В құрамына тек А-ға ғана енетін және В-ға тиісті емес элементар оқиғалар енеді. Мысалы,
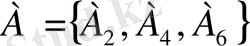 және В={А
1
, А
2
} оқиғалары үшін А-В={ А
2
, А
4
, А
6
} теңдіктері орындалады.
және В={А
1
, А
2
} оқиғалары үшін А-В={ А
2
, А
4
, А
6
} теңдіктері орындалады.
Егер А 1 , А 2 , . . . А п элементар оқиғалары үшін А 1 +А 2 + . . . +А п =U және A i *A j =Ø (i≠j) шарттары орындалса, онда бұл оқиғаларды элементар оқиғалардың толық тобы (группасы) деп аталады. Мысалы, ойын сүйегін тастағанда А 1 , А 2 , А 3 , А 4 , А 5 , А 6 элементар оқиғалары толық топ құрайды. Шынында да, ойын сүйегін тастағанда алты ұпайдың бірі түсері ақиқат, яғни А 1 +А 2 + А 3 + А 4 + А 5 + А 6 =U қосындысы- ақиқат оқиға. Сонымен қатар, бір тастағанда екі түрлі ұпай түсуі мүмкін емес, яғни A i *A j =Ø (i≠j) - жалған оқиға.
Егер В оқиғасы орындалған сайын А оқиғасы да орындалып отырса, онда А-ны В оқиғасының
салдары
деп атайды және оны былай белгілейді: В
 А. Мысалы,
А. Мысалы,
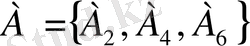 және С={ А
2
, А
4
} болса, онда А оқиғасы- С-ның салдары. Өзара кері А және
және С={ А
2
, А
4
} болса, онда А оқиғасы- С-ның салдары. Өзара кері А және
 оқиғалары үшін
оқиғалары үшін
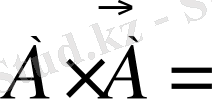 Ø және
Ø және
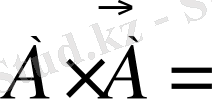 U теңдіктері орындалады. Кездейсоқ оқиғаларды жиындарға қолданылады:
U теңдіктері орындалады. Кездейсоқ оқиғаларды жиындарға қолданылады:
1 ─ Сурет Эйлер-Венн диаграммаларымен бейнелеген қолайлы.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz