Стохастикалық бағдарламалау негіздері: екі жақтылық әдісі, алғашқы базисті табу және тасымалдау әдістері


МАЗМҰНЫ
КІРІСПЕ
1. СТОХАСТИКАЛЫҚ БАҒДАРЛАМАЛАУ НЕГІЗДЕРІ
1. 1. Стохастикалық программалаудың екі жақтылық әдісі
1. 2. Стохастикалық программалаудың «солтүстік -батыс» бұрышы әдісі
1. 3. Ең кіші элемент әдісін пайдаланып алғашқы базисті табу
2. СЫЗЫҚТЫ ЖӘНЕ СЫЗЫҚТЫ ЕМЕС МОДЕЛІ
2. 1. Ағымдағы жоспарды тиімділікке тексеру мысалдары
2. 2. Қорларды басқарудың стохастикалық үлгілеулері
3. ҚОРЫТЫНДЫ
4. ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
5. ҚОСЫМША
КІРІСПЕ
Модель дегеніміз - нақты объектіні, процессті немесе құбылысты ықшам әрі шағын түрде бейнелеп көрсету.
Модельдеу - объектілерді, процесстерді немесе құбылыстарды зерттеу мақсатында олардың моделін (макетін) құру.
Модель - көрнекі түрде жазбаша жоспар, сызба ретінде жасалуы мүмкін. Мұндай модель барлық уақытта біздің ойымызда бейнеленетін прототип пайда болғанға дейін жасалады. Бір объект үшін әр түрлі модель жасалуы мүмкін. Модельдің жасалуы зерттеу мақсатына және прототип жөнінде жинақталған мәліметтердің көлеміне тәуелді болады. Мысалы, жуық арада басқа қалаға қыдырып баратын болдық делік. Ол қала туралы өзіміз білетін мәліметтерді жинақтап, ойымызды қорытып, қиялымызда сол қаланың моделін жасай бастаймыз. Мұндағы мақсатымыз - басқа қаламен танысу. Қаланы аралап келгеннен соң, толық мәлімет алғандықтан, ойымыздағы модель өзгеруі мүмкін. Ал сол қаланың сеулетші жасаған моделі мүлде өзгеше болады. Өйткені, оның мақсаты - үйлер мен ғимараттардың үйлесімді орналасуы, құрылысы және оларды көркейтіп қайта жаңарту болып табылады.
Модельдерді қасиеттеріне қарай мынадай топтарға жіктейді:
1. Қолдану аймағы.
2. Модельде уақыт факторын ескеру.
3. Білім саласына қарай топтау.
4. Модельді көрсету тәсіліне қарай топтау.
Қолдану аймағына қарай модель не үшін және қандай мақсатқа қолданылады деген сұраққа жауап беру мақсатында оқу, тәжірбиелік, ғылыми-техникалық, ойын, имитациялық тәрізді топтарға жіктеледі.
Оқу моделі - көрнекі оқу құралдары, әр түрлі машықтандырушы, үйретуші программалар түрінде болуы мүмкін.
Тәжірбиелік модель - жобалау объектісінің кішірейтілген немесе өте майда объектілер үшін олардың үлкейтілген көшірмесі болып табылады.
Ғылыми-техникалық модельдер - процесстер мен құбылыстарды зерттеу мақсатында құрылады. Оған мысал ретінде электрондардың жылдамдығын үдеткіш - синхротрон, найзағайдың разрядын бақылаушы құрал және теледидар тексеруге арналған стендтерді айтуға болады.
Модельді уақыт факторына байланысты динамикалық және статистикалық деп екі топқа жіктеуге болады. Статистикалық модель деп объект жөнінде алынған ақпараттың белгілі бір уақыт бөлігіндегі үзіндісін айтуға болады.
Динамикалық модель - уақыт барысындағы объектінің қасиеттерінің өзгерісін көрсету мүмкіндігін береді.
Экономика - математикалық модельдеуде көптеген есептер оптимизациялық болып табылады, яғни көзделген деп аталатын бірнеше функцияның максималды мәнін, шектелген аргументт арқылы табу. Мұндай есептерге: өнім өндіруде максималды пайданың шартын анықтау немесе жеткізуді минималды шығын шығатындай есеп жоспаралау мысал бола алды. Нақты есептердің көптеген шарты болады, сондықтан тиімді шешімді табу үлкен көлемдегі есептеулерді талап етеді.
Экономикалық есептердің көптеген кластары көзделген функцияның бірнеше айнымалыдан тұратын сызықтық функциядан құралған тиімді мәнін табуға әкеп соғады. Стохастикалық программалаудың өзара екі жақтылық есебі осы класқа жатады. Көптеген есептер функциялық жағынан стохастикалық болмағанымен, математикалық нұсқасы сондай болады. Оған мысал қаржыны және несиені тиімді таратудың есептері, кәсіпорындар арасындағы өндіріс, егін алқаптары, әр түрлі жұмысшыларға арналған механизмдерді белгілеу, күшейту және тағы да басқа стохастикалық есептер болады.
Осы курстық жобада, стохастикалық тапсырманың тиімді шешімін алу турлі әдістермен келтірілген.
1 СТОХАСТИКАЛЫҚ БАҒДАРЛАМАЛАУ НЕГІЗДЕРІ.
1. 1. Стохастикалық бағдарламалаудың өзара екі жақтылық әдісі
Математиканың көптеген салаларында екі жақтылық теоремалары деп аталатын теоремалар кездеседі. Олардың әрқайсысы берілген теорияның кез-келген тұжырымы белгілі-бір ережелер стандарты бойынша екінші бір тұжырым алуға мүмкіндік береді және біріншісінің дұрыстығынан автоматты түрде екіншісінің де дұрыстығы алынады. Екі жақтылық есебінің мысалдары стохастикалық бағдарлау есебінде де кездеседі.
Өзара екі жақтылық есебін сипаттайық. Бастапқы немесе І-ші есеп деген атпен стохастикалық бағдарлаудың қандай да бір болмасын есебі берілсін де шектеулер теңсіздіктер түрінде болсын. Сонымен
a 11 х 1 +а 12 х 2 + . . .
а 21 -х 1 +а 22 -х 2 + . . .
п белгісізді т теңсіздікте жүйесі мен сызықты форма
f = с 1 х 1 +с 2 х 2 + . . . + с„х„ (2)
берілсін.
(1) -ші жүйенің барлық теріс емес шешімдерінің ішінен (2) -ші форманы минимумдейтінін табу керек. Қойылған есеппен екінші бір есепті, яғни бастапқы есептен екі жақтылық байланыста болатын есепті қарастырайық. Оның қойылуы мынадай: т - белгісізі бар п теңдеулер жүйесі берілген:
а
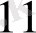 х
х
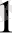 + а
+ а
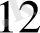 х
х
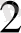 + . . . + а
+ . . . + а
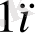 х
х
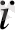 ≤ b
≤ b
 Equation. 3
Equation. 3
… … … … … … … …
a
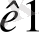 Equation. 3 x
Equation. 3 x
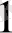 + a
+ a
 Equation. 3 x
Equation. 3 x
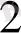 + … + a
+ … + a
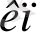 x
x
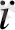 ≤ b
≤ b
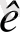
a
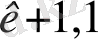 x
x
 + a
+ a
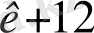 x
x
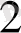 + … + a
+ … + a
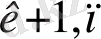 x
x
 = b
= b
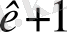
… … … … … … … …
a
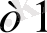 x
x
 + a
+ a
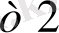 x
x
 + … + a
+ … + a
 x
x
 = b
= b
және стохастикалық форма
cр = b 1 у 1 +b 2 у 2 + . . . + b т у т
түрінде жазылады.
(Г) жүйесінің барлық теріс емес шешімдерінің ішінен (2') формасын
максимумдейтінін таңдап алу керек. Бұл есепті (П) - есеп деп алайық.
Екі есепті салыстыру арқылы мынаны байқауға болады.
1. Бастапқы есептегі белгісіздер жанындағы коэффициенттерден құрылған матрицасы мен екі жақтылық есебіндегі матрицалары бір - бірін «транспонирлеуден», яғни жатық жолды бағаналармен ауыстырудан алынады. Олардың реттері сақталады.
- Әр есептің шектеулер жүйесінің оң жағында екінші есептің сызықты формасының коэффициенттері орналасқан.
- Бастапқы есептегі теңсіздіктер > - типті, і-формасының минимумытабылу керек те, ал екі жақтылық есебіндегі шектеулерде < - типті теңсіздіктер, яғни қарама-қарсы мағыналы, алсрформасы максимум мэн, яғни қарсымағыналы мэн қабылдайды.
- Біреуінің белгісіздерінің саны, екіншісінің шектеулер санына тең.
- Осы бес шартты қанағаттандыратын стохастикалық бағдарлау есебі симметриялы деп аталады. Оның біреуі негізгі, ал екіншісі - екі жақтылы есептер деп аталады.
- Стохастикалық бағдарлау есептерінде симметриялы екі жақты парлармен қатар, симметриялы емес те екі жақты парлар кездеседі. Онда:
- а) Негізгі есеп: Теңдік сақталады:
а
 х
х
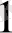 + а
+ а
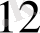 х
х
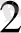 + . . . + а
+ . . . + а
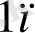 х
х
 ≤ b
≤ b
 Equation. 3
Equation. 3
… … … … … … … …
a
 Equation. 3 x
Equation. 3 x
 + a
+ a
 Equation. 3 x
Equation. 3 x
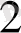 + … + a
+ … + a
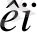 x
x
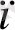 ≤ b
≤ b
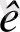
a
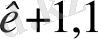 x
x
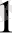 + a
+ a
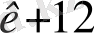 x
x
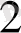 + … + a
+ … + a
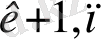 x
x
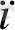 = b
= b
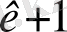
… … … … … … … …
a
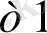 x
x
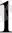 + a
+ a
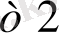 x
x
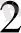 + … + a
+ … + a
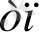 x
x
 = b
= b
б) Екі жақтылық есебі:
а
 у
у
 + а
+ а
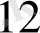 у
у
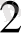 + . . . + а
+ . . . + а
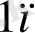 у
у
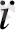 ≤с
≤с
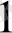 Equation. 3
Equation. 3
… … … … … … … …
a
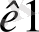 Equation. 3 у
Equation. 3 у
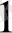 + a
+ a
 Equation. 3 у
Equation. 3 у
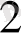 + … + a
+ … + a
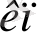 Equation. 3 у
Equation. 3 у
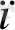 ≤ с
≤ с
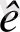 Equation. 3
Equation. 3
a
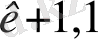 Equation. 3 у
Equation. 3 у
 + a
+ a
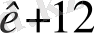 Equation. 3 у
Equation. 3 у
 + … + a
+ … + a
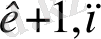 Equation. 3 у
Equation. 3 у
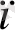 = с
= с
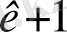 Equation. 3
Equation. 3
… … … … … … … …
a
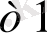 Equation. 3 у
Equation. 3 у
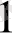 + a
+ a
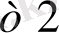 Equation. 3 у
Equation. 3 у
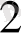 + … + a
+ … + a
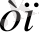 Equation. 3 у
Equation. 3 у
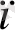 = с
= с
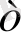 Equation. 3
Equation. 3
Бұл есептер симметриялы пар жағдайынан мынадай екі жолмен ерекшеленеді:
- (3) - (4) -ші есептердегі шектеулер теңдікпен берілген.
- (3') -(4') -\і = 1, т) теріс еместік
белгілері жоқ.
2. Сонымен қатар, екі жақтылық есебіндегі стохастикалық форма үшін
mах ср = -min (- ср)
- болатынын көрсетуге болады. Олай болса, екіншісі үшін екі жақтылық есебі, 1-ші есеппен бірдей болады, яғни симметриялы пардағы екі есеп, өзара екі жақты деп аталады.
Екі жақтылық теоремасы. Егер бастапқы есептің тиімді шешімі бар болса, онда екінші екі жақтылық есебінің де тиімді шешімі бар болады. Әрі / -формасының минимумы, ср -формасының максимумына тең болады.
тіп / = тах ф.
Егер бастапқы есепте стохастикалық форма төменнен шектелмеген болса, онда екі жақтылық есебінде шектеулер жүйесінің бірде-бір теріс емес шешімі болмайды.
Екі жақтылық әдісі
Екі жақтылық теоремасымен бағдарлау есебін шығарудың әдістерінің бірі «екі жақтылық әдісі» деп аталатын әдіспен байланысты. Оның мағынасы мынадай:
Стохастикалық бағдарлау есебі теңсіздік түріндегі шектеулермен берілсін. Оны біз Г-есебі ретінде қабылдайық та, ол үшін екі жақтылық есебі болып табылатын І-ші есепті құрып, оның шешімін симплекс-әдісті пайдаланып табайық. Бұл жағдайда екі жақтылық теоремасына мынадай қосымша енгізуге болады. Өзара екі жақты (I) жэне (II) есептері (1) -(2) жэне (1’) -(2') түрлерінде берілсін. Егер І-ші есепте біз бастапқы базистен тиімді базиске көшетін болсақ, ал одан кейін (II) есебіндегі сәйкес базистерді ауыстырсақ, онда (II) есебіндегі жаңа базис те тиімді болады. Әрі біреуінің базисті шешімі екі жақтылық есебіндегі стохастикалық формасының сәйкес базисті емес айнымалыларының жанындағы коэффициенттерінің теріс таңбамен алынған жаңа базистік айнымалыларына теңестіру арқылы алынады.
Сәйкестік былай орнатылады:
Х 1 Х 2 Х … Х п+т
. . .
Ут+1'" Ут+п У . . . Ут
Осылай тұжырымдау нәтижесінде (II) есебінің шешімі табылады. Екі жақты симплекс эдіске бастапқы есептегі шектеулер саны, айнымалылар санынан көп болған кезде қолдану ыңғайлы.
Мысал 1. ф = -у х - 2у 2 - Зу 3 - формасын максимумдеу қажет болсын жэне ол келесі шектеулермен берілген
- у, + 2у 7 -Зу. 1
2у -у 2 -у 3 <-1
Бұл қойылған есепті ІІ деп алдық. Оған екі жақтылық есебі болатын І-ші есепті құрайық. Ол былай қойылады:
f = x 1 - x 2 - формасын минимумдеу керек жэне ол төменгі шектеулермен жүйесімен берілген.
-х х + 2x 2 >-1
2x 1 - x 2 > -2
- 3x1 - x 2 > -3
Енді бұл форма мен шектеулердің қалай алынғанын түсіндірейік. Алдындағы келтірілген теория бойынша (1) -(2) жүйесі мен І"-формасы, (1') -(2') жүйесі және ср - формасымен мынадай байланыста болады.
ІІ есепте айнымалылар саны үшеу және де: с х = 1-ге, с 2 = - 1 - ге, т = 3 - тең. Теңдеудің саны екеу, ал жалпы түрде
ср = Ь х -у х +Ь 2 -у 2 + . . . + Ъ т -у т .
Салыстыру арқылы b х =\, b 2 =-2, b ъ =-3- терге тең және (Г) -тің бастапқы екі теңдеуінен
а п =-1, а 2Х =2, а ъх =-3, а п =2, а 22 =-1, а Ъ2 =-\. \ә
-екендіктеріне көз жеткіземіз.
Осы айтылғандарды пайдаланып І-есепті құрамыз.
/ = с х -х х +с 2 -х 2 + . . . + с п -х„ (2)
және (1) -ді табамыз. т = 3 - болғандықтан шектеулер жүйесі 3 теңдеуден тұруы керек.
с х = 1, с 2 = -2 - болып табылды, сондықтан
/ = \-х х +(-\) -х 2 =х х -х 2 .
Енді (1) -ші шектеулерді жазайық
х 2 >-1 (=b Х ) (2) -х 1+ (-\) -х 2 >-2 (=b 2 ) (-3) -х 1+ (-1) -х 2 >-3 (=b 3 )
- x1+ 2x2>-12x1- x2> -2
- 3x1- x2> -3
F = x 1 -х 2 .
- Шектеулер жүйесі және мақсатты функция алынды. Екі жақтылы есебі шықты. Жаңаданx3, x4, x5айнымалыларын қосу арқылы І-ші есепті мына
- түрде жазуға болады.
- 1-ші есеп.
- - x1+ 2x2- x3=-1
- -х5=-3
- Минимумдеу
- / =x1- x2+0 •x3+0 •x4+0 •x5
- және барлық
- айнымалылары теріс болмауы тиіс.
- Есепті симплекс-әдіспен шығаруға болады. Тек, есепті келесі түрге келтірген ыңғайлы
x 2 =2 + 2x 4 - x 5 ,
x 2 = 2 + 2x 1 - x 4 ,
f= x 4 - x 1
(II) - екінші қарастырылған есептің экономикалық мағынасына тоқталайық.
Ресурстары b г \і = \, т) өндіріс орны, бұл ресурстарды өнім шығару үшін
пайдаланады және оны өткізеді. Мұндағы қойылатын мақсат ресурстарды артық жұмсамай, өнім бағасын максимум пайда түсіретіндей етіп анықтау керек. Бастапқы (1) -(2) есебі теріс еместік шартымен қарама-қарсыға өзгерген түрінде алайық.
Ах<b, х>0, / тах =тах<с, х>, х у >0 (у=м) (3) берілсін.
мұндағы x } - } -ші түрлі өнім шамасы, С } - } -ші түрлі өнімнің бір
бірлігінің шамасы, а ц - } -ші өнім бірлігіне жұмсалатын / -ші ресурс шығыны.
Енді қандай бір болмасын өндіріс орны ресурстарын өнім дайындауға шығындамай-ақ, тікелей сатуға жіберуге үйғарды дейік.
Ресурсты қандай бағамен сату керек деген сұрақ туады?
Баға сатушыны да, сатып алушыны да қанағаттандыруы керек.
Сатып алушы ресурстар үшін неғұрлым аз төлегенді қалайды. Ал сатушы ресурстар үшін алғаны, бұрынғы дайын тауар үшін тапқан пайдасынан кем болмауын қалайды.
Есептің математикалық моделі
1. Мақсатты функция
- (р = b г у 1 + b 2 у 2 + . . . + b т у п -->mіп (4)
сатып алатын жақтың мақсатын сипаттайды. у т - /-ші ресурс бірлігінің бағасы.
2. Шектеулер жүйесі сатып алушылардың қызығушылығын сипаттайды.
Әр өнім бірлігін дайындауға кеткен ресурстарды бағалау қажет. Сонымен қатар ол ресурстар бағасын өткізілетін өнім бірліктері бағасымен шектеу керек
3. Баға теріс бола алмайды.
Уі >0 (і = \^п)
Сонда екі жақтылық белгісі негізгі есеппен жаңадан қойылған есептердің модельдерін салыстыру арқылы алынады.
Осы екі жақты есеп болудың бес белгісі бізде бұрын айтылған.
І - тура есеп, ІІ - оған екі жақтылық есебі.
Егер осы есептердің біреуінің стохастикалық функциясы шектеусіз болса, онда есеп қарама-қайшылы.
Екі жақтылықтың екінші теоремасы:
Теорема 2 . Егер тура есептегі стохастикалық функция шектеусіз болса, онда оның екі жақтылық есебінің шешімі болмайды.
Мысал 1.
Тура есеп.
f = 6x 1 + 4x 2 -» mах
2x 1 + 4x 2 < 8
2x 1 + x 2 < 6
Екі жақтылық есебі.
ср = 8x + 6x 2 -> mіп
2y + 2y 2 > 6
4у, +2у 2 >4
Екі жақтылық есебін құрудың мысалдары.
Мысал 1. Стохастикалық программалау есебі қойылған: cызықты функция
Ғ = 14x 1 +10х 2 +14х 3 +11х 4
келесі шектеулермен берілген.
4x 1 + 2x 2 + 2x 4 + 3x 4 < 35 x 1 +х 2 +2х 3 +3х 4 <30 3x 1 + x 2 + 2x 3 + x 4 > 40 x 1 >0, х 2 >0, х 3 >0, х 4 >0.
Қойылған есепке екі жақтылық есебін құрыңдар.
Шешуі: Есептің шешу жолын келесі кесте түрінде береміз.
Кесте 1
Мысал 2. Стохастикалық программалау есебі қойылған:
Ғ = 5x 1 - x 2 + 8x 3 - x 4 -^ тах
2x 1 + 5x 2 - x 3 + 7x 4 < 2,
- 5x3- x4> 3,
- 3x3+ 7x4< 5
- X
x 2
x 1 >0, х 2 >0, х 3 >0, х 4 >0.
Қойылған есепке екі жақтылық есебін құрыңдар Екі жақтылық есебіне тағы бір мысал қарастырайық. Мысал -3. Берілген стохастикалық бағдарлау есебіне
+10х 2 -» шіп
+3х 2 > 6 + x 2 > 9
I x - 8 x < 8
x 1 > 0, x 2 > 0
екі жақтылық есебін құрыңдар.
Шешуі: Келесі кестені құрайық.
Кесте 2
\ 3 -1 80 3 1 8 10 6 9 -8 Ғ
V )
1. 2 «Солтүстік -батыс» бұрышы әдісі
«Солтүстік -батыс» бұрышы әдісінде тасымалдау құндарының есепке алынбайтындығы белгілі. Сондықтан, Кесте -1-ді тасымалдау құндарысыз келтіреміз.
Кесте 3
Қадам -1 . (1, 1) -ұяшығын «солтүстік -батыс» бұрышы үшін қабылдаймыз. Қадам-2. Оған x" =min{і20, 60}=60-жүк бірлігін жеткіземіз.
Қадам -3.
1 ' =а г -х и =120-60
1' = Ъ } - х 1; = 60 -
60 = 0 - айырымдарын табамыз
Қадам -4 . Бұдан 1-ші тұтынушының сұранысы өтелгенін көруге болады. Кесте-2-нің 1-ші бағанының (1, 1) -ұяшығын тұтас сызықпен, қалған ұяшықтарды пунктермен ерекшелейміз де Қадам -1-ге көшеміз.
II. Қалған қадамдар бойынша әрекеттерге түсініктеме бермейміз.
- «с - б» бұрышы -(1, 2) .
- x12=шіп{б0, 100}=60
- а = 60-60 = 0, Й2= 100 -60 = 40
- 1-ші жолдағы қор бітеді. Оны қарастырудан алып тастаймыз.
III. 1. «с -б » бұрышы -(2, 2) .
- x22=шіп {70, 40} =40
- а2=70-40=30, й; =40-40 = 0
- 2 -ші бағананы қарастырудан шығарамыз.
IV. 1. «с - б» бұрышы -(2, 3) .
- x23=min{30, 80}=30
- а2=30-30 = 0, й; =80-30 = 50
- 2- ші жолды қарастырудан шығару керек. Бірақ, ол жол не сызылған, несандармен толтырылған.
V. 1. «с -б» бұрышы -(3, 3)
- x33=min{50, 50} =50
- а'3=Ь'3=0
- Кесте ұяшықтары бітті. Соңы.
Алынған жоспардың тасымалдау құнын есептейік. Ол үшін тасымалдау мөлшерін сол ұяшықтағы тасымал «с -б» бұрышы құнына көбейтеміз.
/ 0 = 60 • 5 + 60 • 10 + 40 • 6 + 4 • 30 + 50 • 0 = 300 + 600 + 240 +120 = 1260
1. 3. Ең кіші элемент әдісін пайдаланып алғашқы базисті табу
Алдыңғы жағдайдағыдай жалпы түсініктемелерге толық тоқталмай-ақ есептеу алгоритмдерін келтіреміз. Әдісті пайдаланып, шығару жолы бұрын келтірілген. Сонымен, бұл әдістегі ерекшелік әрбір ұяшықтардағы тасымалдау құндарының есепке алынатындығы. Әр есептеу кезеңдерін Рим цифрларымен белгілейік. Алдымен көлік қатынасы кестесін қайтадан құрамыз.
Кесте 4
I. Есепті шығаруды ең кіші элементтер орналасқан ұяшықтарды анықтаудан
бастаймыз.
1 . Ең кіші элементтер (3, 1), (3, 2) жэне (3, 3) ұяшықтарында орналасқан.
Мысалы: (3, 2) ұяшығын таңдап алайық.
2. x 32 =тіп{50, 100}=50
- а3=50-50 = 0, Ь'2=100-50 = 50
- 3-ші жолды қарастырудан ойша алып тастаймыз. (3, 2) ұяшығын тұтассызықпен, жолдың қалған ұяшықтарын пунктир сызықтармен ерекшелейміз.
II. 1. Қалған кесте ұяшықтарының ішінен - (2, 3) -те ең кіші элемент
орналасқандығы көрініп тұр.
- x23=шіп {70, 80} =70
- а2=70-70 = 0, Ь'3=80-70 = 10
- Сарқылуына байланысты екінші жолды қарастырудан алып тастаймыз.
III. 1. Ең кіші элемент (1, 1) ұяшығында.
- хп=шіп{і20, 60} =60
- а[= 120-60 = 60, *; =0.
- Бірінші бағананы қарастырудан ойша шығарамыз. 1-ші өтелді.
IV. 1. Ең кіші элемент (1, 2) ұяшығында.
2. x 12 =шіп{б0, 50}=50
- а[=60-50= 10, Ь'2=0.
- Ағымдағы кестеде бір ғана (1, 3) ұяшығы қалады. 3 -ші өтелді. (1, 2) ұяшығын тұтас сызықпен ерекшелейміз.
V. 1. Соңғы (1, 3) ұяшығын таңдаймыз.
- x13=шіп{Ю, 10}=10
- а[=Ь'3=0
- Кесте сарқылды. Есептеу аяқталды. Барлық тұтынушылар қажеттіліктеріөтелді.
Табылған тасымал құны
/ жэ = 60 • 5 + 50 • 10 +10 • 12 + 70 • 4 + 50 • 0 = 300 + 500 +120 + 280 = 1200
Алдыңғы «солтүстік -батыс» бұрышы эдісімен салыстырғанда 60 бірлікке алғашқы жоспардың кемігенін көреміз.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz