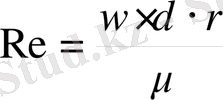Сұйық қозғалысының негіздері: жылдамдық, Бернулли, Рейнольдс және құбырлардағы гидравликалық кедергілер


Мазмұны
Кіріспе
Гидродинамикада - сұйық қозғалысының жалпы заңдары зерттеледі. Сұйықтар қозғалысының қоғаушы күші - қысымдар айырмасы болады. Қысымдар айырмасы насостармен, компрессорлардың жәрдемімен және сұйықтардың деңгейлері мен тығыздықтарының айырмасы арқылы пайда болады.
Гидродинамиканың заңдары берілген мөлшердегі сұйықты қажетті жылдамдықпен тасымалдау керек болған қысымдар айырмасын, яғни осы қозғалысқа жұмсалатын энергия шамасын, немесе керісіншө, берілген қысымдар айырмасы арқылы сұйықтың жылдамдығын және мөлшерін анықтауга мүмкіндік береді.
Гидродинамиканың сұйықтардың құбырлар мөн каналдар ішіндегі қозғалысын қарастырады және сұйықтардың әртүрлі денелерді (меха- никалық араластыру, қатты денелердің сұйықта тұнуы, т. б. ) толқындап ағуының заңдылықтарын қарастырады.
Кейбір процесстер, мәселен, сүзу, насадкалы аппараттардағы массаалмасу, реакторлардағы қатты катализатор арқылы өтетін химиялық процесстер және т. б. сұйықтардың күрделі пішіндегі каналдар ішінде қатты денелерде ағыстап қозғалуы гидродинамиканың аралас мәселесі болады.
Мұндай мәселелерді зерттегенде, мәселені ішкі және сыртқы деп есептеп, солар үшін шамалап шешеді.
І Бөлім. Сұйықтардың қозғалысының негізгі сипаттамалары
- Сұйықтың жылдамдығы және мөлшері
Сұйықтың көлденең қимасы тұрақты болған құбыр ішіндегі қозғалысын қарастырамыз.
Ағынның көлденең қимасы арқылы уақыт бірлігінде өткен сұйық шамасын, сұйықтың мөлшері деп атайды. Бұл мөлшердің м 3 /с немесе м 3 /сағ
пен өлшенетін көлемдік жәнө кг/с немесе кг/сағ. өлшенетін массалық түрлері болады.
Ағынның көлденең қимасының әртүрлі нүктелерінің жылдамдығы әртүрлі: құбыр қабырғасына жақын жерде ең аз, ал құбыр осінде ең көп болады. Көп жағдайларда жылдамдықтың көлденең қимасындағы үлесу заңы белгісіз және оны анықтау өте қиын. Сондықтан, есептеуде шындық /локальдік/ жылдамдықты емес, жалған орташа жылдамдықты қабылдайды. Бұл жылдамдық W (м/с) арқылы белгіленеді. Және ол сұйықтың көлемдік мөлшерінің V c (м 3 /с) көлденең қима ауданының S (м 2 ) қатынасына тең:
W= V c / S
бұл жерден көлемдік мөлшер:
V c = W S ( )
массалық мөлшер G кг/с былай анықталады:
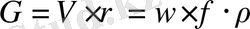
Мұндағы - сұйықтың тығыздығы, кг/м 3
W (кг/м 2 с) - массалық жылдамдық деп аталады.
Құбырларды есептеуде, тамшылы сұйықтардың, газ және булардың жылдамдықтарының мәндері қандай болу керектігін төменде қарастырамыз.
- Гидравликалық радиус және эквивалентті диаметр
Егер сүйықтар көлденең қимасынын пішіні дөңгелектен өзгеше болған қималар арқылы қозғалса, онда есепті ұзындық размер орнына гидравли-калық радиус немеее эквивалентті диаметр қабылданады. Сұйық ағатын құбырдың немесө каналдың көлденең қима ауданының сұйықтану периметріне қатынасы гидравликалық радиус деп аталады:
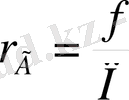
Мұнда f - cұйық ағынының көлденең қима ауданы
П - сұйықтану периметрі м/ құбырдың немесе каналдың сұйықпен шектелетін периметрі
Егер құбыр қимасы дөңгелек болса, және сұйық құбырмен толып ақса, онда
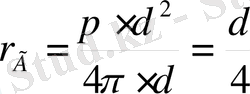
Гидравликалық радиус арқылы өрнектелген диаметр эквивалентті диаметр деп аталады:
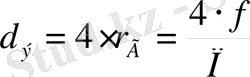
Сұйықтар қозғалысының режимдері .
Сұйық қозғалысының екі түрлі режимі туралы алғаш рет тәжірбие жүргізіп толық зерттеу жасаған ағылшын физигі О. Рейнольдс (1883 ж. ) болатын. Рейнольдстің қозғалыс рөжимін зерттеген қондырғысының схемасы 1- суретте келтірілген.
Сұйық деңгейі тұрақты болып тұратын ыдысқа (I) шыны құбыр қосылған. Сұйық мөлшерін реттеу үшін шыны құбырға кран (3) қойылған, Шыны құбырдың осі арқылы кішкене (2) түтікпен бояу жіберген.
1 -сурет. Рейнольдс тәжірибесін дәлелдеу үшін жасалған қондырғы
Шыны құбырдағы сұйықтың төменгі жылдамдықтарында бояу жан-жағындағы сұйықпен араласпай, шыны құбыр ішінде түзу сызық бойымен горизонталь жіп сияқты созылып ағады. Себебі, төменгі жылдамдықта сұйықтың бөлшектері бір-бірімен араласпастан, бір-біріне параллель, тартіпті түрде ағады. Мұндай қозғалысты ламинарлық режим деп атайды.
Егер кранды (3) көбірек ашса, қозғалыс жылдамдығы көбейгенде бояу сызықтын түзулігі бірден бұзылады. Бояу сызық, әуелі иреңдеп, соңынан басқа сұйық массасымен араласып, жоқ болып кетеді. Сұйықтың, мұндай белгісіз және бейберекетті траекториясымен және тәртіпсіз қозғалысын турбуленттік қозғалыс деп атайды.
Сұйық қозғалысының режиміне сұйықтың тұтқырлығы, тығыздьіғы, орташа жылдамдығы және құбырдың (каналдын) эквивалентті диаметрі әсер ететіні Рейнольдс тәжірбиелері арқылы белгілі болды. Бұл келтірілгеи төрт шамаларды біріктіріп, сұйықтардың қозғасының режимін анықтайтын бір өлшемсіз комплекс сан алуға болады:
Бұл комплексті Рейнольдс саны деп немесе критериі атайды.
Рейнольдс критериі тұтқұрлық күші мен қзғалыстағы ағынның инерция арасындағы күш қатынасының мөлшері болады
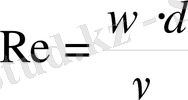
Ламинарлық режимнен турбуленттік режимге ауысу Рейнольдстін аумалы санымен сипатталады. Мәселен, сұйықтардың түзу тегіс құбырлар арқылы қозғалысында Re = 2320. Егер 2320 аз болса ламинар режимі, ал 2320 көп болса турбуленттік режим болады. Re > 1 болғанда орнықты турбуленттік режим болады. Re 2320 бен 1 аралығында орнықсыз турбуленттік немесе өтпелі режимі болады, себебі құбырда екі түрлі режим (кұбыр осінде турбуленттік, ал қабырға жанында ламинярлық) болуы мүмкін .
Рейнольдстің аумалы саны құбырдың бұдырлығына, пішініне және т. б. байланысты болады.
Ламинарлық қозғалыстағы сұйық жылдамдығының ағын қимасы бойын-ша таралуы.
Радиусы R түзу құбырдағы сұйықтың ламинарлық ағысын қарастырамыз. Бұл сұйық ағынынан ұзындығы l және радиуеы r болатын цилиндрлі қабатты бөліп аламыз. -сурет . Цилиндрдің екі көлденең шеткі беттеріне Р, Р 1 қысым күштері, ал оның бүйір бетінө үйкеліс күші Т әсер етеді.
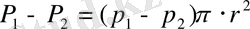
Р 1 және Р 2 - гидростатикалық қозғалыс
Цилиндрдің қозғалуына ішкі үйкеліс күші Т кедергі жасайды:
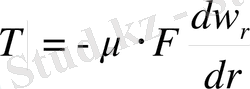 (1. 1)
(1. 1)
мұндағы w r - сұық қозғалысының жылдамдығы r;
F - цилиндрдің сыртқы беті тең 2π⋅r⋅l
Сурет 2. Стокс заңын еспептеуге арналған
Қысымдардың Р 1 және Р 2 айырмасы тұрақты қозғалыста үйкеліс күшін ауыздықтауға кетеді және бұл күштердің суммасы нөлге тең болу керек. Үйкеліс күші сұйықтық қозғалуына кедергі жасайды, сондықтан ол қысым айырмасына қарама қарсы бағытта болады:
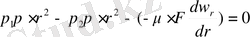
несесе
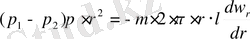
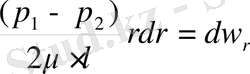
Құбырдағы сұйықтың барлық көлеміне көше отырып бұл дифферциальды теңдеуді интегралдаймыз, онда r радиусы r=R дейін, ал w=w r жылдамдығы w=0 дейін өзгереді
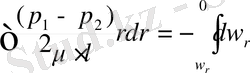
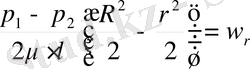
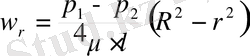 (1. 2)
(1. 2)
Әлбетте
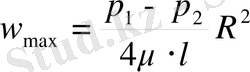 егер r=0
егер r=0
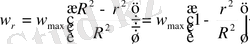 (1. 3)
(1. 3)
Алынған теңдеу Стокс заңы деп аталады. Онда ламинарлық қозғалыста құбыр қимасында жылдамдықтар парабол тәрізді таралады.
Ламинарлық қозғалыстағы сұйықтықтың шығынын есептеу үшін ішкі радиусы r сыртқы радиусы (r+dr), аумағы dF=2π⋅rdr болатын жәй сақиналы қиманы қарастырайық.
Осы қима арқылы өтетін сұйықтың көлемдік мөлшері тең:
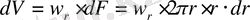
wr мағынасын орнына қоя отырып мынаны аламыз:
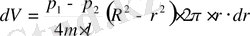
Интегралдаймыз:

Енді R орнына d=2R құбыр диаметрін қойсақ онда мынаны аламыз:
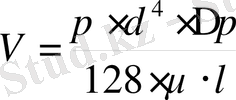 (1. 4)
(1. 4)
Дөңгелек құбыр бойынша ламиарлық қозғалыспен ағатын сұйықтың шығынын анықтайтын теңдеу Пуазейля теңдеуі деп атайды.
Көлемдік шығындарды салыстыра отырып w және w max арасындағы қатынастарды алуға болады:
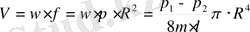
Бұдан
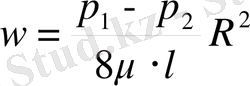 ( 1. 5)
( 1. 5)
Алынған өрнекті w max өрнегімен салыстыра отырып мынаны шығарамыз:
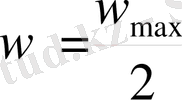 (1. 6)
(1. 6)
Сонымен құбырдағы ламинарлық ағында сұйықтың орташа жылдамдығы осі бойынша жылдамдықтың жартысына тең болады.
Өнекәсіптік тәжірибеде турбуленттік қозғалыс кең таралған. Турбуленттік қозғалыста бөлшектердің хаосты қозғалысынан ағынның негізгі массасында жылдамдықтардың теңдесуі байқалады және олардың таралуы құбыр қимасымен (айырмашылығы формасы параболдан болатын) қисықтықпен сипатталды.
Тәжірибе көрсеткендей турбуленттік режим қозғалысында жылдамдық w жартылай болмайды, ол одан едәуір көп, яғни 0, 8 - 0, 9 w max . Рейнолдс критериі неғұрлым көп болса ағынның жылдамдығы соншама жоғары болады.
- Бернулли теңдеуі
Тұрақты ағын үшін қозғалыстың Эйлер қозғалысының теідеуін шешу гидродинамиканың ең маңызды теңдеуі Бернулли теңдеуіне әкеледі.
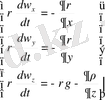 Эйлер теңдеуі
Эйлер теңдеуі
Теңдеудің сол және оң жағын тиісті
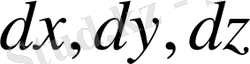 көбейтіп және
ρ бөлсек онда:
көбейтіп және
ρ бөлсек онда:
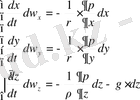 (1. 7)
(1. 7)
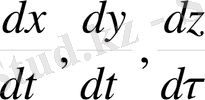 - тиісті остегі жылдамдық проекциялары, сондықтан, аталған теңдеулерді қосамыз:
- тиісті остегі жылдамдық проекциялары, сондықтан, аталған теңдеулерді қосамыз:
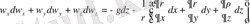 (1. 8)
(1. 8)
Теңдеудің сол жақ косындыларды былай жазуға болады:
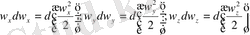
әлбетте, қосындысы:
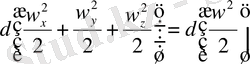 (1. 9)
(1. 9)
Қосылатын оң бөлімін төмендегідей көрсетуге болады:
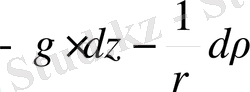
яғни:
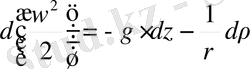
Екі бөлімін g бөліп , төмендегіні аламыз:
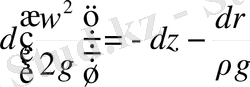 (1. 10)
(1. 10)
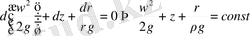 (1. 11)
(1. 11)
Алынған өрнек Бернулли теңдеуі деп аталады.
Кез келген көлденеі қима үшін былай жазуға болады:
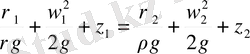 (1. 12)
(1. 12)
Мұндағы шаманы
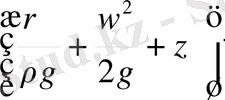 толық гидродинамикалық тегеурін деп аталады, сондықтан тұрақты ағынды идеалды сұйықтың гидродинаикалық тегеуріні тұрақты болады.
толық гидродинамикалық тегеурін деп аталады, сондықтан тұрақты ағынды идеалды сұйықтың гидродинаикалық тегеуріні тұрақты болады.
Теңдеудің оң жағында реальді газдар үшін жоғалған тегеурін h n.
1. 4. Бернулли теңдеуін тәжірибеде қолдану.
Бернулли теңдеуі іс жүзінде сұйықтардың жылдамдығы мен мөлшерін анықтау үшін. Мұндай мақсатта пневмоөлшеуіш түтіктер мен дроссельдер пайдалынады. Пневмо өлшеуіш түтіктермен сұйықтың жылдамдығы мен шығыны құбырдың осінде жататын, оның қима нүктесіндегі жылдамдық тегеурінің h ск деңгейінің айырмашылығын болады. h ск
арқылы құбыр бойындағы ең көп (максимальді) жылдамдықты анықтайды. Сондықтан, орташа жылдамдық сұйық ағынының режиміне байланысты.
Бұл әдіс қарапайым болғанымен пневмо өлшегішті құбырдың бойына орналастыру қиын болғандықтан дәл емес.
Сұйықтардың жылдамдығы мен мөлшерін анықтау үшін кең таралған дроссельді құрал жабдықтар, ал оларға өлшегіш диафрагма, вентури құбыры, өлшегіш сопло жатады.
Бұл құрал жабдықтардың принципі көлденең қималардың өзгеруіне байланысты қысымның айырмасына негізделеді.
Өлшегіш диафрагма, ортасы құбырдың осіне сәйкес келетін кішкене дөңгелек тесігі бар жұқа диск, құбырға бекітіледі.
Өлшегіш сопло сұйыққа кіретін жағы жатық иілеп, ал шығатын жағы кеңейіп келетін құрал.
Вентури құбыры алдымен біртіндеп тартылып, сосын біртіндеп құбырдың диаметріне дейін кеңейетін құбыр. Осындай пішініне байланысты мұндағы қысым шығыны өлшегіш өлшегіш диафрагма және соплоға қарағанда аз.
Вентури құбырында және соплода қысылған ағынның қима ауданы
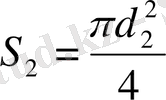 ;
;
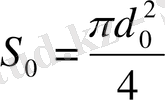 - тесіктің қима ауданы;
- тесіктің қима ауданы;
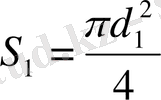 - дроссель приборы қойылған қиманың ауданы. Диафрагма жағдайында
- дроссель приборы қойылған қиманың ауданы. Диафрагма жағдайында
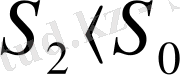 .
.
Екі қима үшін Бернулли теңдеуін былай жазамыз:
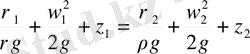
... жалғасы
(1. 13)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz