Тасымалдау есебін шешу

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 20 бет
Таңдаулыға:

Жоспар

Кіріспе3

Негізгі бөлім. 4

1 Тиімділік есептерінің модельдері4

2. Сызықты теңдеулерге арналған есептердің мысалдары6

3. Екі айнымалысы бар сызықтық теңдеулердің графикалық шешімдері8

4. Тасымалдау есебін шешу. 11

5. Тиімділік есебнің программасын құру және компьютер көмегімен тасымалдау есебін шешу мысалдары21

Қорытынды31

Кіріспе

Қазіргі кезде тасымалдау, машина жасау, ауыл шаруашылғы мен өнеркәсіп өнімдерін шығару салаларында экономикалық тиімді әдістерді қолдану маңызды орын алып отыр. Барлық салаларда оптимизациялау әдістерін қолдану кеңінен тараған, оны қолдану экономикалық маңызды мәселелерді шешу үшін жаңа математикалық модельдерді ойлап табу және ол есептерді шешу қажеттілігі туындайды. Математика саласында шешім қабылдау және жақсы нәтижеге жетудің тиімді жолдарын табу мәселесі алдыңғы қатарға қойылған. Осындай мәселелерді шешу үшін сызықты және сызықты емес программалау, ойындар теориясы, бұқаралық қызмет көрсету және т. б. теориялар қолданылады.

Тиімді әдістерді табу есептері сан алуан, мұндай мәселелерді тасымалдау есебін қолдана отырып шешуге болады. Тасымалдау есептерінің тиімді шешімдерін сызықты программалау арқылы симплекс-әдісімен шешуге болады. Әрине, тасымалдау есебін шығаруға осы мақсат үшін жасалған арнайы алгоритмдерді қолданған қолайлы. Жалпы алғанда тасымалдау есебі жүкті қамтасыз етушіден тұтынушыға дейін ең аз шығынмен жеткізудің жоспарын анықтайды. Дегенменен, тасымалдау есебінің математикалық модельдерін экономиканың басқа да көптеген салаларында қолданады.

Қазіргі кезде әр түрлі тасымалдау есептерін шығарудың көптеген алгоритмдері жасалған: үлестіру әдісі, потенциалдар әдісі, дельта-әдіс, венгер әдісі, дифференциалдау ренті әдісі, түрлі жүйелік әдістер және т. б. бұл әдістер былайша қарағанда жай есептер болып есептеледі. Бұл есептер әр түрлі қосымша шарттарға байланысты күрделене береді, мысалы есептегенде тасымалдау шығынымен қатар өнімнің өзіндік құнын ескеретін болсақ. Сондықтан, математикалық модельдер тасымалдауға жатпайтын көптеген факторларды есепке алуға мүмкіндіктер береді.

Сызықты программалаудың математикалық аппаратының негізін салған академик Кантарович Л. В. және оның бастауымен Кемчинов В. С, Новожилов В. В., Федоренко Н. П., Оганбарян В. Т т. б ғалымдардың жұмыстары арқасында бұл саланың әдістері кең қолданысқа ие болды. Атап айтсақ, энергетика, көлік, металлургия, ауылшарушылық, әскери іс салаларындағы экономикалық мәселелерді шешу осы әдістерге негізделеді.

Әр түрлі процесстерді сипаттау үшін математикалық модельдер жасалады, мысалы дескраптивтік мәселесі туындағанда басқа модель қажет болады. Басқару, тасымалдау, өнім шығару және т. б. процестерін сипаттау үшін тиімділік модельдерін қолданған жөн.

Тиімділік моделінің жалпы құрылысын қарастырайық.

Негізгі бөлім.

1 Тиімділік есептерінің модельдері

Алдымен бір процесті немесе бір құбылысты басқаруда қандай әрекет жақсы нәтижеге, қандай әрекет нашар нәтижеге жеткізетіндігін салыстыруға тоқталайық және бұл әрекеттердің нәтижелерін сапалық тұрғыдан бағалап қана қоймай, сандық нәтижелерін салыстыру мүмкін деп болжайық.

Берілген процесті не құбылысты М математикалық модель арқылы өрнектейік. Бұл модель - процесс қадамын анықтайтын параметрлер арақатынастарының жиынтығы болсын. X параметрлерінің ішінде U -басқару айнымалыларының жиыны болсын.

Әрбір әрекетті сандық нәтижесін бағалауға болатын болса, әрбір U басқаруға тәуелді Ф(U) санын анықтайтын Ф функциясы белгілі болсын.

Белгілі бір мақсатқа бағытталған әрекет - жақсы нәтижеге жетуді көздейді. Сондықтан барлық U -лардың ішінде Ф(U) мәнінің максимал мәні болатындай (mахФ( u ) =Ф( u ) ), не минимал мәні болатындай (mіnФ( u ) = Ф( u ) )

u $\in U$ $\in U$ u $\in U$ $\in U$

барлық u -ларды қарастырайық.

Мұндай есеп экстремалды немесе тиімділік есеп деп аталады. Бұл есеп М модельге және Ф(U) функциясына байланысты, сәйкесінше оптимизациялық есебін шешудің әдістері әртүрлі болуы мүмкін.

Барлық ғылымдар сияқты, экономика ғылымы да мынадай сұрақтарға жауап іздейді: Не өндіру керек? Қалай өндіру керек? Өнімнің өзіндік құны қандай болуы керек? Шығындарды қалай есептеу керек? және т. б.

Экономикалық мәселелердің шешу жолдары қандай болатыңдығын түсіну үшін келесі есепті қарастырайық. Ауылшаруашылық саласында жердің қандай ауданында, қандай дақылдар егу керек, мал шаруашылығы мен құс шаруашылығын қаншалықты іске асыру керек деген мәселені зерттейік.

Ең алдымен негізгі факторларды атап өтейік: жер көлемі, дақылдың өнімділігі мен қажеттілігі, ет, сүт, жұмыртқа өнімдеріне сұраныс, мал шаруашылығы мен құс шаруашылығына баспана, жем және т. б. өнімдермен қамтамасыздығы т. с. с.

Экономиканың кез келген саласында осындай мәселелер туындап отырады. Мәселелерді шешуге әсерін тигізетін факторлардың ішінде әсері ең жоғары болатын факторларды бөліп алған жөн.

Айталық, біз қарастырып отырған есепте осындай факторларды бөліп алдық дейік. Енді не істеу керек? Ендігі кезекте осы факторлардың әсерін бақылайық. Мысалы, мал бірлігін көбейтетін болсақ, мал оларды ұстайтын қораларды кеңейту мәселесі туындайды. Қандай да бір дақылдың өнімділігі жоғары болса, бұл дақылдың өндірісінен неғұрлым жоғары пайда көруді қарастыру керек т. с. с.

Бұл сұрақтарға жауап беру үшін маңызды факторларды сандық, сапалық түрде бағалайтын математикалық модель құрылады. Сандық бағалау - мақсат функциясымен беріледі.

2. Сызықты теңдеулерге арналған есептердің мысалдары

Есеп 1. Цех екі түрлі трансформатор өндіреді. Бірінші түрдегі
трансформатордың біреуіне 5 кг трансформаторлық темір мен 3 кг сым,
екінші түрінің бір трансформаторына 3 кг темір мен 2 кг сым жұмсалады.
Бірінші түрдегі трансформатордың біреуінен цехтың көретін пайдасы 1, 2 теңге болса, екіншісінен 1 теңге пайда көреді. Егер цехта 480 кг темір мен 300 кг сым бар болса, цех трансформатордың әр түрінен қаншасын шығарғанда көбірек пайда көреді?

х ₁ және х ₂ сәйкесінше бірінші және екінші түрдегі трансформатордың саны болсын. Трансформатор шығару үшін 5х ₁ + 3х ₂ кг темір мен 3x ₁ +2 х ₂ кг сым қажет. Барлығы 480 кг темір мен 300 кг сым болғандықтан келесі теңсіздіктер орындалуы керек.

5х ₁ + 3х ₂ $\leq$ $\leq$ 480

3х ₁ +2 х ₂ $\leq$ $\leq$ 300

Теңсіздік белгісі цехтың темір мен сымның барлығын жұмсау мүмкіндігінен қойылып отыр. Цехтың екі трансформатордың түрінен көретін пайдасы z=1, 2х ₁ +х ₂

Осы екі айнымалылы сызықты функцияның ең үлкен (максимал) мәнін табу керек. Мүндағы х ₁ жэне х ₂ мәндері келесі теңсіздіктер жүйесін қанағаттандыруы қажет:

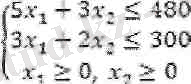
Соңғы х ₁ $\geq 0,$ $\geq 0,$ х ₂ $\geq$ $\geq$ 0 теңсіздіктері есептің мағынасына байланысты қойылып отыр. Себебі өндірілетін трансформатор саны теріс санмен белгіленбейді.

Есеп 2. Фермадағы малды қоректендіру үшін оларға күнделікті А қоректік затынан 33 бірліктен, В қоректік затынан 23 бірліктен, С қоректік затынан 12 бірліктен кем емес болатындай жем дайындалады. Сонымен бірге әрбір қоректік затта үш түрлі жем бар, олардың салмақтық үлестері келесі кестеде көрсетілген:

А: А

В: В

С: С

1массалық бірліктің бағасы: 1 массалық бірліктің бағасы

: 1 жем

: түрі

: массалық

А: 4

В: 3

С: 1 бірл

1массалық бірліктің бағасы: 20 теңге

: бірлікте

А: бірл

В: бірл

С: 1 бірл

1массалық бірліктің бағасы: 20 теңге

: 2 жем

: түрі

: массалық

А: 3

В: 2

С: 2 бірл

1массалық бірліктің бағасы: 10 теңге

: бірлікте

А: бірл

В: бірл

С:

1массалық бірліктің бағасы:

: 3 жем

: түрі

: массалық

А: 2

В: 1

С:

1массалық бірліктің бағасы:

: бірлікте

А: бірл

В: бірл

С:

1массалық бірліктің бағасы:

А, В, С қоректік заттарының қажет мөлшерімен қамтамасыз етілетіндей қоректің неғұрлым арзан болатын түрі қандай болады?

х ₁ , х ₂ және х ₃ арқылы 1, 2, 3 жем түрлерінің көлемін белгілейік.

А, В, С, қоректік заттарының көлемі төмендегі теңсіздіктерді

қанағаттандырады:

4х ₁ +3х ₂ + 2х ₃ $\geq$ $\geq$ 33

3х ₁ + 2х ₂ + х ₃ $\geq \$ $\geq \$ 23

х ₁ +х ₂ +2х ₃ $\geq$ $\geq$ 12

Ал күнделікті қоректің бағасы z=20х ₁ +20х ₂ +10х ₃ функциясымен анықталады.

Есептің мағынасы бойынша х ₁ $\geq$ $\geq$ 0, х ₂ $\geq$ $\geq$ х ₃ $\geq$ $\geq$ 0 екендігін ескере отырып, осы функцияның ең кіші (минимал) мәнін есептеу керек, ал х ₁ , х ₂ , х ₃

мәндері келесі теңсіздіктер жүйесін қанағаттандыруы керек:

4х ₁ +3х ₂ + 2х ₃ $\geq$ $\geq$ 33

3х ₁ + 2х ₂ + х ₃ $\geq \$ $\geq \$ 23

х ₁ +х ₂ +2х ₃ $\geq$ $\geq$ 12

х ₁ $\geq$ $\geq$ 0, х ₂ $\geq,$ $\geq,$ х ₃ $\geq$ $\geq$ 0

Жоғарыда қарастырылған есептер өздерінің мазмұны бойынша оптималдық есеп болып табылады. Мұндай есептерді сызықты программалау қарастырады. Дәлірек айтсақ, сызықты программалау - бұл бірнеше айнымалысы бар сызықты функцияның максимал немесе минимал мәнін есептеумен айналысатын математикалық сала. Сонымен бірге функцияның айнымалылары белгілі бір сызықты теңсіздіктер немесе теңдеулер жүйесін қанағаттандыратындай шарт қойылады.

Ең кіші немесе ең үлкен мәні есептелетін функция мақсат функциясы деп аталады. Ал айнымалылар қанағаттандыратын жүйе шектеу жүйесі деп аталады. Бірінші есепте мақсат функциясы z=1, 2х ₁ +х ₂ болса, шектеу жүйесі:

5х ₁ +3х ₂ $\leq$ $\leq$ 480

3х ₁ +2х ₂ $\leq$ $\leq$ 300

х ₁ $\geq$ $\geq$ 0, х ₂ $\geq$ $\geq$ 0

Анықтама 1. Шектеу жүйесінің кез келген шешімі сызықты программалау есебінің мүмкін болатын шешімі деп аталады.

Мысалы: 1- есептегі шектеу жүйесінің шешімі х ₁ =20, х ₂ = 60. Бұл 1-есептің мүмкін шешімі.

Анықтама 2. Мақсат функциясы максимал (минимал) мәніне жететіндей мүмкін шешім есептің оптималды шешімі деп аталады.

Сызықты программалаудың барлық есептерін екі түрге жіктеуге болады. Мақсат функциясының минимал мәнін табу есебі минимизациялау есебі деп аталады. Мақсат функциясының максимал мәнін есептеу қажет болса, мүндай есепті максимизациялау есебі деп атайды.

Алайда mаx z = - min (- z) екендігін ескерсек, кез келген максимизациялау есебін минимизациялау есебіне келтіруге болады және керісінше.

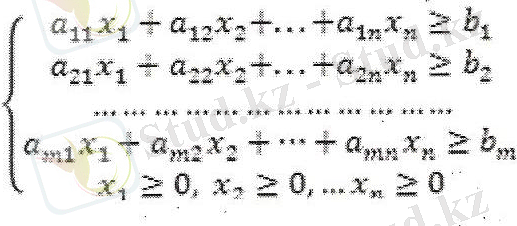Жалпы жағдайда оптимизациялау есебі келесі түрде анықталады. Айнымалылар саны n болса,

шарттарын қанағаттандыратындай х ₁ х ₂ , . ., х _n белгісіздері арасында z=c ₁ x ₁ + c ₂ x ₂ +…+ c _n функциясының ең үлкен (ең кіші) мәніне жететін мәндерін табу керек.

3. Екі айнымалысы бар сызықтық теңдеулердің графикалық шешімдері

Екі айнымалысы бар сызықты программалау есебі келесі түрде қарастырамыз:

a ₁₁ х ₁ + a ₁₂ х ₂ $\ \geq \$ $\ \geq \$ b ₁

a ₂₁ х ₁ + a ₂₂ х ₂ $\ \geq \$ $\ \geq \$ b ₂

a _n1 х ₁ + a _n2 х ₂ $\ \geq \$ $\ \geq \$ b _n

шарттарын қанағаттандыратындай х _ь х ₂ белгісіздері арасында z=c ₁ x ₁ +c ₂ x ₂ функциясының ең үлкен (ең кіші) мәніне жететін мәндерін табу керек.

Шектеу жүйесі сызықты теңсіздіктерден тұратын болғандықтан, оның шешімдер жүйесі координаталық жазықтықтың бірінші ширегінде жататын М дөңес көпбұрыш болып табылады.

Осыған байланысты есептің қойылуын өзгеше айтуға болады: М дөңес көпбұрышының барлық нүктелері арасында z=c ₁ x ₁ + c ₂ x ₂

Сызықты функциясының ең үлкен (ең кіші) мәніне жеткізетін нүктесін табу керек.

Егер z = d мәнін тұрақты етіп алсақ, онда екі белгісізі бар теңдеу пайда болады:

с ₁ х ₁ + с ₂ х ₂ = d. Бұл теңдеудің шешімдері координаталық жазықтық бойындағы түзудің нүктелері болып табылады. d-ның мәндерін - $\infty$ $\infty$ -ден + $\infty$ $\infty$ -ке дейін өзгертсек, бұл түзу, параллель көше отырып, бүкіл координаталық жазықтық бойын басып өтеді

(1-сурет) .

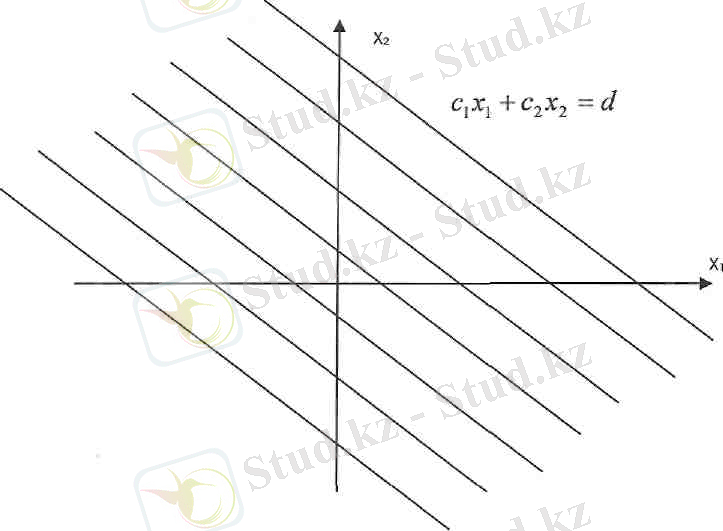
1- Сурет.

М дөңес көпбұрышы шектеу жүйесінің шешімі болсын. Онда d-ның мәндері - $\infty$ $\infty$ -ден + $\infty$ $\infty$ -ке дейін өзгерсе, онда с _х х _х +с ₂ х ₂ = d түзуі қайсыбір d= d ₁ мәніде М дөңес көпбұрышына жетіп, ортақ А нүктесінде басып өтеді. Бұл нүктені кіріс нүктесі деп атайық. Сонымен М көпбұрышын одан әрі баса өте отырып, қандай да бір d = d ₂ мәнінде соңғы ортақ В нүктесінен жанап өтеді. Бүл нүкте шыгыс нүктесі деп аталады

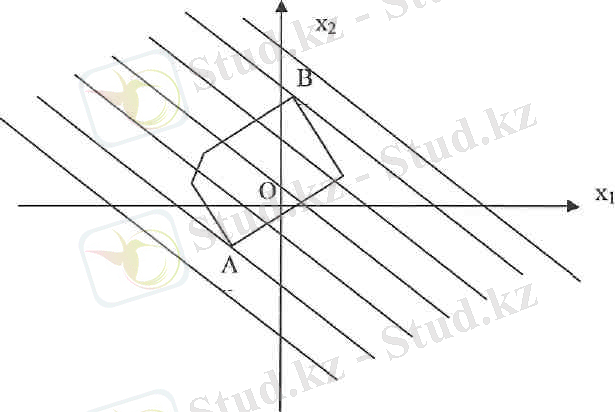
2-сурет.

Кейбір жағдайда с ₁ х ₁ +с ₂ х ₂ =d, түзуі көпбұрыштың бір қабырғасымен беттесуі

мүмкін (3-сурет)

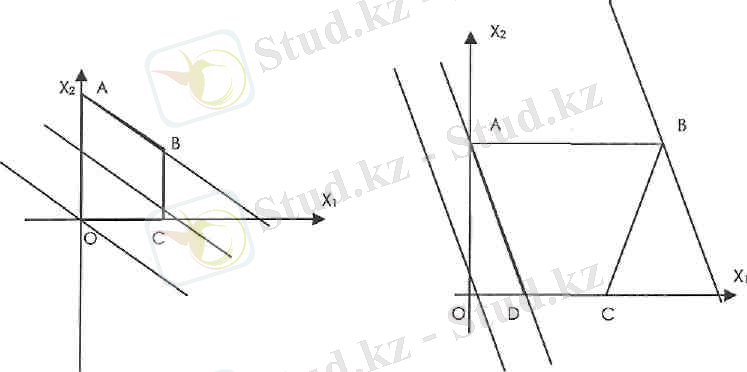
3-сурет 4-сурет

Бұл М көпбұрышында с ₁ х ₁ +с ₂ х ₂ =d түзуіне параллель қабырғалар болған жағдайда орындалады. Мақсаттық функция өзінің максимал (минимал) мәнін осы қабырғаның барлық нүктелерінде қабылдайды.

Осылайша 3-суретте мақсат функциясының максимал мәні АВ қабырғасымен, ал 4-суретте минимал мәні АБ қабырғасымен беттеседі.

Жүйенің мәндер жиыны ашық облыс болған жағдайда с ₁ х ₂ +с ₂ х ₂ = d түзуі d-ның мәндері - $\infty$ $\infty$ -ден + $\infty$ $\infty$ -ке дейін өзгерсе, шығыс (кіріс) нүктесін қабылдамауы мүмкін (5-сурет)

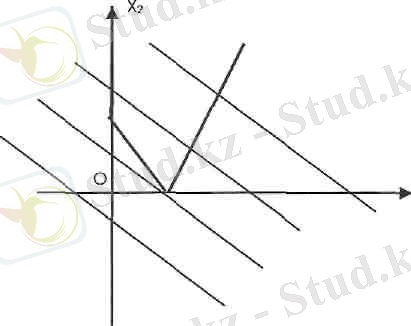5-сурет.

Бұл жағдайда мақсаттық функция максимал мәнге жетпейді.

Мақсаттық функция максимал (минимал) мәнге шығыс (кіріс) нүктесінде жететін болғандықтан, сызықты программалаудың есебін графикалық жолмен шешуді келесі жоспар бойынша орындау керек:

Шектеу жүйесінің мәндер облысын координаттар жүйесінде көрсету, мақсаттық функция түзуін тұрғызып, оны параллель көшіре отырып, шығыс немесе кіріс нүктесін анықтап алу, осы нүкте координатын анықтап, мақсаттық функцияның бұл нүктедегі мәнін анықтау керек.

Алдыңғы тараудың 1-есебінде мақсаттық функция z=1, 2х ₁ +х ₂ , ал шектеу жүйесі:

5х ₁ +3х ₂ $\leq$ $\leq$ 480

3х ₁ +2х ₂ $\leq$ $\leq$ 300

х ₁ $\geq$ $\geq$ 0, х ₂ $\geq$ $\geq$ 0

мұндағы 5х ₁ +3х ₂ $\leq$ $\leq$ 480 теңсіздігін а деп, ал 3х ₁ +2х ₂ $\leq$ $\leq$ 300 теңсіздігін в түрінде белгілейік. Осы есептің графикалық бейнесі келесі 6-суретте көрсетілген.

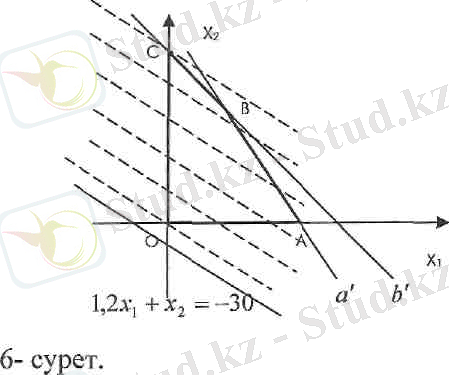
Мұнда алдымен шектеу жүйесінің АВСО көпбұрышын тұрғызамыз. Сонан соң z = 1, 2х ₁ + х ₂ мақсат функциясына мән бере отырып, мысалы z = -30 деп алып, 1, 2х ₁ + х ₂ = -30 түзуін түрғызамыз. Сонан соң ол түзуді параллель көшіре отырып, шығыс нүктесінің С нүктесінде болатындығын анықтаймыз. С нүктесі в теңсіздігін бейнелейтін b' түзуі мен Ох ₂ түзулерінің қиылысу нүктесі. Оның координаттары

3х ₁ +2х ₂ =300

х ₁ =0

теңдеулер жүйесінен табылады. Бүл жүйенің шешімі: х, = 0, х ₂ = 150.

Сонымен мақсат функциясының ең үлкен мәні z=1, 2 ^. 0+150 =150, ол х ₁ =0, х ₂ =150 мәндерінде қабылданады.

4. Тасымалдау есебін шешу.

А ₁ , А ₂ , А ₃ үш станциясынан сәйкесінше а ₁ , а ₂ , а ₃ тонна жүгін В ₁ , В ₂ , В ₃ және В ₄ станцияларына жеткізу қажет. B ₁ пунктіне b ₁ тонна, В ₂ -ге b ₂ , В ₃ - ге b ₃ , ал В ₄ пунктіне b ₄ тонна жүгін жеткізу қажет. Әрі А _i (і = 1, 2, 3) станцияларындағы барлық жүктің массасы В _j (j = 1, 2, 3, 4) пункттеріне жеткізуге қажетті жүктің салмағына тең: а ₁ + а ₂ + а ₃ = b ₁ +b ₂ +b ₃ +b ₄

Кез келген А _i (i = 1, 2, 3) станциясының біреуінен В _j (j = 1, 2, 3, 4) пунктінің кез келгеніне бір тонна жүкті жеткізуге кететін қаражат белгілі, ол келесі кестеде көрсетілген:

В1: В ₁

В2: В ₂

В3: В ₃

В4: В ₄

: А ₁

В1: с ₁₁

В2: с ₁₂

В3: с ₁₃

В4: ^С ₁₄

: А ₂

В1: ^С ₂₁

В2: с ₂₂

В3: с ₂₃

В4: с ₂₄

: А ₄

В1: с ₃₁

В2: ^С ₃₂

В3: с ₃₃

В4: с ₃₄

1 - Кесте

(с шамасының 1-ші индексі жүк шығатын станцияның номері, ал 2-ші индекс жеткізу пунктінің номерін білдіреді. )

Бұл есепте келесі шарттар орындалатындай тасымалдау жоспарын құру қажет:

1) В ₁ , В ₂ , В ₃ және В ₄ пунктеріне жеткізуге қажетті жүкті түгелімен

жеткізу;

А1, А2, А3станцияларындағы жүкті түгелімен жеткізу;
жалпы тасымалдауға кететін шығындар аз жұмсалуы қажет.

Айталық х _у (і = 1, 2, 3; / = 1, 2, 3, 4) деп А. _i станциясынан В _j пунктіне жеткізілетін жүк массасын белгілейік. Сонда барлық белгісіздер саны 12 болады:

х ₁₁ , х ₁₂ , х ₁₃ , х ₁₄ , х ₂₁ , х ₂₂ , х ₂₃ , х ₂₄ , х ₃₁ , х ₃₂ , х ₃₃ , х ₃₄ ,

Есептің берілгені мен белгісіздерді келесі кестеде көрсетейік:

Шығу станциялары

Жүк салмағы

Жеткізу пунктері мен жеткізуге қажетті жүк салмағы қажетті

В ₁

b ₁

В ₂

b ₂

В ₃

b ₃

В ₄

b ₄

Шығу станциялары: А ₁

Жүк салмағы: а ₁

Жеткізу пунктері мен жеткізуге қажетті жүк салмағы қажетті:

с ₁₁

х ₁₁

с ₁₂

х ₁₂

с ₁₃

х ₁₃

с ₁₄

х ₁₄

Шығу станциялары: А ₂

Жүк салмағы: а ₂

Жеткізу пунктері мен жеткізуге қажетті жүк салмағы қажетті:

с ₂₁

х ₂₁

с ₂₂

х ₂₂

с ₂₃

х ₂₃

с ₂₄

х ₂₄

Шығу станциялары: А ₃

Жүк салмағы: а ₃

Жеткізу пунктері мен жеткізуге қажетті жүк салмағы қажетті:

с ₃₁

х ₃₁

с ₃₂

х ₃₂

с ₃₃

х ₃₃

с ₃₄

х ₃₄

2-кесте

Сонда мақсат функциясы келесі түрде беріледі:

z $= с$ $= с$ ₁₁ х ₁₁ + $\ с$ $\ с$ ₁₂ х ₁₂ + $\ с$ $\ с$ ₁₃ х ₁₃ + $\ с$ $\ с$ ₁₄ х ₁₄ + $\ с$ $\ с$ ₂₁ х ₂₁ + $\ с$ $\ с$ ₂₂ х ₂₂ + $\ с$ $\ с$ ₂₃ х ₂₃ + $\ с$ $\ с$ ₂₄ х ₂₄ + $\ с$ $\ с$ ₃₁ х ₃₁ + $\ с$ $\ с$ ₃₂ х ₃₂ + + $с$ $с$ ₃₃ х ₃₃ + $\ с$ $\ с$ ₃₄ х ₃₄

қысқаша түрде:

\[z=\sum_{i=1}^{3}\stackrel{4}{\mathcal A}_{i}\mathrm{}~~c_{i j}x_{i j}\]

\sum_{\begin{array}{r} \\ i = 1 \end{array}}^{3}{\sum_{j = 1}^{4}с_{ij}}

х_{ij}

Мақсат функциясы тасымалдауға жұмсалатын шығындарды білдіреді.

$\geq$ Есептің мағынасына сәйкес х _ij $\geq$ 0 ( i = 1, 2, 3; j= 1, 2, 3, 4) . Ал шектеу жүйесі келесідей беріледі:

$\geq 0$
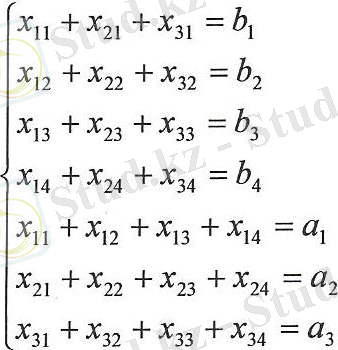
Осы жүйені қанағаттандыратын және мақсат функциясының мәнін ең кіші мәніне жеткізетін х _ij $\geq 0$ мәндерін табу керек.

Тасымалдау есебінің шешу жолын 3 қадамда жүргіземіз.

2-ші кестедегі а ₁ мен b ₁ мәндерін сандық мәндермен алмастырып

жазайық:

Шығу станциялары

Жүк салмағы

Жеткізу пунктері мен жеткізуге қажетті жүк салмағы қажетті

В ₁

300

В ₂

500

В ₃

100

В ₄

200

Шығу станциялары: А ₁

Жүк салмағы: 100

Жеткізу пунктері мен жеткізуге қажетті жүк салмағы қажетті:

с ₁₁

х ₁₁

с ₁₂

х ₁₂

с ₁₃

х ₁₃

с ₁₄

х ₁₄

Шығу станциялары: А ₂

Жүк салмағы: 400

Жеткізу пунктері мен жеткізуге қажетті жүк салмағы қажетті:

с ₂₁

х ₂₁

с ₂₂

х ₂₂

с ₂₃

х ₂₃

с ₂₄

х ₂₄

Шығу станциялары: А ₃

Жүк салмағы: 600

Жеткізу пунктері мен жеткізуге қажетті жүк салмағы қажетті:

с ₃₁

х ₃₁

с ₃₂

х ₃₂

с ₃₃

х ₃₃

с ₃₄

х ₃₄

3-кесте

1-қадам. Базистік шешімдерді табу.

х _ij тасымалдауларын табу үшін келесі әдісті қоладанайық. Ол үшін А ₁ мен В ₁ торындағы х ₁₁ тасымалдауын белгілейік. В ₁ ге қажетті жүк салмағы 300, А ₁ -дегі жүк салмағы 100, олардың кішісін х ₁₁ -ге теңестіреміз: х ₁₁ =100. Бұл мәнді кестеге толтырып, с ₁₁ -ді қоршап қояйық. Енді х ₂₁ -ді анықтайық. А ₂ -дегі жүк салмағы мен В ₁ -ге жеткізуге қажетті жүк салмағын салыстырайық. А ₂ -дегі жүк салмағы - 400, В ₁ -ге жеткізуге қажетті жүк салмағы -200, олардың кішісі 200, оны х ₂₁ -дің орнына жазамыз, с ₂₁ -ді қоршап қоямыз. В ₁ -ге жеткізуге қажетті жүк салмағы толығымен қамтамасыз етілді. Олай болса келесі тік торларды қарастырамыз, ол А ₂ мен В ₂ торы. А ₂ -дегі қалған жүк салмағы 200, В ₂ -ге жеткізуге қажетті жүк салмағы 500, оларды салыстырсақ, кішісі 200, оны х ₂₂ -нің орнына толтырамыз да, с ₂₂ -ді қоршап қоямыз. А ₂ -дегі жүктің барлығы жұмсалғандықтан, оны қарастырмаймыз. В ₂ -ге қажетті жүк салмағы 500, оның 200-і х ₂₂ мәніне теңестірілді, олай болса қалған 300-і х ₃₂ - нің орнына толтырылады. А ₁ , А ₂ торлары толып қойған, олай болса соңғы жолдардың қалғанын толтырамыз: х ₃₃ = 100, х ₃₄ =200. с ₃₂ , с ₃₃ , с ₃₄ мәндерін қоршап қоямыз.