Анықталған интеграл

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

Жоспары:

І. Кіріспе

ІІ. Негізгі бөлім

* Анықталмаған интеграл анықтамасы

* Анықталмаған интегралдың қасиеттері

* Анықталған интеграл анықтамасы

* Анықталған интегралдың қасиеттері

* Анықталған интегралды қолданып жазық фигураның ауданын табу

* Негізгі интегралдар кестесі

ІІІ. Қорытынды.

ІV. Пайдаланылған әдебиеттер.

Кіріспе

Функцияның туындысы берілсе, осы функцияның өзін қалай табуға болады?
Бұл механикалық тұрғыдан, материалдық нүкте қозғалысының белгілі жылдамдығы
бойынша оның қозғалыс заңын табу екенін білдіреді.

Анықтама. Егер Ғ(х) функциясы ∆ аралығында дифференциалданса және

Ғꞌ(х) = f(x), Vx ∆

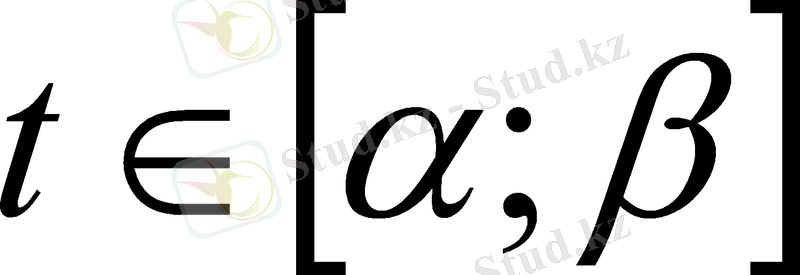Теңдігі орындалса, онда Ғ(х) функциясы f(x) функциясының ∆ аралығындағы
алғашқы функциясы деп аталады.

Мысалы, f(x) = 12√x функциясының ∆ = (0, +∞) аралығындағы
алғашқы функцияларының біреуі –Ғ(х) = √х, өйткені
нүктелері үшін Vx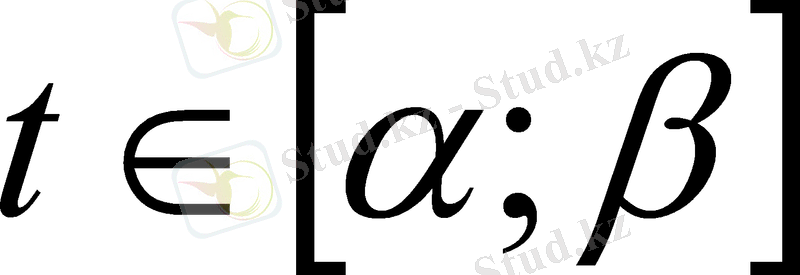(0, +∞) нүктелері үшін (√х)ꞌ = 12√x ;

Негізгі бөлім

Анықталмаған интеграл анықтамасы

f(x) = 2cos2x функциясының ∆ = (-∞, +∞) аралығындағы алғашқы
функцияларының біреуі – F(x) = sin2x, өйткені Vx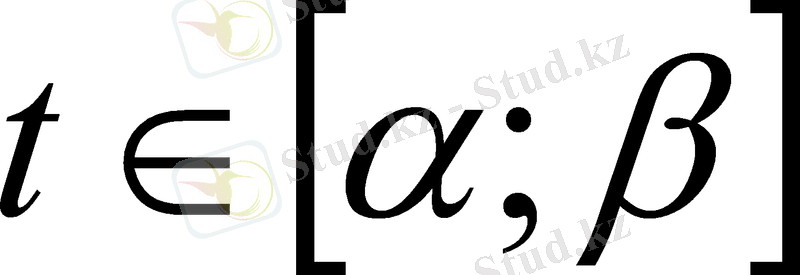(-∞, +∞), (sin2x)ꞌ =
2cos2x.

Егер f(x) функциясының ∆ аралығындағы алғашқы функциясы F(x) болса,
онда кез келген С тұрақты мен F(x) функциясының қосындысы, яғни F(x)+С
функциясы да осы f(x) функциясының ∆ аралығындағы алғашқы функциясы болады,
өйткені Vx 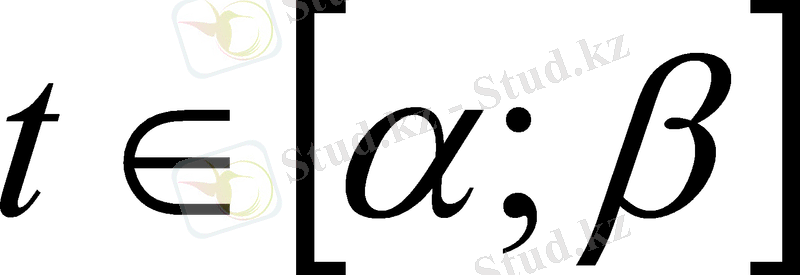∆, (F(x)+С)ꞌ = Ғꞌ(х) +Cꞌ = f(x).

Екінші жағынан, егер f(x) функциясының ∆ аралығындағы алғашқы
функциялары Ғ1(х) пен Ғ2(х) болса: Ғꞌ1(х) = f(x), Ғꞌ2(х) = f(x), Vx ∆,
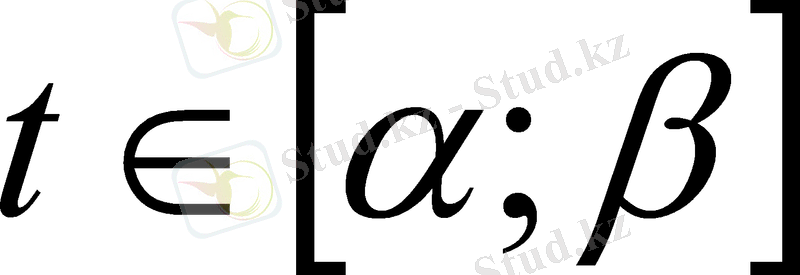онда осы екі алғашқы функциялардың айырымы тұрақты С, яғни Ғ1(х) - Ғ2(х)
=С, Vx 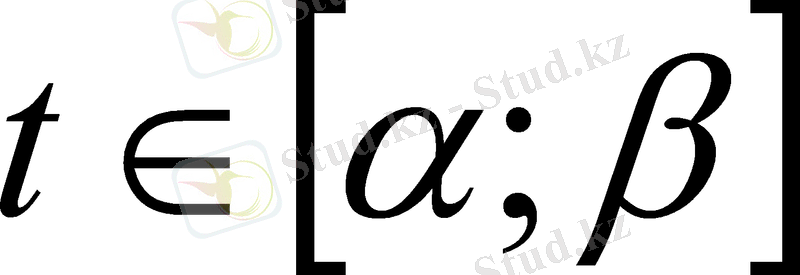∆, болатынын көруге болады. Бұл айтылғандардан, егер f(x)
функциясының ∆ аралығындағы алғашқы функциясы F(x) болса, онда оның осы ∆
аралығындағы кез келген басқа алғашқы функциясы Ф(x) = F(x)+С түрінде
болатыны шығады, мұндағы С осы теңдік дұрыс болатындай етіп таңдап алынатын
тұрақты сан. ∆ - кез келген аралық болсын.

Анықтама. f функциясының ∆ аралығындағы барлық алғашқы
функцияларының жиынтығы f функциясының ∆ аралығындағы анықталмаған
интегралы деп аталады және ол ∫ f(x)dx символымен белгіленеді.Мұндағы ∫ -
интеграл белгісі; f(x) - интеграл астындағы функция; f(x)dx - интеграл
астындағы өрнек.

Егер, f(x) функциясының қандай да бір алғашқы функциясы F(x) болса,
онда келесі теңдікті жазуға болады:

∫ f(x)dx = F(x) + C, C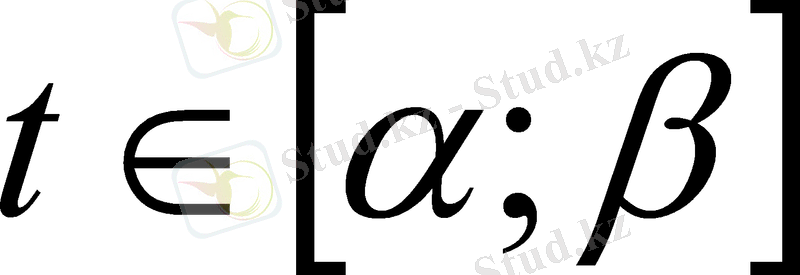R
(1)

Әрине, анықтама бойынша ∫ f(x)dx ={F(x) + C} деп жазылуға тиіс,
бірақ оны (1) түрінде жазу қалыптасқан.

Ескерту. ∫ f(x)dx символы f функциясының алғашқы функцияларының жиыны
болғанымен, есептеу барысында олардың бірімен ғана амалдар орындалады да,
есептеу аяқталған соң, жоғарыда келтірілген пайымдауларға сүйеніп, С
тұрақтысын қосып жазу арқылы алғашқы функциялар жиынына көшеді.

Интеграл астындағы f функциясының dx дифференциалына көбейтіліп
жазылуынан алғашқы функцияның қайсы айнымалы бойынша ізделінетінін көреміз,
мысалы,

∫ x2 zdx = x3z3 + C, ∫ x2 zdz = x2 z22 + C

Оның басқа да ыңғайлы жақтары (интегралда айнымалы ауыстыру және т.б.)
алдымызда көрсетіледі.

f(x) функциясының алғашқы функциясын табу амалын f(x) функциясын
интегралдау амалы деп атайды.

Жоғарыда, егер f(x) үшін ∆ аралығында алғашқы функция бар болса, онда
ол жалғыз емес екенін көрдік. Осыған орай мынадай сұрақ туады: (a,b)
аралығында кез келген f(x) функциясының алғашқы функциясы бар ма?

Кейінірек, егер f(x) функциясы (a,b) аралығында үзіліссіз немесе
монотонды болса, онда f(x) үшін осы аралықта алғашқы функция бар болатынын
көреміз. Қазірше кез келген үзіліссіз функцияның алғашқы функциясы бар деп
қабылдап, үзіліссіз функциялармен жұмыс істейміз.

Анықталмаған интегралдың қасиеттері

Анықталмаған интегралдың қасиеттерін қарастырайық.

Егер f(x) функциясының алғашқы функциясы F(x) болса, онда интеграл
астындағы өрнек

∫ f(x)dx = Fꞌ(x)dx = dF(x)

алғашқы F(x) функциясының дифференциалы. Сондықтан, (1) теңдікті келесі
түрде де жазуға болады.

∫ dF(x) = F(x) + C;

А) A* f(x)dx = A∫ f(x)dx + C, A – тұрақты сан

Б) ∫ [f(x) + g(x)]dx = ∫ f(x)dx + ∫ g(x)dx + C

Соңғы (Б) теңдік интегралдың аддитивтілік қасиеті деп аталады.

Мысалы, (Б) қасиетін көрсетейік.

[Ф1(х)]ꞌ = (∫f(x)dx+ ∫g(x)dx)ꞌ = (∫f(x)dx)ꞌ + (∫g(x)dx)ꞌ= анықтама
бойынша =

= f(x) + g(x);

[Ф2(x)]ꞌ = (∫[f(x)+g(x)]dx)ꞌ = анықтама бойынша = f(x) + g(x).

Сонымен Ф1(х) және Ф2(х) функциялары f(x) + g(x) функциясының екі
алғашқы функциясы болып тұр. Ендеше, олардың айырымы С тұрақты сан:

Ф1(х) - Ф2(х) = ∫[f(x)+g(x)]dx) - (∫f(x)dx + ∫g(x)dx) = C,

Яғни (Б) теңдік орындалады. (А) теңдігі де осылай дәлелденеді.

Егер f(x) функциясының алғашқы функциясы F(x) болса, онда f(ax+b)
функциясының алғашқы функциясы 1а Ғ(ax+b) болады, яғни

∫ f(ax+b)dx = 1а Ғ(ax+b) + C.

Дифференциалдау формуласынан шығатын интегралдар кестесін келтірейік
(теңдіктер бөлшектің бөліміндегі функциялар нөлге тең емес нүктелерде
дұрыс).

* ∫0 dx=C

* ∫ xa dx=xα+1α+1+C, Vα≠-1.

* ∫ x-1 dx=∫ dxx=Inx+C, Vx≠0.

* ∫ ax dx= ax Ina+C, a›0, a≠1. Дербес жағдайы: егер a=e болса, онда
∫exdx=ex+C.

* ∫ sin xdx=cos x+C, ∫ cos xdx=sin x+C.

* ∫ dxcos2 x=tg x+C; ∫ dx sin2 x= ctgx+C.

* ∫ sh xdx=ch x, ∫ ch xdx=sh x+C, (мұнда sh x= ex-e-x2; ch x= ex+e-x2).

* ∫ dxch2x=th x+C; ∫ dxsh2x=cth x+C.

* ∫ dxx2+a2=1a arctg xa+C.

* ∫ dxx2-a2=1aIn x-ax+a+C, x≠a

* ∫ dx √a2-x2= arcsin xa+C, x‹a

* ∫ dx √x2-a=Inx+√x2+a+C, x2+a›0, a≠0.

* ∫ dxsin x=Intg x2+C.

* ∫ dxcos x=Intg (x2+π4)+C.

Бұл теңдіктердің дұрыстығын дифференциалдау арқылы тексеруге болады.
Мысалы, 3) формуланы дәлелдейік.

▼x≠0 үшін, x=x*sign x теңдігінен xꞌ=(x*sign x)ꞌ=sign x аламыз.
Олай болса, (Inx+C)ꞌ=1x*xꞌ= sign xx*sign x=1x, x≠0.▲

Енді 12) формуланы дәлелдейік.

▼(Inx+√x2+a+C)ꞌ=1x+√x2+a*x+√x 2+aꞌ=1x+√x2+a*sign
(x+√x2+a)*(x+√x2+a)ꞌ=1x+√x2+a*si gn (x+√x2+a)*(1*x+√x2+a)= sign (x+√
x2+a)(x+ √x2+a)*x+√x2+a√x2+a=1√x2+a.▲

Элементар функциялардың туындылары элементар функциялар болатыны
белгілі. Ал элементар фунуцияларды интегралдау нәтижесінде элементар
функция алынбауы да мүмкін.

Мысалы, келесі интеграл астындағы фунциялардың элементар функциялар
еместігін дәлелденген:

∫e-x2dx – Пуассон интегралы;

∫cosx2dx, ∫sinx2dx – Френель интегралы;

∫dxlnx – интегралдық логарифм;

∫(cosxx)dx – интегралдық косинус;

∫(sinxx)dx – интегралдық синус;

∫(exx)dx, ∫dx√1+x3 т.с.с.

Бұл интегралдарды есептеу үшін, мысалы, интеграл астындағы функцияны
дәрежелік қатарларға жіктеп, мүшелеп интегралдау әдісін қолданады.

Анықталған интеграл

І – есеп. Х өсіндегі [a,b] кесіндісін – сызықтық біртекті емес
стержень (желі) ретінде қарастырайық. Оның массасының үлестіру тығыздығы
ρ(х) – үзіліссіз функция болсын. Осы стерьженнің массасын анықтау керек.

▼ а) стерьженді кез келген a = x0 ‹ x1 ‹ ... , ‹ xn = b нүктелерімен n
бөлікке бөліктейміз: [a,b] = U [xj,xj+1];

б) Әрбір [xj,xj+1] бөліктен кез келген ξj нүктесін ξj 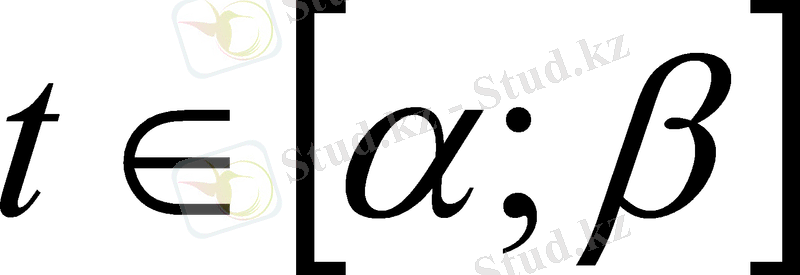[xj,xj+1],
j = 0,1,...,n-1 алып, келесіинтегралдық қосындыны
құраймыз: Mn = Σ ρ( ξj)∆xj. Ал [xj,xj+1] аралығында ρ(х) функциясының
өзгеруі шамалы ғана болғандықтан, стерьженнің[xj,xj+1] кесіндісіне сәйкес
массасының жуық мәні ρ( ξj)* ∆xj = ρ( ξj)( xj+1 - xj) тең болғандықтан, Mn
қосындысы бүкіл стерженнің массасын жуықтайды;

в) Стерженнің массасының дәл мәнін, ұзындығы ең үлкен бөлікше
кесіндіні нөлге ұмтылдыра отырып, Mn интегралдық қосындының шегіне өту
арқылы аламыз:

М = lim Σ ρ( ξj)∆xj, ∆xj = xj+1 - x j
(1)

Осы сияқты, қандай да бір дене f күшінің әсерінен [a,b] аралығында
түзу сызықпен қозғалғандағы А жұмысын анықтауға болады:

А = lim Σ f( ξj)∆xj

Тағы да басқа көптеген физикалық есептерді осы тәсілмен шешуге болады.

Бұл есептер бізді [a,b] кесіндісінде берілген, тегі әртүрлі
функцияларға жасалатын бір ғана математикалық амалға алып келіп отыр. Бұл
амал функцияны кесіндіде интегралдау деп, ал оның нәтижесі функцияның
кесіндідегі анықталған интегралы деп аталады. Енді жалпы жағдайға көшейік,
үзіліссіз және теріс емес функцияға жасалған үш амалды сипаты кез келген
функция үшін қайталайық.

] кесіндісінде у = f(x) функциясы берілсін.

[a,b] кесіндісін кез келген a = x0 ‹ x1 ‹ ... , ‹ xn = b нүктелерімен
[xj,xj+1], i = 0,1,...,n-1, бөліктерге бөлеміз ( оны R бөліктеуі деп
атайық);

Әрбір [xj,xj+1] бөліктен кез келген ξj [xj,xj+1] нүктелерін алып, f
функциясының R бөліктеуіне сәйкес интегралдық қосынды деп аталатын

SR(f) = Σ f( ξj)∆xj, ∆xj = xj+1 - xj
(2)

қосындыны құрамыз;

Max ∆xj → 0 ұмтылдырып, интегралдық қосыныдының шегіне өтеміз.

Егер бұл шек бар болса, онда ол f функциясының [a,b]
кесіндісіндегі Риман бойынша анықталған интегралы деп аталады да,

a∫b f(x)dx = lim Σ f( ξj)∆xj, ∆xj, (a‹b)

түрінде белгіленеді. Мұндағы a мен b сандары – анықталған интегралдың
сәйкес төменгі және жоғарғы шегі деп аталады.

Назар аударыңыз. Анықтамада айтылған, [a,b] кесіндісін бөліктеуді де,
ξ нүктесін таңдап алуды да ақырсыз көп тәсілдермен жасауға болады. Егер f
функциясының интегралдық қосындысының шегі бар болса, онда ол осы
тәсілдерге тәуелсіз ( кез келген R бөліктеу мен ξ нүктелері үшін) бір санға
ғана тең болуы керек. Бұл жағдай, әрине, f функциясының сипатына
байланысты. Мысалы, егер f функциясы [a,b] кесіндісінде үзіліссіз немесе
монотонды болса, онда оның интегралдық қосындысының шегі бар.

Жоғарыдағы анықтаманы үзіліссіз функциялар үшін француз математигі
О.Л.Коши (1789-1857), ал жалпы жағдай үшін неміс математигі Б.Ф.Риман (1826-
1866) енгізген.

(2) шек Риман интегралы, ал f(x) функциясы Риман мағынасында
интегралданатын функция деп аталады. Біз алдымызда, Риман интегралын тек
интеграл деп атайтын боламыз.

(1) – (2) теңдіктерден мынадай қорытынды жасауға болады:

* Ох өсінің [a,b] кесіндісі бойымен орналасқан үлестіру тығыздығы ρ(х)
біртексіз стерженнің М массасы осы ρ(х) функциясының [a,b] кесіндісіндегі
анықталған интегралына тең:

М = a∫b ρ(x)dx

Қандай да бір дене f күшінің әсерінен [a,b] аралығында түзу сызықпен
қозғалғандағы А жұмысы, f функциясының [a,b] кесіндісіндегі анықталған
интегралына тең: А = a∫b f(x)dx.

Анықталған интегралды оның анықтамасы арқылы есептеу оңай жұмыс емес.
Сондықтан анықталған интегралды есептеудің басқа тәсілін табу қажет болды.
Бұл бағытта ағылшын физигі И.Ньютон (1643-1723) және неміс математигі
Г.В.Лейбниц (1646-1716) шешуші жұмыс атқарды. Олар математикалық анализдің
маңызды ұғымдары интеграл мен туындыны байланыстыратын теореманы дәлелдеді.
Оның түйіні ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.