Функцияның модулі

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 18 бет
Таңдаулыға:

Мазмұны
І Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...2
... ... ... ... ... ... ... ... .. ... ... ... .
II Негізгі 4
бөлім ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ... .. .
1.1Синусоидалық токтарды комплекстік жазықтықта 4
кескіндеу ... ... ... ..
1.2Комплекстік жазықтықтағы синусоидалық финкцияларға қосу және алу
амалдарынқолдану ... ... ... ... .. ... ... ... ... ... ... ... ...7
... ... ... ... ... ... ...
1.3Комплекстік сандарға амалдар қолдану 9
1.4Синусоидалық токтың комплекстік мәндері үшінОм және Кирхгорф
заңдары 10
... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ... ..
Есептің 14
қойылымы ... ... ... ... ... ... .. ... ... ... ... ... ... ... ...
... ... ... ... ... ... ...
ІІІҚорытынды ... ... ... ... ... . ... ... ... ... ... ... ... ... ... 17
... ... ... ... ... ... ... ... .. ... ...
Пайданылған 18
әдебиеттер ... ... ... ... ... ... ... ... ... ... ... ... ... ...
... ... ... ... ...

Кіріспе

Қоғамның дамуындағы электр электр энергиясының рөлі мен маңызы елеулі
орын алатындығы көпшiлікке мəлім. Электр энергиясыөмірдің барлық
салаларынында соншалықты кең таратылуының бастысебебінің бірі -
электромагниттік энергияны өте аз шығынмен алысқашықтыққа беру жəне оны
энергияның басқа да түрлеріне:механикалық, жарық, жылу, химиялық жəне т. б.
түрлендіру ыңғайлы.
Электр энергиясы кез-келген қуаты бар қабылдағыштарға оңай тар- алады.
Байланыс техникаларындағы, автоматикадағы жəне есептеу тех-никаларындағы
қолданылатын қондырғылардың пайдаланатынқуатының өлшемдері ваттың
үлестерімен есептелінсе, электрлікқондырғыларда (қозғалтқыштарда, жылытқыш
қондырғыларда) қуаттыңөлшемдері мыңдаған жəне он мыңдаған килловатты
көрсетеді.
„Электротехника жəне электроника негіздері” курсының пəнi дeп, тіз-
бектер мен өpicтepдeгi өтетін электромагниттік процестерді сандықжəне
сапалық жағынан оқып үйренуді айтады. Физика жəне жоғарыматематика
курстарына негізделген бұл курс, осы заманғыэлектротехникалық
құрылымдардың, əр түрлі кең кластарынақолданылатын инженерлік есептеулер
жəне талдау əдістеріне толыболады. Сонымен қатар „Электротехника жəне
электроника негіздері”курсы өндіріске қажетті болашақ мамандардың
электротехникаданғылыми көз-қарастарының қалыптасып жетілуінде аса
маңыздырөл атқарады.
Электр тізбектерін есептеуді eкi əдіспен баяндап жеткізугеболады:
бipiншi əдіс бойынша, есептеу жұмыстары синусоидалықтоқтың электр
тізбектерінің теориясы бойынша баяндалады. Ал екіншібойынша, əуелі есептеу
əдіci резистивтік тізбектер (тұрақты тоқтізбектері) қатысты қарастырылады
да, сонан соң бұл əдістерсинусоидалық тоқ тізбектеріне ауысады. Сонымен
катар қолдануоблысы кең, ауқымды тұрақты тоқ тізбектерінің есептеулерін
жургізудің нəтижесінде, студенттердің бойында оларға қажетті білікдағдылары
қалыптасады.
”Электротехника жəне электроника негіздері” курсын оқыпүйренудің
барысында студенттердің біліктілігін қалыптастыру, яғниолардың негізгі
заңдарын оқып үйренуде, есептеулерде талдау əдістерінқолдануды үйренуі
көзделеді. Тəжірибелік зерттеулерді электртізбектерде жүретін нақты
кұбылыстар мен процестерге қолданудыүйрету арқылы жүзеге асырады. Бұл
жерде, сол көп санды əдістер ментəсілдерден ең қарапайым, негізгі мақсатқа
жеткізетіндерін ғана, инженерлік біліктілікпен дəл таңдай білуі керектігі
көзделген. Демек,студент өзінің мамандығына сай ”Электротехника жəне
электрониканегіздері” курсынан теориялық жəне тəжірибелік біліктіліктерді
ойдағыдай жеткілікті дəрежеде бойына сіңіруі тиіс.Оқу құралының мақсаты
студенттердің мамандығы бойыншаарнайы пəндерді оқып, оны іс жүзінде
ұйымдастыру үшін”Электротехника жəне электроника негіздері” пəні бойынша
өзіндік жұмыстарды жасауға көмек көрсету болып табылады.
Бұл жұмысың тнегізгі мақсаттары - пəнді тек теориялықжағынан оқып
үйренуді ғана емес, сонымен қатар ондаэлектромагниттік құбылыстар мен
электрлік процестердің қолдануаймақтарын тəжірибелік тұрғыдан қарастыру
мəселелері анықталған. Пəнді оқытудағы басты міндеттердің бірі:
студендентердің”Электротехника жəне электроника негіздері” курсын оқып
үйренулері, яғни білім жəне біліктерді терең жəне саналы түрде бойларына
сіңірулері. Білім негіздері мынадай мəселерді қамтиды: есептеулердіңнəт-
ижелерін талдаудың əдістерін игеру.

1.1 Синусоидалық токтарды комплекстік жазықтықта кескіндеу

Синусоидалы (айнымалы) тоқ деп синус заңдылығымен өзгеретінтоқты
айтады: i = Imsinα.
Айнымалы тоқтың тұрақты тоққа қарағанда ерекшелігі, оны алыс қашық-
тықтарға қарапайым айнымалы тоқ генератор құрылғысы менқажетке
пайдаланғанда сенімділігі жоғары қозғалтқыштары бар трансформаторлық
қосалқы станцияларды пайдалана отырып тарата алады.
Электрмагниттік ЭҚК шамасы магнит индукциясынан В, сымныңактивті
ұзындығынан l, өткізгішті қиып өтетін магнит күштіксызықтардың
жылдамдығынан V жəне магнит индукциясының векторымен жылдам-дықтың
векторының бағыттарының арасындағы синусбұрышынан тəуелді болады. Электр
магнитті ЭҚК келесі формуламенанықталады:
e = B ⋅l ⋅V ⋅sin α.
Электр магниттік индукцияның ЭҚК αтəуелділігінқарастырамыз:
α = 0, − е = 0;
α = 90o , − е = max; em= B ⋅l ⋅V ⋅sin 90o = B ⋅l ⋅V = Em;
α =180o , − е = 0;
α = 270o , − е = max; em= B ⋅l ⋅V ⋅sin 270o = −B ⋅l ⋅V = −Em;
α = 360o , − е = 0 .

Em=B* l* V деп белгілейотырып, электр магниттік индукцияныЭҚКанық-тау
формуласы төмендегідей болып анықталады:
e = Emsinα.
Комплекс сандарды кескіндеуге болатын комплекстік жазықтық
бейнеленген.

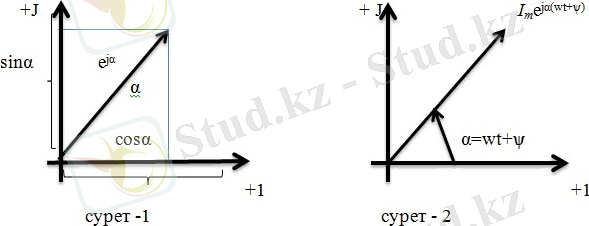
Комплекстік санның нақты және жорамал бөлігі болады.комплекстік
жазықтықтың абсцисса өсі бойына комплекстік санның нақты бөлігін, ал
ординатаға жорамал санның бөлігін салады. Нақты мәндер өсіне +1-ді, ал
жорамал мәндер өсіне +j –ді (+j=-1) саламыз.
Математика курсынан белгілі Эйгер өрнегі бойынша:

ejα=cosα+jsinα. (1)

Комплекс жазықтықтағы ejα - комплекстік саны векторды бейнелейді, ол
бірге тең және заттық мәндер өсімен (+1 өсімен) α бұрыш жазайды. Альфа
бұрышы +1 өсінен сағат тілі бағытына қарсы бағытта саналады. Функцияның
модулі:
Мұндағыejα- функциясының +1 өсіне проекциясы cosα –ға ,ал +jөсіне
проекциясы sinα- ға тең болады. Егер ejα– функциясының орнына Imejα-
ныалсақ онда

Im ejα =Imcosα+jImsinα.

Комплекстік жазықтықта бұл функция, ejα - функциясы сияқты, +1 өсіне α
–бұрышымен бейнеленеді, бірақ вектордың ұзындығы Imесе көп болады.

Imejα(wt+ѱ)=Imcos (wt+ѱ)+jImsin (wt+ѱ). (2)
Мұндағы Imcos (wt+ѱ) қосылғыш I m ejα(wt+ѱ)– дің нақты бөлігін (Re)
құрайды, сондықтан

Imcos (wt+ѱ) = Re I m ejα(wt+ѱ)

ал Imsin (wt+ѱ) функциясы I m ejα(wt+ѱ)өрнегінң жорамал бөлігі
(Im) болып табылады, демек

i =Imsin (wt+ѱ) =ImI m ejα(wt+ѱ). (4)

Сонымен синусоидамен өзгеретін және і- тогын I m ejα(wt+ѱ)түрінде,
немесе діл осы сияқты, бірақ I m ejα(wt+ѱ) айналу векторының +j өсіне
проекциясы түрінде көрсетуге болады.
Комплекстік жазықыұтарда, бірдейлік үшін, уақытқа байланысты
синусоидалық түрде өзгеретін вектордың (wt= 0 болатын уақыт кезендегі)
шамасы қабылданған. Сонда вектор мынадай болады:

I m ejα(wt+ѱ)=I m ejα =I m .

Мұндағы I m - модулі I m - ге тең, комплекстік шама; ѱ бастапқы
фазаға тең, комплекстік жазықтықтың +1 өсіне I m векторын жасайтын бұрыш.
I m - шамасы і – тогының комплекстік
амплитуасы.Комплекстікамплитудакомп лекстік жазықтықта, wt= 0 болған уақыт
кезеніңдегі і- тогын бейнелейді. І –тогының немесе U – кернеудегі үстіне
қойылған нүкте бұл шамалардың уақытқа байланысты синусоида заңымен
өзгеретінін көрсетеді.
Осы айтқанымызға түсініктеме берейік. Айталық, і = 8sin(wt+20)A
болсын. Осы токты комплекстік амплитуда өрнегі түрінде жазайық. Бұл
жағлайда I m = 8 A, ѱ=20΄ A. Демек, I m ej 20΄. Айта.лық,
комплекстік амплитудаI m = 25ej 20΄A болсын дейік. Енді осы токтың лездік
мәні үшін қрнек жазайық. Комплекстік амплитудадан оның лездік мәніне көшу
үшін I m– ді ejwt-е көбейтеміз де, алынған көбейтіндінің жорамал бөлігін
алдындағы коэффициентті аламыз:

i = Im25e-j 30΄ejwt=I m 25ej(wt-30΄)=25sin(wt-30΄).

1.2 Комплекстік жазықтықтағы синусоидалық финкцияларға
қосу және алу амалдарын қолдану.

Жиіліктері бірдей екі токтың ( і2 және і2 ) қосу керек болсын дейік.
Сонда олардың қосындылары сондай жиілікті токты береді:
і = і1 + і2

i1 =I1msin (wt+ѱ) ;i 2=I2msin (wt+ѱ) ;

i =Imsin (wt+ѱ); (1.2.1)

Демек, і- тогының Im - амплитудасы, ѱ – бастапқы фазасын анықтау
қажет. Осыған сәйкес комплекстік жазықтықта -тогын І1m = І1mejѱ1 , ал і2
–тогын І2m = І2mejѱ2 векториар түрінде бейнелейміз.І1m және І2m -
векторларының геометрриялық қосындылары Іm = Іmejѱ қосынды, токтың
комплекстік амплитудасын береді. Токтың Іm - амплитудасы қосынды вектордың
ұзындығы, ал бастапқы ѱ - фазасыосы вектор мен +1 өсінің арасындағы
бұрыш ретінде анықталады .
Екі токтың айырымын анықтау үшін, комплекстік жазықтықта қосу
операциясын емес, қайта, тиісті вектордың айырымын анықтау операциясын
жүргізу керек.

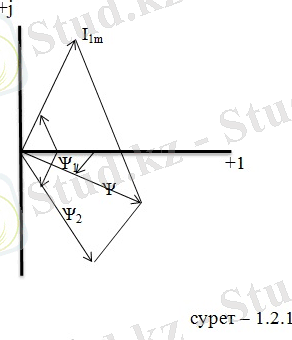
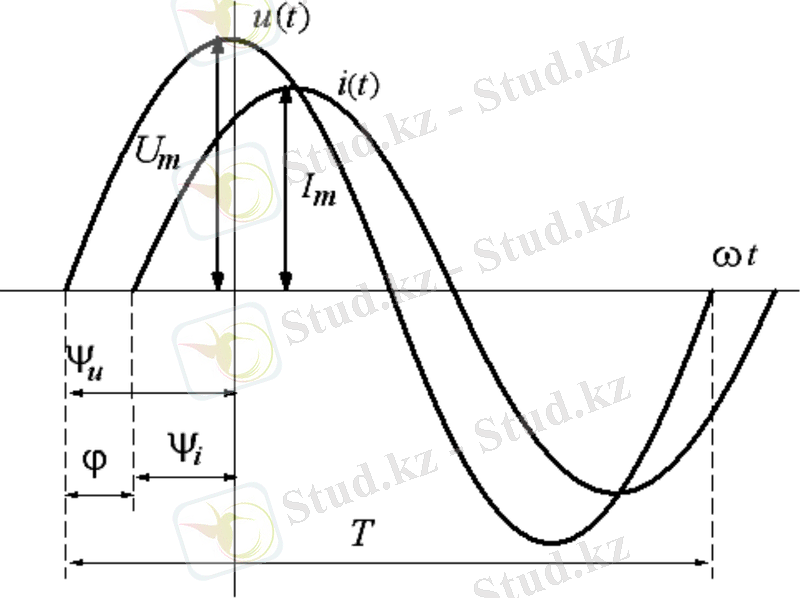
сурет – 1.2.2
Егер І1m , І2m және Іmвекторлары координата бас нүктесінің
айналасында ω – бұрыштық жылдамдықпен айналатын болса, онда векторлардың
бір – бірімен салыстырғандағы еш өзгерусіз қалатынына көңіл аударумыз
қажет.
Векторлық диограмма деп бір уақыт бойынша бірдей жиілікпен синусоида
заңымен өзгеретін, фазаларына байланысты бір – бірімен салыстырғанда, дұрыс
бағытталулары сақтала отырып салынған комплекстік жазықтықтағы
векторлардың жиынтығын айтамыз. Электр тізбегінің бөлігі арқылы
синусоидалық токтар жүргенде ток көзінің энергиясын тұтыну процесі жүріп
жатады. Энергияның келіп тұру жылдамдығы қуатпен сипатталады.

1.3 Комплекстік сандарға амалдар қолдану
Тізбектегі айнымалы токтарды есептеуде комплекстік сандармен әр түрлі
жұмыстарды орындауға тура келеді. Мысалы, тізбектің бөлігіндегі кедергілер
немесе тізбек тұтасымен – бұл бір комплекс , яни ток, кернеу э.қ.к –
комплекстер және тағы басқа Ом заңы бойынша токты табу үшін э.қ.к – і
комплекс кедергі комплексне бөлу керек.
Математикада блетініміздей комплекстік сандарды мынадай түрде жазамды:
алгебралық а+jb, көрсеткіштікcejφжәне тригонометриялық сcosφ+ ic sinφ.
Екі және одан да көп комплекстік сандарды қосу алгебралық түрде жазу
арқылы жүргізіледі. Мұнда олардың нақты бөлігі бір бөлек, жорамал бөлігі
бір бөлек қосындаланады.
( а1 + jb1 ) + (а2 + jb2 ) + ( а3 - jb3 )=
= (a1 + a2 + a3) + j( b1 + b2 - b3 ).
Комплекстік сандарды көбейту және бөлуді дәрежелік трде жазып,
жргізген орынды. Айталық c2ejφ2 – комплексіне бөлу керек болсын дейік.
Сонда бөлуді орындағанда қортындысында коиплекс алынады:

c2ejφ2 =c2ejφ2
Қортынды комплекстік c3 – модулі әлгі c1 мен c2 – нің бөліндісіне б,
аргументік φ3 =φ1 –φ2 айырымына тең болады.
Жоғарыдағы c1 және c2 - комплекстерінің бір – біріне көбейтетін
болсақ, онда қорытқы комплекс
c4ejφ4 =c1ejφ1c2ejφ2 =c1ej( φ1+φ2 ) .

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.