Математическое моделирование волновой динамики изотропной упругой среды при дозвуковых транспортных нагрузках методом обобщённых функций и тензором Грина


Министерство образования и науки Республики Казахстан
Казахский национальный университет им. аль-Фараби
«Допущена к защите»
Заведующий кафедрой Математического
и компьютерного моделирования Исахов А. А.
ДИПЛОМНАЯ РАБОТА
На тему: «МОДЕЛИРОВАНИЕ ДИНАМИКИ УПРУГОЙ СРЕДЫ ПРИ ТРАНСПОРТНЫХ НАГРУЗКАХ»
по специальности
5В070500 - «Математическое и компьютерное моделирование»
Научный руководитель
д. ф. -м. н., профессор
.
РЕФЕРАТ
Тема дипломной работы: «Моделирование динамики упругой среды при транспортных нагрузках».
Ключевые слова : упругая среда, транспортная нагрузка, дозвуковая скорость, уравнения Ламе, тензор Грина, обобщенные решения, метод обобщенных функций.
Цель дипломной работы - моделирование волновой динамики упругой среды при воздействии транспортной нагрузки на основе метода обобщенных функций.
Дипломная работа общим объемом 46 страниц, список использованной литературы состоит из 13 наименований. В работе содержится 26 рисунков.
Работа связана с изучением методов математического моделирования волновой динамики изотропной упругой среды при воздействии на неё транспортной нагрузки и численной реализацией ряда задач. С использованием методов теории обобщенных функции и обобщенного преобразования Фурье, показано, как строятся фундаментальные и обобщенные решения системы транспортных уравнений Ламе, описывающих движение упругой среды при дозвуковых скоростях движения источника возмущений. С использованием тензора Грина - фундаментального решения системы транспортных уравнений Ламе, построены формулы для перемещений в среде при дозвуковых транспортных нагрузках. Проведена компьютерная реализация тензора Грина в системе MathCad-14 для упругих сред, моделирующих грунты, песчаник. Рассмотрена транспортная краевая задача для упругого полупространства, по границе которого движется транспортная дозвуковая нагрузка. Представлено решение этой задачи, построенное на основе метода обобщенных функций. Описана процедура построения решения на основе этого метода. Разработаны программы в системе MathCad-14 для расчета тензоров фундаментальных перемещении, который является одним из ядром интегрального представления решения краевой задачи.
Расчеты, которые были проведены, представлены в виде графиков перемещений массива в окрестности транспортной нагрузки для разных скоростей нагрузки и параметров упругих сред.
РЕФЕРАТ
Дипломдық жұмыстың тақырыбы: « Көлік жүктемелерінде серпімді ортаның динамикасын модельдеу».
Кілттік сөздер: серпімді орта, көлік жүктемелері, субсоникалық жылдамдық, Ламе теңдеуі, Грин тензоры, жалпыланған шешімдер, жалпыланған функциялар әдісі.
Дипломдық жұмыстың мақсаты - жалпыланған функциялар әдісі негізінде серпімді ортаға транспорттық жүк әсер еткен кезде толқындық динамиканы модельдеу.
Дипломдық жұмыстың көлемі 46 бет, қолданылған әдебиет 13 тізімнен құралған. Дипломдық жұмыста 26 сурет бар.
Дипломдық жұмыс изотропты серпімді ортаға транспорттық жүк әсер еткен кездегі толқындық динамиканы математикалық модельдеу әдістерін меңгеріп, ол үшін бірнеше қатар есеп үшін есептеуіш әдісті жүзеге асырумен байланысты. Жалпыланған функциялар теориясының әдістерін және жалпыланған Фурье түрлендірулерін қолдана отырып, серпімді ортаның кернеу көзінің жылдамдығы субсоникалық болған кездегі қозғалысты сипаттайтын теңдеу, яғни Ламе теңдеу жүйелерінің іргелі және жалпыланған шешімін құру көрсетілген. Грин тензорын қолдана отырып, субсоникалық транспорттық жүктеме кезіндегі жылжулар үшін формулалар алынды. Грин тензоры үшін MathCad-14 жүйесінде қара жер және құмтас серпімді орталары үшін есептеуіш әдіс жүзеге асырылды. Межесінде субсоникалық транспорттық жүктеме жүрген кезде серпімді жартыкеңістік үшін шектік есептер қарастырылды. Жлапыланған функциялар әдістерінде негізделген осы есептің шешімі көрсетілген. Осы әдіс негізінде шешімді құру тәртібі сипатталған. MathCad-14 жүйесінде шектік есепті шешудің интегралдық көрсетілімінің бір негізі болып табылатын іргелі жылжулар тензорын есептейтін бағдарлама құрылған.
Өткізілген есептеулер әр түрлі жүктеме жылдамдығы мен серпімді орта параметрлері үшін көлік жүктемесі әсер еткен төңіректегі массив жылжуларының графиктері ретінде көрсетілген.
ABSTRACT
Theme of Diploma: « Modeling of the elastic medium dynamics at transport loads».
Keywords: elastic medium, transport load, subsonic velocity, Lame equations, Green's tensor, generalized solutions, method of generalized functions.
The purpose of the thesis is to simulate the wave dynamics of an elastic medium under the influence of a transport load on the basis of the method of generalized functions.
Thesis work with a total volume of 46 pages, the list of used literature consists of 13 titles. The work contains 26 drawings.
The work is related to the study of methods for mathematical modeling of wave dynamics of an isotropic elastic medium under the influence of a transport load on it and the numerical realization of a number of problems. Using the methods of the theory of generalized functions and the generalized Fourier transform, it is shown how fundamental and generalized solutions of the Lame transport equations system are constructed that describe the motion of an elastic medium at subsonic speeds of the perturbation source. Using the Green tensor, the fundamental solution of the Lame transport equation system, formulas are constructed for displacements in a medium under subsonic transport loads. Computer implementation of the Green tensor in the MathCad-14 system for elastic media simulating soils and sandstone was carried out. The transport boundary value problem for an elastic half-space is considered, along the boundary of which the transport subsonic load moves. A solution of this problem, constructed on the basis of the method of generalized functions, is presented. The procedure for constructing a solution based on this method is described. Programs have been developed in the MathCad-14 system for calculating the fundamental displacement tensors, which is one of the core of the integral representation of the solution of the boundary value problem.
The calculations are presented in the form of graphs of displacements of the array in the vicinity of the transport load for different load velocities and parameters of elastic media.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ6
- ФУНДАМЕНТАЛЬНЫЕ И ОБОБЩЕННЫЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ УПРУГОЙ СРЕДЫ ПРИ ТРАНСПОРТНЫХ НАГРУЗКАХ9
Определяющие параметры и основные уравнения динамики изотропной упругой среды9
- Транспортные решения волнового уравнения. Числа Маха13
- Транспортные решения уравнений Ламе 16
Фундаментальные и обобщённые решения транспортных уравнений Ламе. Тензор Грина 18
Построение тензора Грина при дозвуковых скоростях на основе обобщенного преобразования Фурье 19
Динамика упругой среды при действии сосредоточенных на оси дозвуковых транспортных нагрузок25
- МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИНАМИКИ УПРУГОГО ПОЛУПРОСТРАНСТВА ПРИ ДОЗВУКОВЫХ ТРАНСПОРТНЫХ НАГРУЗКАХ36
2. 1 Постановка задачи в пространстве обобщенных функций36
2. 2 Решение задачи в пространстве обобщенных функций37
2. 3 Постановка дозвуковой транспортной задачи 39
2. 4 Решение краевой задачи и разрешающие сингулярные граничные интегральные уравнения40
2. 5 Компьютерная реализация решения краевой задачи 41
ЗАКЛЮЧЕНИЕ44
СПИСОК ЛИТЕРАТУРЫ45
ВВЕДЕНИЕОбеспечение прочности и надежности сооружений и конструкций, подверженных разнообразным статическим и динамическим нагрузкам, является актуальной научно-технической задачей. Для этого необходимым является изучение их напряженно-деформированного состояния под воздействием внешних сил. Наиболее распространённым среди динамических нагрузок являются движущиеся транспортные нагрузки. При движении транспорта на поверхности земли, в тоннелях или при транспортировке грузов в трубопроводах возникают колебания и волны, нежелательные для их эксплуатации. Для изучения напряженно-деформированного состояния сред и конструкций наиболее эффективными являются методы математического моделирования, которые позволяют изучать реальные физические процессы в средах и конструкциях на их математических моделях с целью прогнозирования их поведения при разнообразных внешних воздействиях.
В данной работе рассматриваются вопросы динамики упругой среды при действии транспортных нагрузок, скорость движения которых меньше скорости распространения упругих волн в среде. Такие нагрузки называются дозвуковыми . Они характерны для современных транспортных средств, скорость движения которых много меньше скорости распространения упругих волн. В настоящее время, в связи с интенсивным развитием высоскоростного транспорта, транспортные задачи становятся очень актуальными и эта актуальность с каждым днём растёт.
Еще в середине прошлого века американские ученые Дж. Д. Коул, Дж. Хаз изучали перемещения и напряжения в линейной упругой среде при действии нагрузки, движущейся с постоянной скоростью в упругой полуплоскости [1] . В своей работе они рассмотрели три случая при плоской деформации: дозвуковой, когда нагрузка движется медленнее, чем скорость распространение сдвиговой волны упругой среды; трансзвуковой, когда скорость нагрузки находится между скоростями распространения сдвиговой и объемной волны; сверхзвуковой случай, скорость нагрузки больше чем скорость распространение объемной волны.
В работе «Напряжения и перемещения в слоистом полупространстве для движущейся линейной нагрузки» учёные
Ф. Баррос, Дж. Луко исследовали динамические перемещения и напряжения в многослойном вязкоупругом полупространстве, создаваемые поверхностной нагрузкой, движущейся с постоянной скоростью, параллельной поверхности полупространства [2] .
В 2001 году учёный из Нидерландов Адрианус де Хуп в своей работе «Проблема движущейся нагрузки в динамике почвы - приближение вертикального перемещения» изучал проблему переноса движущейся точки приложения нагрузки [3] . В работе он использовал модифицированный метод Гагниарда для решения переходных процессов волновых уравнений с использованием вертикальной составляющей перемещении частиц. Он рассмотрел дозвуковой и сверхзвуковой случай в своей статье.
В одном из американских научных журналах в 2010 году вышла статья, где учёные О. Шупин, А. Чабот, Ж. Пио, Д. Дюамель опубликовали работу под названием «Влияние скользящих интерфейсов на отклик слоистой вязкоупругой среды под движущейся нагрузкой». В этой статье был представлен метод вычисления реакции
вязкоупругого слоистого полупространства на движущуюся нагрузку при наличии прослойки [4] . Решение получили с помощью преобразования Фурье. Было показано, что низкие скорости и промежуточный слой скольжения более разрушительны для структуры, когда рассматривается критерий деформации или напряжения.
Как видно из библиографии разработка математических моделей волновых процессов в средах при действии транспортных нагрузок с целью описания реальных физических процессов является целью исследовании многих ученых. Тем не менее не достаточно разработано методов для расчета воздействия транспортных нагрузок, это связано с определенными математическими трудностями в решении этих задач
Математическое моделирование разнообразных процессов, связанных с передвижением транспорта в различных средах, либо перемещением транспортируемых грузов в тоннелях и трубопроводах различного назначения приводит к решению краевых задач механики сплошных сред в классе "бегущих" функций, параметрических и автомодельных по ряду переменных.
Параметр задачи - скорость движения источника возмущений в среде - существенно влияет на тип уравнений движения, который зависит от скоростей распространения волн в средах, так называемых звуковых скоростей. Их может быть несколько в зависимости от вида волн. Тип дифференциальных уравнений, описывающих движение среды, меняется в зависимости от отношения скорости источника возмущений к звуковым скоростям (чисел Маха) . Поэтому приходится строить решения систем уравнений эллиптического, гиперболического или смешанного типов. Для физических задач типичными являются ударные воздействия, сосредоточенные на поверхностях и в точках силы и т. п., которые не описываются гладкими функциями.
Целью работы является изучение волновой динамики изотропной упругой среды при воздействии на неё транспортной нагрузки и построение численной реализации.
В первой главе описываются основные характеристики, описывающие напряженно-деформированное состояние упругой среды среды. С использованием методов теории обобщенных функции и обобщенного преобразования Фурье, показано, как строятся фундаментальные и обобщенные решения системы транспортных уравнений Ламе, описывающих движение упругой среды при дозвуковых скоростях движения источника возмущений, когда скорость движения меньше скорости распространения дилатационных и сдвиговых волн в упругой среде. С использованием тензора Грина - фундаментального решения системы транспортных уравнений Ламе, построены формулы для перемещений и напряжении в среде при дозвуковых транспортных нагрузках. Проведена компьютерная реализация тензора Грина в системе MathCad-14 для упругих сред, моделирующих грунты, песчаники и гранит.
Во второй главе рассмотрена транспортная краевая задача для упругого полупространства, по границе которого движется транспортная дозвуковая нагрузка. Представлено решение этой задачи, построенное на основе метода обобщенных функций. Описана процедура построения решения на основе этого метода.
Новизной дипломной работы является создание программы в системе MathCad-14 для расчета тензоров фундаментальных перемещении и напряжений, которые являются ядрами интегрального представления решения этой краевой задачи.
Проведенные расчеты представлены в виде графиков перемещений массива в окрестности транспортной нагрузки для разных скоростей нагрузки и параметров упругих сред.
1 ФУНДАМЕНТАЛЬНЫЕ И ОБОБЩЕННЫЕ РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ УПРУГОЙ СРЕДЫ
ПРИ ТРАНСПОРТНЫХ НАГРУЗКАХ
- Определяющие параметры и основные уравнения
динамики изотропной упругой среды
Пусть
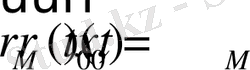 - радиус - вектор материальной точки,
- радиус - вектор материальной точки,
где
x
M
-
Лагранжева координата
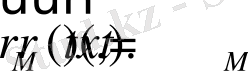
При деформации декартовая сетка преобразуется в криволинейную сетку, как показано в рисунке 1. 1.
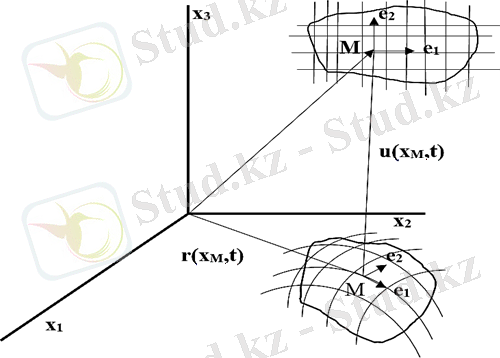
Рисунок 1. 1. Деформация радиус-вектора материальной точки
Для описания движения среды вводится вектор - перемещения

При этом координатные реперы (е
1
, е
2
, е
3
) в декартовой системе координат переходит в
 афинные реперы. Деформация среды описывается
тензором деформации
афинные реперы. Деформация среды описывается
тензором деформации
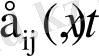
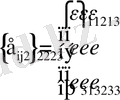
диагональные элементы которого
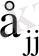 - относительное удлинение - показывают, как удлиняются координатные волокна.
- относительное удлинение - показывают, как удлиняются координатные волокна.
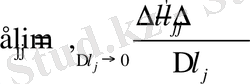
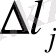 - элементарная длина отрезка вдоль координатной линии.
- элементарная длина отрезка вдоль координатной линии.
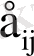 при
при
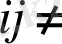 описывают изменение координатных углов
описывают изменение координатных углов
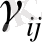 .
.
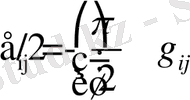 (1. 1)
(1. 1)
Напряжение
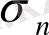 - сила, действующая на единичную площадку
- сила, действующая на единичную площадку
с нормалью
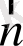
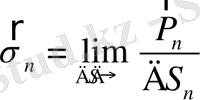
определяется с помощью тензора напряжений
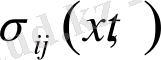
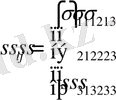
формулой
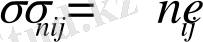 (1. 2)
(1. 2)
Размерность напряжений
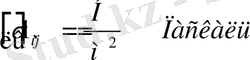
Диагональные компоненты тензора напряжений дают нормальные составляющие напряжений на координатных площадках, перпендикулярных осям с одноименным индексом. Недиагональные компоненты
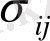 описывают касательные составляющие напряжений, приложенных к координатным площадкам c нормалью X
i
, в направлении оси X
j
.
описывают касательные составляющие напряжений, приложенных к координатным площадкам c нормалью X
i
, в направлении оси X
j
.
При малых деформациях связь между тензорами напряжений и тензорами деформации линейная и описывается законом Гука :
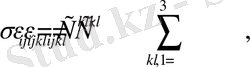 (1. 3)
(1. 3)
где
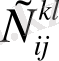 - тензор упругих констант.
- тензор упругих констант.
Среда, свойства которой, отличны в разных направлениях называется анизотропной . Если упругие свойства не зависят от направления, то среда называется изотропной .
Закон Гука для изотропной среды можно представить в следующем виде:
 (1. 4)
(1. 4)
где
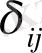 - символ Кронекера,
- символ Кронекера,
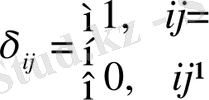
При малой деформации [5]
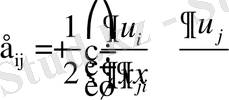 (1. 5)
(1. 5)
Если подставить выражения из системы в закон Гука, то получится:
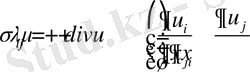 (1. 6)
(1. 6)
где
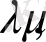 -
упругие параметры Ламе.
-
упругие параметры Ламе.
Уравнение движения твёрдого тела (сплошной среды)
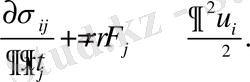 (1. 7)
(1. 7)
где
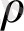 - плотность среды,
- плотность среды,
 -
обьемная сила, действующая на
-
обьемная сила, действующая на
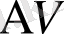 -
элементарный обьем среды.
-
элементарный обьем среды.
Если подставить уравнение (1. 6) в (1. 7), то получится уравнение Ламе
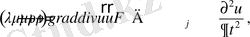 (1. 8)
(1. 8)
Разделив на
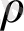 (1. 8) получится
(1. 8) получится
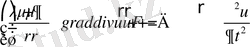
Поскольку в изотропной упругой среде
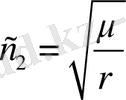 - скорость распространения сдвиговых волн, а
- скорость распространения сдвиговых волн, а
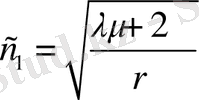 - скорость распространения дилатационных волн (сжатие-расширение), то (1. 8) удобно записать в виде
- скорость распространения дилатационных волн (сжатие-расширение), то (1. 8) удобно записать в виде
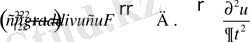 (1. 9)
(1. 9)
Или так
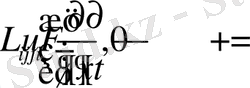 ,
,
где
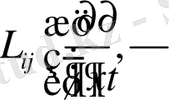 - оператор Ламе имеет вид
- оператор Ламе имеет вид
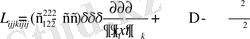 (1. 10)
(1. 10)
Используются эти уравнения для построения транспортных решений. Для этого вначале рассмотрим транспортные решения волнового уравнения.
- Транспортные решения волнового уравнения.
Число Маха
Рассмотрим волновое уравнение
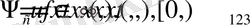 (1. 11)
(1. 11)
где
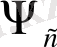 - волновой оператор:
- волновой оператор:
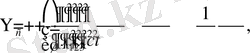
с - скорость распространения волн.
Пусть источник движется вдоль оси X 3 c постоянной скоростью, т. е.
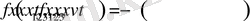
где
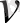 - скорость движения источника.
- скорость движения источника.
Решение (1. 11) ищется в аналогичном виде, т. е. ищется
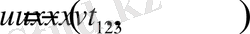 (1. 12)
(1. 12)
Такие решения называются транспортными.
Если обозначить величину
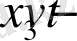 , как z, для дальнейшего перехода в подвижную систему координат
, как z, для дальнейшего перехода в подвижную систему координат
 .
.
Подставив (1. 12) в (1. 11) получится
 (1. 13)
(1. 13)
(1. 13) - это волновое уравнение в подвижной системе координат. Здесь возникает безразмерная величина
М
, которую называют
числом Маха:
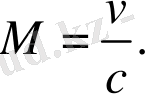
Легко видеть, что (1. 13) приобретет следующий вид
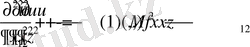
Если ввести обозначение
 , то в зависимости от значения числа Маха будет меняться тип уравнения.
, то в зависимости от значения числа Маха будет меняться тип уравнения.
При дозвуковых скоростях
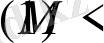 уравнение будет эллиптического типа
уравнение будет эллиптического типа
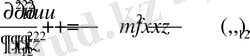 (1. 14)
(1. 14)
При сверхзвуковых скоростях
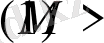 уравнение будет строго гиперболического типа
уравнение будет строго гиперболического типа
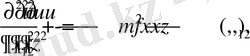 (1. 15)
(1. 15)
При звуковой скорости
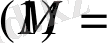 уравнение будет параболического типа
уравнение будет параболического типа
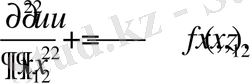 (1. 16)
(1. 16)
Для того, чтобы построить решение уравнении (1. 12) - (1. 14), необходимо взять свертку фундаментального решения с правой частью уравнения.
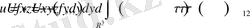 (1. 17)
(1. 17)
Дозвуковой случай. Уравнение (1. 14) напоминает нам уравнение Лапласа. Необходимо сделать замену переменных в (1. 14) для того, чтобы получить уравнение Лапласа.
Если сделать следующую замену
 , то получится
, то получится
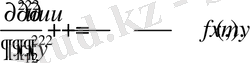 (1. 18)
(1. 18)
Фундаментальное решение для уравнения Лапласа, затухающее на бесконечности, известно из теории уравнении математической физики
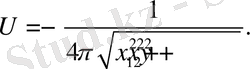 (1. 19)
(1. 19)
Условия затухания на бесконечности:

Подставив (1. 19) в (1. 18) получится решения для уравнения (1. 14) в виде свертки:
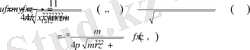 (1. 20)
(1. 20)
где
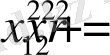 - расстояние до оси Z.
- расстояние до оси Z.
Решение уравнения для источников, описываемых регулярными функциями имеет интегральное представление:
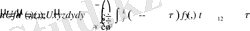 (1. 21)
(1. 21)
Для сосредоточенных источников, описываемыми сингулярными обобщенными функциями, следует использовать определение свертки обобщенных функций [6] . В частности, для источников, движущихся по цилиндрическим поверхностям можно использовать представление
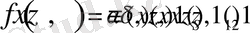
где
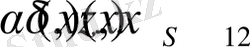 - простой слой на поперечном сечении
S
цилиндрической поверхности. Тогда решение будет иметь вид поверхностного интеграла:
- простой слой на поперечном сечении
S
цилиндрической поверхности. Тогда решение будет иметь вид поверхностного интеграла:
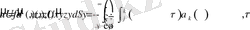 (1. 22)
(1. 22)
Решение представляется в виде суперпозиции фундаментальных решений, распределенных на носителе функции f(x) , интенсивность которых определяется ее значением.
1. 3 Транспортные решения уравнений Ламе
Рассмотрим транспортные решения уравнений Ламе (1. 9)
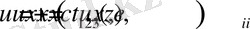
которым соответствуют массовые силы вида
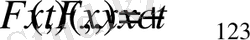 , (1. 23)
, (1. 23)
где нагрузка, движется в противоположном направлении оси х 3 со скоростью с .
Необходимо перейти в подвижную систему координат. Также если обозначить величину
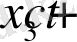 как z, и в результате в новых переменных уравнения движения будет иметь следующий вид
как z, и в результате в новых переменных уравнения движения будет иметь следующий вид
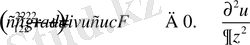 (1. 24)
(1. 24)
Определение. Скорость c называется дозвуковой, если c < c 2 ; межзвуковой (трансзвуковой) , если c 2 <c< c 1 и сверхзвуковой, если c > c 1 . Скорость называется первой или второй звуковой, если c = c j ,
j = 1, 2 соответственно. Также вводятся числа Маха. Здесь их два:
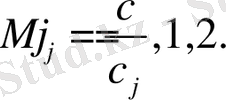
Поделив (1. 24) на с 2 получится следующее уравнение, которое называется транспортное уравнение Ламе.
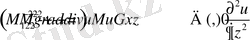
которое эквивалентно
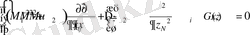 (1. 25)
(1. 25)
где
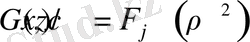
При
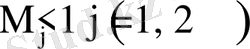 нагрузка дозвуковая, система уравнений эллиптического типа; если нагрузка сверхзвуковая,
нагрузка дозвуковая, система уравнений эллиптического типа; если нагрузка сверхзвуковая,
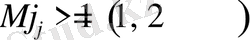 система становится гиперболической; если скорость межзвуковая (трансзвуковая), M
1
<1, M
2
>1 и тип уравнений гиперболо-эллиптический. При звуковых скоростях уравнения параболо-эллиптические, если M
2
=1, а при M
1
= 1 становятся параболо-гиперболическими [7] .
система становится гиперболической; если скорость межзвуковая (трансзвуковая), M
1
<1, M
2
>1 и тип уравнений гиперболо-эллиптический. При звуковых скоростях уравнения параболо-эллиптические, если M
2
=1, а при M
1
= 1 становятся параболо-гиперболическими [7] .
- Фундаментальные и обобщённые решения транспортных уравнений Ламе. Тензор Грина
Для построения решений уравнений Ламе при произволных массовых силах используются фундаментальные решения, которые описывают динамику среды при действии сосредоточенных источников различного типа.
Обозначим
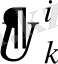 - матрицу фундаментальных решений уравнения движения (1. 25), которая удовлетворяет транспортным уравнениям Ламе
- матрицу фундаментальных решений уравнения движения (1. 25), которая удовлетворяет транспортным уравнениям Ламе
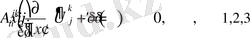 (1. 26)
(1. 26)
где
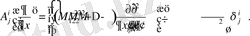
при движении сосредоточенной на оси X 3 силы
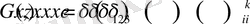 (1. 27)
(1. 27)
Матрица фундаментальных решений определяется неоднозначно, с точностью до решения однородной системы уравнений. Рассмотрим здесь дозвуковой случай: c<c 2 .
ОПРЕДЕЛЕНИЕ. Матрица фундаментальных решений, которая удовлетворяет условиям затухания на бесконечности:

называется тензором Грина уравнений (1. 25) .
При фиксированном k ей соответствует сосредоточенная сила, действующая в направлении координатной оси X k , и бегущая со скоростью c вдоль оси X 3 .
Для произвольной регулярной силы соответствующее решение имеет вид интегрально-тензорной свертки
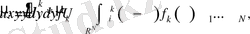 (1. 28)
(1. 28)
- Информатика
- Банковское дело
- Оценка бизнеса
- Бухгалтерское дело
- Валеология
- География
- Геология, Геофизика, Геодезия
- Религия
- Общая история
- Журналистика
- Таможенное дело
- История Казахстана
- Финансы
- Законодательство и Право, Криминалистика
- Маркетинг
- Культурология
- Медицина
- Менеджмент
- Нефть, Газ
- Искуство, музыка
- Педагогика
- Психология
- Страхование
- Налоги
- Политология
- Сертификация, стандартизация
- Социология, Демография
- Статистика
- Туризм
- Физика
- Философия
- Химия
- Делопроизводсто
- Экология, Охрана природы, Природопользование
- Экономика
- Литература
- Биология
- Мясо, молочно, вино-водочные продукты
- Земельный кадастр, Недвижимость
- Математика, Геометрия
- Государственное управление
- Архивное дело
- Полиграфия
- Горное дело
- Языковедение, Филология
- Исторические личности
- Автоматизация, Техника
- Экономическая география
- Международные отношения
- ОБЖ (Основы безопасности жизнедеятельности), Защита труда


