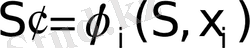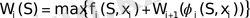Задача распределения ресурсов на расширение производства методом динамического программирования


МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ
РЕСПУБЛИКИ КАЗАХСТАН
Казахский национальный технический университет
им. К. И. Сатпаева
Кафедра технической кибернетики
Пояснительная записка
к курсовому проекту
по дисциплине «ТОКС»
На тему: Задача распределения ресурсов на расширение производства
СОДЕРЖАНИЕ
Задание . . . . 3
Введение . . 4
- Краткая теоретическая часть…. . . . . 5
- Основная часть. . ………. . 8
2. 1. Словесная формулировка задачи . . . . . . 8
2. 2. Математическая постановка задачи. . …9
2. 3. Алгоритм10
2. 4. Решение. . 11
Заключение. 16
Список литературы . . 17
Приложение . . . . . . . 18
1. Программный продукт. . . . . 19
2. Листинг программы
+
Задание
Задача распределения ресурсов на расширение производства
ВАРИАНТ 5
Пусть в группе из n дочерних предприятий фирмы выделены дополнительные средства на расширение производства. По каждому дочернему предприятию известен возможный прирост g i (x) для i=1, …, n выпуска продукции в зависимости от выделенной ему суммы x.
Требуется распределить средства C между дочерними предприятиями так, чтобы общий прирост фирмы ϕ n (C) выпуска продукции был максимальным.
Исходные данные приведены в таблицах 1, 2.
Примечания:
- Для решения задачи следует использовать метод динамического программирования. Общий вид функционального уравнения Беллмана можно взять для данной задачи в следующем виде:
ϕ n (x) = max [g n (x) + ϕ n-1 (C-x) ] .
0≤x≤C
- Для упрощения расчётов значенияxпринимать кратным 20 тыс. у. е.
- Просчитать по шагам вручную, сведя в таблицу результаты. В пояснительную записку включать полностью просчет по шагам. Дать подробную интерпретацию полученных результатов.
- Провести моделирование на PC и сравнить с расчётными данными.
Введение
В наше время, наука уделяет все большее внимание вопросам организации и управления, это обусловлено целым рядом причин. Быстрое развитие и усложнение техники; увеличение масштабов и стоимостей проводимых мероприятий; широкое внедрение автоматизации в сферу управления - все это приводит к необходимости научного анализа сложных целенаправленных процессов под углом зрения их структуры и организации. От науки требуются рекомендации по наилучшему (оптимальному) управлению такими процессами. Эти потребности практики вызвали к жизни специальные научные методы, которые принято объединять под названием «Исследование операций». Под этим подразумевается применение математических, количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности.
Наиболее сложно обстоит дело с принятием решений, когда речь идет о мероприятиях, опыта, в проведении которых еще не существует и, следовательно, здравому смыслу не на что опереться, а интуиция может обмануть. При планировании приходится опираться на большое количество данных, относящихся не столько к прошлому опыту, сколько к предвидимому будущему. Выбранное решение должно по возможности гарантировать нас от ошибок, связанных с неточным прогнозированием, и быть достаточно эффективным для широкого круга условий. Для обоснования такого решения приводится в действие сложная система математических расчетов.
Для решения практических задач исследование операций располагает целым арсеналом математических средств. К ним относятся: теория вероятностей с ее новейшими разделами (теория случайных процессов, теоретические основы компьютерных систем, теория массового обслуживания) ; математические методы оптимизации, начиная от простейших способов нахождения экстремумов (максимумов и минимумов) и кончая современными методами, такие, как линейное программирование, динамическое программирование и многие другие.
В этой курсовой работе используется метод динамического программирования.
1. Краткая теоретическая часть
Динамическое программирование (иначе, «динамическое планирование») представляет собой особый математический метод оптимизации решений, специально приспособленный к многошаговым (или многоэтапным) операциям.
Многошаговую задачу можно решать по-разному: либо искать сразу все элементы решения на всех m шагах, либо же строить оптимальное управление шаг за шагом, на каждом этапе расчета оптимизируя только один шаг. Обычно второй способ оптимизации оказывается проще, чем первый, особенно при большом числе шагов.
Такая идея постепенной, пошаговой оптимизации и лежит в основе динамического программирования. [1]
С первого взгляда эта идея может показаться довольно тривиальной. В самом деле, чего, казалось бы, проще: если трудно оптимизировать операцию в целом, то разбить ее на ряд шагов; каждый такой шаг будет отдельной, маленькой операцией, оптимизировать которую уже нетрудно. Надо выбрать на каждом шаге такое управление, при котором эффективность этого шага максимальна.
Принцип динамического программирования отнюдь не предполагает, что каждый шаг оптимизируется отдельно, независимо от других; что, выбирая шаговое управление, можно забыть обо всех других шагах. Напротив, шаговое управление должно выбираться с учетом всех его последствий в будущем. Планирование должно быть дальновидным, с учетом перспективы. Что толку, если мы выберем на данном шаге управление, при котором эффективность этого шага максимальна, если в дальнейшем это помешает нам получить хорошие результаты других шагов?
Пусть, например, планируется работа группы промышленных предприятий, из которых часть занята выпуском предметов потребления, а остальные производят для них машины. Задача операций - получить за m лет максимальный объем выпуска предметов потребления.
предметов потребления. Допустим, планируются капиталовложения на первый год. Исходя из узких интересов данного шага, мы должны были бы все средства вложить в производство предметов потребления, пустить имеющиеся машины на полную мощность и добиться к концу года максимального объема продукции. Имея в виду будущее, необходимо выделить какую-то долю средств и на производство машин. При этом объем продукции за первый год, естественно, снизится, зато будут созданы условия, позволяющие увеличивать ее производство в последующие годы. [4]
Значит, планируя многошаговую операцию, необходимо выбирать управление на каждом шаге с учетом его будущих последствий на еще предстоящих шагах. [2]
Поэтому процесс динамического программирования разворачивается от конца к началу: раньше всех планируется последний, m -й шаг. А как его спланировать, если мы не знаем, чем кончился предпоследний? Очевидно, нужно сделать разные предположения о том, чем кончился предпоследний (m-1) -й шаг, и для каждого из них найти такое управление, при котором выигрыш (доход) на последнем шаге был бы максимален. Решив эту задачу, мы найдем условное оптимальное управление на m -м шаге, т. е. то управление, которое надо применить, если (m-1) -й шаг закончился определенным образом. [1]
Таким образом, в процессе оптимизации управления методом динамического программирования многошаговый процесс «проходится» дважды: первый раз - от конца к началу, в результате чего находятся условные оптимальные управления и условные оптимальные выигрыши.
Второй раз от начало к концу, когда нам остается только «прочитать»
Уже готовые рекомендации и найти безусловное оптимальное управление,
состоящее из оптимальных шаговых управлений.
Одним словом, на каждом шагу ищется такое управление, которое обеспечивает оптимальное продолжение процесса относительно достигнутого в данный момент состояния. Этот принцип выбора управления называется принципом оптимальности. Само управление, обеспечивающее оптимальное продолжение процесса относительно заданного состояния, называется условным оптимальным управлением на данном шаге. [7]
Теперь предположим, что условное оптимальное управление на каждом шаге нам известно: мы знаем, что делать дальше, в каком бы состоянии ни был процесс к началу каждого шага. Тогда мы можем найти уже не «условное», а просто оптимальное управление на каждом шаге. [3]
Первый вопрос на который нужно ответить ставящему задачу: какими параметрами характеризуется состояние управляемой системы S перед каждым шагом? От удачного выбора этих параметров часто зависит возможность успешно решить задачу оптимизации.
Как быт с числом шагов m? С первого взгляда может показаться, что чем больше m, тем лучше. Это не совсем так. При увеличении m возрастает объем расчетов, а это не всегда оправдано. Число шагов нужно выбирать с учетом двух обстоятельств:
- шаг должен быть достаточно мелким для того, чтобы процедура оптимизации шагового управления была достаточно мелким для того, чтобы процедура оптимизации шагового управления была достаточно проста.
- Шаг должен быть не слишком мелким, чтобы не производить ненужных расчетов, только усложняющих процедуру поиска оптимального решения, но не приводящих к существенному изменению оптимума целевой функции.
Сформулируем общий принцип, лежащий на основе решения всех задач динамического программирования :
- Выбрать параметры (фазовые координаты), характеризующие состояние S управляемой системы перед каждым шагом.
- Расчленить операцию на этапы (шаги) .
- Выяснить набор шаговых управленийдля каждого шага и налагаемые на них ограничения.
- Определить, какой выигрыш приносит на-м шаге управление, если перед этим система была в состоянии S, т. е. записать”функции выигрыша ” :
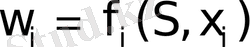
- Определить, как изменяется состояние S системы S под влиянием управленияна-м шаге: оно переходит в новое состояние
- Записать основное рекуррентное уравнение динамического программирования, выражающее условный оптимальный выигрыш:
- Произвести условную оптимизацию последнего(m-го ) шага, задаваясь гаммой состояний S, из которых можно за один шаг дойти до конечного состояния, вычисляя для каждого из них условный оптимальный выигрыш по формуле
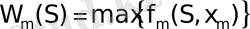
и находя условное оптимальное управление
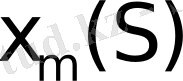 , для которого этот максимум достигается.
, для которого этот максимум достигается.
- Произвести условную оптимизацию (m-1) -го, (m-2) -го и. т. д. шагов, полагая в ней…, и для каждого из шагов указать условное оптимальное управление, при котором максимум достигается.
- Произвести безусловную оптимизацию управления, «читая » соответствующие рекомендации на каждом шаге. Взять найденное оптимальное управление на первом шаге. [6]
- Основная часть
2. 1 Словесная формулировка задачи
Имеется группа предприятий Р 1 , Р 2 …, Р n . В нашем распоряжении какой-то запас средств С, который мы должны распределить между предприятиями так, чтобы получить максимальный доход.
Каждое из предприятий при вложении в него каких-то средств х приносит доход, g i (x), зависящий от вложенных в него средств.
Сумма всех выделяемых средств не должна превышать величину имеющегося капитала. Требуется найти оптимальное распределение ресурсов, при котором суммарная производительность была максимальной.
2. 2 Математическая постановка задачи

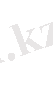
Пусть заданы:
Из N дочерних g
i
(x)
 Equation. 3 i=
Equation. 3 i=
 Equation. 3 ; C.
Equation. 3 ; C.
Необходимо
Ф
n
(х) = mах [g
n
(x) + Ф
n-1
(c-x) ]
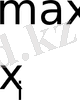 Equation. 3
Equation. 3
 Equation. 3 i=
Equation. 3 i=
 Equation. 3
Equation. 3
При ограничениях:
n = 5;
0
X
C, где 0
С
180[тыс. у. е. ],
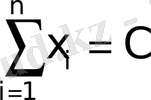
2. 3 Алгоритм
... продолжение- Информатика
- Банковское дело
- Оценка бизнеса
- Бухгалтерское дело
- Валеология
- География
- Геология, Геофизика, Геодезия
- Религия
- Общая история
- Журналистика
- Таможенное дело
- История Казахстана
- Финансы
- Законодательство и Право, Криминалистика
- Маркетинг
- Культурология
- Медицина
- Менеджмент
- Нефть, Газ
- Искуство, музыка
- Педагогика
- Психология
- Страхование
- Налоги
- Политология
- Сертификация, стандартизация
- Социология, Демография
- Статистика
- Туризм
- Физика
- Философия
- Химия
- Делопроизводсто
- Экология, Охрана природы, Природопользование
- Экономика
- Литература
- Биология
- Мясо, молочно, вино-водочные продукты
- Земельный кадастр, Недвижимость
- Математика, Геометрия
- Государственное управление
- Архивное дело
- Полиграфия
- Горное дело
- Языковедение, Филология
- Исторические личности
- Автоматизация, Техника
- Экономическая география
- Международные отношения
- ОБЖ (Основы безопасности жизнедеятельности), Защита труда