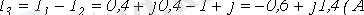Курсовая расчётно-графическая работа (теория электрических цепей)

Тип работы: Курсовая работа
Бесплатно: Антиплагиат
Объем: 17 страниц
В избранное:

КАЗАХСКИЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ
ИМ. ТУРАРА РЫСКУЛОВА

ИНЖЕНЕРНО - ЭКОНОМИЧЕСКИЙ ФАКУЛЬТЕТ

Курсовая расчётно-графическая работа
по дисциплине
“Теория электрических цепей”

Выполнил: Сармурзинов Д., 208 гр.

ИЭФ-05

АЛМАТЫ 2006

Содержание:

1. Теория.
2. Закон Кирхгофа.
3. Метод узловых потенциалов.
4. Задача.
5. Список использованной литературы.

Законы Кирхгофа

Токи, напряжения, Э.Д.С. в разветвленной цепи рассчитываются на основе
правил Кирхгофа. Точка, в которой соединены не менее трех проводников
разветвленной цепи, называется узлом.

Первый закон: алгебраическая сумма сил токов на участках цепи, сходящихся в
любой точке разветвления, равна нулю. Например, на рис. 1

I1
I2
I3

I4

Рис.1 Узел токов

I1 + I2 + I3 - I4=0 (1.1)

Токи, входящие в узел, считаются положительными, токи, выходящие из узла, -
отрицательными.

Второй закон: для любого замкнутого контура, выделенного из разветвленной
цепи, алгебраическая сумма произведений сил токов на сопротивления
соответствующих участков цепи равна алгебраической сумме всех
электродвижущих сил в этом контуре. При составлении указанной суммы
положительными считаются те токи, направления которых совпадают с условно
выбранным направлением обхода контура. Положительными считаются те Э.Д.С.,
которые повышают потенциал в направлении обхода (т.е. направление обхода
совпадает с переходом от отрицательного полюса источника к положительному).
Например, рис.2

Направление обхода

I1R1 + I2R2 – I 3R3 = E1 + E2 – E3 (1.2)

Рис 2. Контур, выделенный из разветвленной цепи.

При последовательном соединении одинаковых источников

I (nRi + R) = nE (1.3)

Где n – число источников, Ri – внутреннее сопротивление одного источника,
R – внешнее сопротивление цепи, Е – Э.Д.С. одного источника.

При параллельном соединении n одинаковых источников

I(R + Rin) = E (1.4)

Два закона Кирхгофа, называемые также правилами Кирхгофа, служат для
расчетов сложных электрических цепей и полностью определяют их
электрическое состояние. Для сложных цепей применяют понятия ветви, узла и
контура. Ветвь электрической цепи – это участок Электрической цепи, вдоль
которого проходит один и тот же ток, и который состоит из последовательно
соединенных элементов – резисторов, источников электроэнергии и т.п. Узел
электрической цепи – это место соединения трех и более ветвей. Контур цепи
– это любой замкнутый путь, который можно обойти, перемещаясь по нескольким
ее ветвям.

Закон Ома для участка цепи с источником ЭДС

Возьмем два участка цепи a-b и c-d (см. рис. 1) и составим для них уравнения
в комплексной форме с учетом указанных на рис. 1 положительных направлений
напряжений и токов.
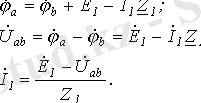        (1.5) 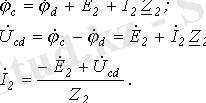       (1.6)
Объединяя оба случая, получим
   (1.7)
(1)

или для постоянного тока
.   (1.8)
(2)

Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи
с источником ЭДС, согласно которому ток на участке цепи с источником ЭДС равен
алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на
сопротивление участка. В случае переменного тока все указанные величины суть
комплексы.
При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с
выбранным направлением тока, и со знаком “ - ”, если их направление
противоположно направлению тока.

Основы символического метода расчета цепей
синусоидального тока

Расчет цепей переменного синусоидального тока может производиться не только
путем построения векторных диаграмм, но и аналитически – путем операций с
комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи.
Достоинством векторных диаграмм является их наглядность, недостатком – малая
точность графических построений. Применение символического метода позволяет
производить расчеты цепей с большой степенью точности.
Символический метод расчета цепей синусоидального тока основан на законах
Кирхгофа и законе Ома в комплексной форме.
Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно
такой же вид, как и соответствующие уравнения для цепей постоянного тока.
Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде
комплексных величин.
1.     Первый закон Кирхгофа в комплексной форме:
. (1.9)
(3)

2.     Второй закон Кирхгофа в комплексной форме:
(2)
(4)

или применительно к схемам замещения с источниками ЭДС
. (2.1)
(5)

3. Соответственно матричная запись законов Кирхгофа в комплексной форме имеет
вид:
         первый закон Кирхгофа:
;   (2.2)
(6)

второй закон Кирхгофа
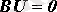(2.3)

Пример. Дано:

Определить:

1) полное комплексное сопротивление цепи

2) токи

Рис. 2

(7)

Решение:
1.     .
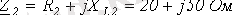2.     .

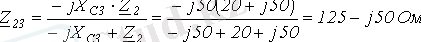3.
                                             .
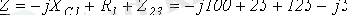
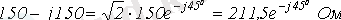4.     Принимая начальную фазу напряжения за нуль, запишем:
.
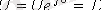Тогда
.

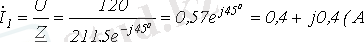5.     Поскольку ток распределяется обратно пропорционально сопротивлению
ветвей (это вытекает из закона Ома), то

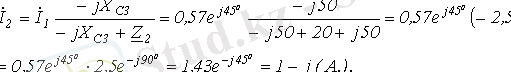
6.     Аналогичный результат можно получить, составив для данной схемы
уравнения по законам Кирхгофа в комплексной форме:

или после подстановки численных значений параметров схемы.

Специальные методы расчета
Режим работы любой цепи полностью характеризуется уравнениями, составленными на
основании законов Кирхгофа. При этом необходимо составить и решить систему с n
неизвестными, что может оказаться весьма трудоемкой задачей при большом числе n
ветвей схемы. Однако, число уравнений, подлежащих решению, может быть
сокращено, если воспользоваться специальными методами расчета, к которым
относятся методы контурных токов и узловых потенциалов.

Метод контурных токов
Идея метода контурных токов: уравнения составляются только по второму закону
Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по
замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей
связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей
связи графа . Первый закон Кирхгофа выполняется автоматически. Контуры
можно выбирать произвольно, лишь бы их число было равно и чтобы каждый
новый контур содержал хотя бы одну ветвь, не входящую в предыдущие. Такие
контуры называются независимыми. Их выбор облегчает использование
топологических понятий дерева и ветвей связи. Направления истинных и контурных
токов выбираются произвольно. Выбор положительных направлений перед началом
расчета может не определять действительные направления токов в цепи. Если в
результате расчета какой-либо из токов, как и при использовании уравнений по
законам Кирхгофа, получится со знаком “-”, это означает, что его истинное
направление противоположно.

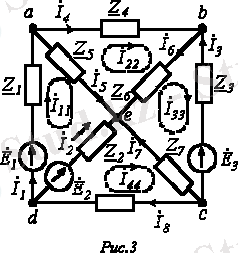
Пусть имеем схему по рис. 3.
Выразим токи ветвей через контурные токи:
;
  ; ;
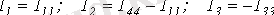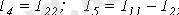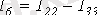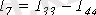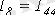  ; . (2.4)
Обойдя контур a-d, по второму закону Кирхгофа имеем
. (2.5)
Поскольку
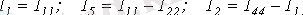(2.6)
то
. (2.7)
Таким образом, получили уравнение для первого контура относительно контурных
токов. Аналогично можно составить уравнения для второго, третьего и четвертого
контуров:
(2.8)

совместно с первым решить их относительно контурных токов и затем по
уравнениям, связывающим контурные токи и токи ветвей, найти последние. Однако
данная система уравнений может быть составлена формальным путем:
(2.9)
При составлении уравнений необходимо помнить следующее:
- сумма сопротивлений, входящих в i-й контур;
- сумма сопротивлений, общих для i-го и k-го контуров, причем    ;
члены на главной диагонали всегда пишутся со знаком “+”; знак “+” перед
остальными членами ставится в случае, если через общее сопротивление i-й
и k-й контурные токи проходят в одном направлении, в противном случае ставится
знак “-”; если i-й и k- й контуры не имеют общих сопротивлений, то ; в
правой части
уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком
“+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и
“-”, если не совпадает.
В нашем случае, для первого уравнения системы, имеем:

Следует обратить внимание на то, что, поскольку , коэффициенты контурных
уравнений всегда симметричны относительно главной диагонали.

Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются
в левых частях уравнений как известные контурные токи: k- й контурный ток,
проходящий через ветвь с k- м источником тока равен этому току .

Метод узловых потенциалов

Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных
принимаются потенциалы узлов, по найденным значениям которых с помощью закона
Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку
потенциал – величина относительная, потенциал одного из узлов (любого)
принимается равным нулю. Таким образом, число неизвестных потенциалов, а
следовательно, и число уравнений равно , т.е. числу ветвей дерева .
Пусть имеем схему по рис. 4, в которой примем .

Допустим, что и известны. Тогда значения токов на основании закона
Ома для участка цепи с источником ЭДС
(3.0)
Запишем уравнение по ... продолжение

Вы можете абсолютно на бесплатной основе полностью просмотреть эту работу через наше приложение.