Ханойские башни

Тип работы: Курсовая работа
Бесплатно: Антиплагиат
Объем: 17 страниц
В избранное:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РЕСПУБЛИКИ КАЗАХСТАН

Казахский национальный технический университет

им. Каныша Сатпаева

Институт информатики и информационных технологий

Кафедра информатики

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовому проекту

Тема: Ханойские башни

Дисциплина - экспертные и интеллектуальные системы

Руководитель

преподаватель

Ахметова М. А.

"___"20__г.

Нормоконтроллер

"___"20__г.

Студент Шигаева К. А. __

Специальность 3704 ___

Группа ПОС-98-5

Алматы 2002

Задание

Название: "Ханойские башни".

Цель: Дано множество начальных состояний, множество операторов, множество конечных состояний. Управляя одним из множества операторов, необходимо создать интеллектуальную программу достижения конечного состояния.

Дата получения задания: 10. 10. 02.

Дата выполнения задания: 20. 11. 02.

Дата защиты КП: .

Содержание

Введение: Введение

3: 3

Введение: 1 Основная часть. .

3: 4

Введение: 1. 1 Методы поиска в пространстве состояний. .

3: 5

Введение: 1. 1. 1 Метод перебора в глубину

3: 5

Введение: 1. 1. 2 Метод полного перебора

3: 5

Введение: 1. 1. 3 Метод оценки вершин. .

3: 6

Введение: 1. 2 Метод сведения задач к подзадачам

3: 7

Введение: 1. 2. 1 Постановка задачи. .

3: 7

Введение: 1. 2. 2 Описание метода. . . . .

3: 7

Введение: 1. 3 "И/ИЛИ" графы. . . . ………. .

3: 10

Введение: 2 Описание алгоритма. . . . .

3: 13

Введение: Заключение. . .

3: 14

Введение: Список литературы. . . . .

3: 15

Введение: Приложение А. Тестирование ……. . . .

3: 16

Введение: Приложение Б. Листинг программы……. .

3: 17

Введение

Курсовой проект посвящен изучению методов разработки интеллектуальных игр на примере игры «Ханойские башни».

Работа по игровым программам развивалась не зависимо от математических исследований в области теории игр. Эти два направления имеют различные цели. Математический анализ игр изучает стратегии, которым должен следовать идеализированный совершенный игрок, а при программировании же действие игрока проходит при определенных ограничениях на использование ресурсов.

Для того, чтобы написать игровую программу, надо решить проблемы представления структуры игр. Эта структура будет связана с методом поиска решения. Человек не задумываясь, использует метод проб и ошибок. Обычно при решении человеком той или иной задачи, он использует в первую очередь, не метод поиска, а ясную точку зрения на рассматриваемую проблему. Поэтому имеется два аспекта решения задач: представление и поиск.

Пока, к сожалению, в исследованиях по искусственному интеллекту еще не выработан универсальный метод для нахождения (искусственных) великолепных формулировок задач. Остается рассмотреть различные методы поиска. Но прежде чем такой процесс поиска начат, сама задача должна быть поставлена в рамках следующих подходов:

подход, основанный на пространстве состояний,
подход, основанный на редукциях подзадач,
подход, как теорема, подлежащая доказательству (исчисление предикатов) .

В качестве постановки задачи мы исследуем подход к решению задач, основанный на сведении задачи к подзадачам.

Чтобы проиллюстрировать этот метод, рассмотрим хорошо известную головоломку "Ханойские башни". Имеются три стержня А, В и С. Вначале на стержень А нанизываем несколько дисков: диск наибольшего диаметра находится внизу, а выше - диски последовательно уменьшающегося диаметра. Цель головоломки - перемещать диски по одному со стержня на стержень так, чтобы диск большего диаметра никогда не размещался выше диска меньшего диаметра и чтобы в конце концов все диски были нанизаны на стержень С.

Данный алгоритм реализован на объектно-ориентированном языке Borland Delphi 6. 0.

1 Основная часть

1. 1 Методы поиска в пространстве состояний

1. 1. 1 Метод перебора в глубину

В методах перебора в глубину прежде всего раскрываются те вершины, которые были построены последними. Определим глубину вершины дерева следующим образом:

глубина корня дерева равна нулю;
глубина любой последующей вершины равна единице плюс глубина вершин, которая непосредственно ей предшествует.

Таким образом, вершиной, имеющей наибольшую глубину в дереве перебора, в данный момент служит та, которая должна в этот момент быть раскрыта.

Такой подход может привести к процессу, разворачивающегося вдоль некоторого бесконечного пути, поэтому нужно ввести некоторую процедуру возвращения. После того как в ходе процесса строится вершина с глубиной, превышающей некоторую граничную глубину, мы раскрываем вершины наибольшей глубины, не превышающей этой границы и т. д.

Метод перебора в глубину определяется следующей последовательности шагов:

Поместить начальную вершину в список, называемый ОТКРЫТ.
Если список ОТКРЫТ - пуст, то на выход подается сигнал о неудаче поиска, в противном случае перейти к шагу (3) .
Взять первую вершину из списка ОТКРЫТ, и перенести ее в список ЗАКРЫТ. Дать этой вершине название n.
Если глубина вершины n равна граничной глубине, то переход в (2), в противном случае к (5) .
Раскрыть вершину n, построив все непосредственно следующие за ней вершины. Поместить их (в произвольном порядке) в начало списка ОТКРЫТ и построить указатели идущие от них к n.
Если одна из этих вершин целевая, то на выход выдать решение, просматривая для этого соответствующие указатели, в противном случае к (2) .

В алгоритме поиска в глубину сначала идет перебор вдоль одного пути, пока не будет достигнута максимальная глубина, затем рассматриваются альтернативные пути той же или меньшей глубины, которые отличаются от него лишь последнем шагом, после чего рассматриваются пути, отмечающиеся последними двумя шагами, и т. д.

1. 1. 2 Метод полного перебора

В методе полного перебора, вершины раскрываются в том порядке, в котором они строятся. Простой алгоритм полного перебора на дереве состоит из следующей последовательности шагов:

Поместить вершину в список, называемый ОТКРЫТ.
Если список ОТКРЫТ - пуст, то на выход подается сигнал о неудаче поиска, в противном случае перейти к шагу (3) .
Взять первую вершину из списка ОТКРЫТ, и перенести ее в список ЗАКРЫТ. Дать этой вершине название n.
Раскрыть вершину n, образовав все вершины, непосредственно следующие за n. Если непосредственно следующих вершин нет, то переход к (2) . Поместить имеющиеся непосредственно следующие за n вершины в конец списка ОТКРЫТ, и построить указатели, ведущие от них назад к вершине n.
Если какие-нибудь из этих непосредственно следующих за n вершин являются целевыми вершинами, то на выход выдать решение, получающееся просмотром вдоль указателя; в противном случае переход к (2) .

В этом алгоритме предполагается, что начальная вершина не удовлетворяет поставленной цели, хотя нетрудно ввести этап проверки такой возможности.

В методе полного перебора непременно будет найден самый короткий путь к целевой вершине при условии, что такой путь вообще существует.

1. 1. 3 Метод оценки вершин

Присваивание дугам деревьев определенных цен (с последующим нахождением решающего пути, имеющего минимальную стоимость) соответствует многим из таких обещанных критериев. Более общий вариант метода полного перебора, называемый методом равных цен , позволяет во всех случаях найти некоторый путь от начальной вершины к целевой, стоимость которой минимальна.

В этом методе для каждой вершины n в дереве перебора нам нужно помнить стоимости пути, построенного от начальной вершины s к вершине n. Пусть g(n) - стоимость от вершины s к вершине n в дереве перебора. В случае деревьев перебора, мы можем быть уверены, что g(n) является к тому же стоимостью того пути, который имеет минимальную стоимость (т. к. этот путь единственный) .

В методе равных цен вершины раскрываются в порядке возрастания стоимости g(n) .

Этот метод характеризуется такой последовательностью шагов:

Поместить начальную вершину s в список, называемый ОТКРЫТ. Положить g(n) =0.
Если список ОТКРЫТ пуст, то на выход подается сигнал о неудаче поиска, в противном случае переходить к следующему шагу.
Взять из списка ОТКРЫТ ту вершину, для которой величина g имеет наименьшее значение, и поместить ее в список ЗАКРЫТ. Дать этой вершине название n. (В случае совпадения значений выбирать вершину с минимальными g произвольно, но всегда отдавая предпочтение целевой вершине. )
Если n есть целевая вершина, то на выход выдать решающий путь, получаемый путем просмотра назад в соответствие с указателями; в противном случае переходить к следующему шагу.
Раскрыть вершину n, построив все непосредственно следующие за ней вершины. (Если таковых нет, переходить к шагу (2) . ) Для каждой из такой непосредственно следующей (дочерней) вершины niвычислить стоимость g(n), положив g(ni) =g(n) +c(n, ni) . Построить эти вершины вмести с соответствующими им только что найденными значениями g в список ОТКРЫТ и построить указатели, идущие назад к n.
Перейти к шагу (2) .

1. 2 Метод сведения задач к подзадачам

Идея такого подхода состоит «в размышлении в обратном направлении» от задачи, которую предстоит решить, с тем чтобы выделить подзадачи, подподзадачи и т. д., пока, наконец, первоначальная задача не будет сведена к набору тривиальных элементарных задач. В подходе, основанном на сведении задачи к подзадачам, используются операторы, которые преобразуют описания задач в описания подзадач. Имеется большое число форм описаний задачи. Для этой цели могут быть использованы списки, деревья, строки, векторы, массивы и другие формы.

Часто удобно описывать задачу на языке элементов представления в пространстве состояний. Любая задача поиска в пространстве состояний может быть представлена как совокупность трех составляющих:

МножествоSначальных состояний.
МножествоFоператоров, отображающих описания состояний в описания состояний.
МножествоGцелевых состояний.

Тогда тройка ( S , F, G) определяет задачу, и она может быть использована как описание задачи. В задаче о пирамидке мы использовали именно это обозначение, хотя, поскольку множество F операторов в пространстве состояний предполагалось одним и тем же для всех задач, в описаниях задачи оно в явном виде не присутствовало.

После того как задачи и подзадачи описаны в виде троек (S, F, G), естественно рассматривать эти подзадачи как задачи нахождения пути между определенными состояниями-вехами в пространстве состояний.

То обстоятельство, что в подходе, связанном с сведением задачи к подзадачам, используются понятия состояний, операторов и целей при описании подзадач, само по себе еще не означает, что этот подход и подход с использованием пространства состояний по существу совпадают. На самом деле, как мы уже отмечали, последовательный перебор в пространстве состояний - это тривиальный случай сведения задачи к подзадачам; по этой причине подход, связанный со сведением задачи к совокупности подзадач, можно рассматривать как более общий метод решения, чем последовательный перебор в пространстве состояний. Можно было бы также рассматривать подход, основанный на сведении задачи к подзадачам, просто как способ перечисления отдельных этапов поиска подпутей между предполагаемыми состояниями-вехами в пространстве состояний и управления процессом компоновки подпутей в полные решения.

1. 2. 1 Постановка задачи

Для того чтобы показать, как можно решать задачу методом сведения к подзадачам, мы воспользуемся головоломкой. Один из вариантов задачи о пирамидке (ханойской башне) можно сформулировать следующим образом:

Имеется три колышка 1, 2 и 3 и три различных диска А, В и С. У дисков в центре имеется отверстие, так что их можно надевать на колышки. Сначала все диски расположены на первом колышке, больший диск С внизу,

Рисунок 1. Задача о "Ханойских башнях"

(слева - начальное состояние, справа - конечное)

а меньший диск А - вверху. Требуется переместить все диски на третий колышек, двигая их по очереди. Перемещать можно всегда только верхний диск, причем нельзя никакой диск помещать выше меньшего. Начальное и целевое расположения, показаны на рисунке 1.

1. 2. 2 Описание метода

Конечно, эта задача может быть решена методами, использующими пространство состояний. Действительно, на рисунке 2 показано полное пространство состояний для этой задачи1. Граф имеет 27 вершин, каждая из которых представляет одно из допустимых расположений дисков на колышках. Обозначение (ijk) у каждой вершины графа описывает такое состояние, когда диск С (наибольший) находится на колышке i, диск В - на колышке j, а диск А (самый маленький) -на колышке k. Если на одном и том же колышке находится более одного диска, то всегда предполагается, что самый большой находится внизу и т. д. Дуги, связывающие между собой пары вершин графа, означают, что некоторый диск может быть переложен так, что конфигурация, представляемая одной из вершин пары, изменится на конфигурацию, представляемую другой вершиной. Например, дуга, идущая от (113) к (123), означает, что (113) можно изменить на (123) посредством перекладывания диска В с колышка 1 на колышек 2. Это действие отражается надписью «Переложить (В, 1, 2) » у этой, дуги. (Путь, выделенный жирными линиями на этом графе, представляет собой решение задачи. )

Задачу о пирамидке можно решить также простым методом сведения задачи к подзадачам. Один из путей сведения исходной задачи о пирамидке, изображенной на рисунке 1, к совокупности более простых задач связан со следующей цепочкой рассуждений:

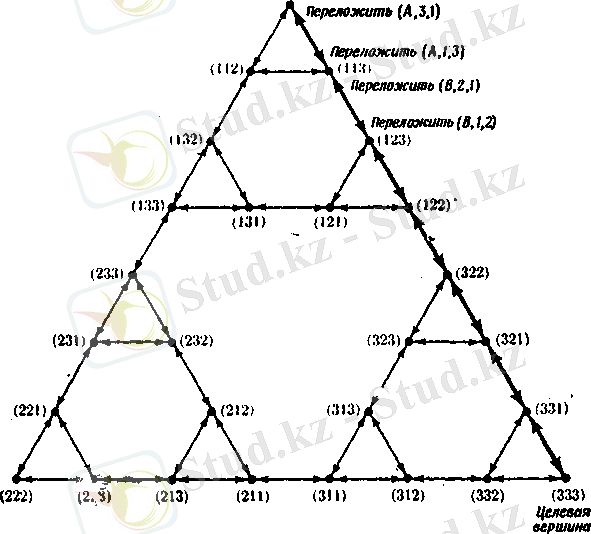
Рисунок 2. Граф для задачи о "Ханойских башнях"

1. Для того чтобы переложить все диски на колышек 3, мы, конечно, должны переложить на этот колышек диск С, причем в момент, непосредственно предшествующий перекладыванию диска С на колышек 3, последний должен быть свободным.

2. Теперь, рассматривая исходную конфигурацию, мы видим, что диск С вообще нельзя никуда переложить, пока с этого колышка не будут сняты диски А и В. Кроме того, диски А и В лучше не размещать на колышке 3, так как тогда у нас не будет возможности поместить там диск С. Таким образом, прежде всего мы должны перенести диски А и В на колышек 2.

3. Затем можно сделать наш основной шаг, переложив диск С с колышка 1 на 3, и перейти к решению оставшейся задачи.

Мы видим, что эти рассуждения позволяют свести исходную задачу к следующим трем задачам:

1. Задача с двумя дисками о перемещении дисков А и В на колышек 2:

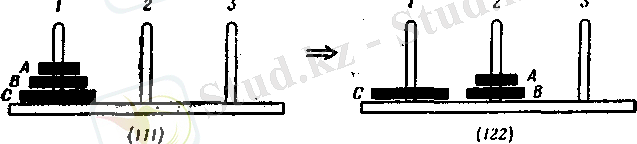
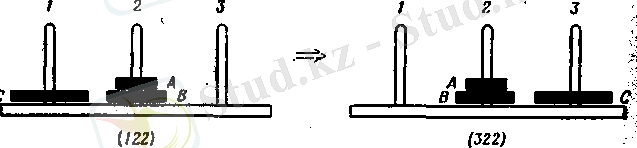
2. Задача с одним диском о перемещении диска С на колышек 3:

3. Задача с двумя дисками о перемещении дисков А и В на колышек 3:

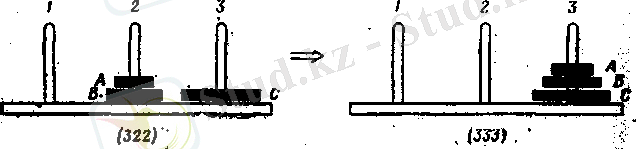
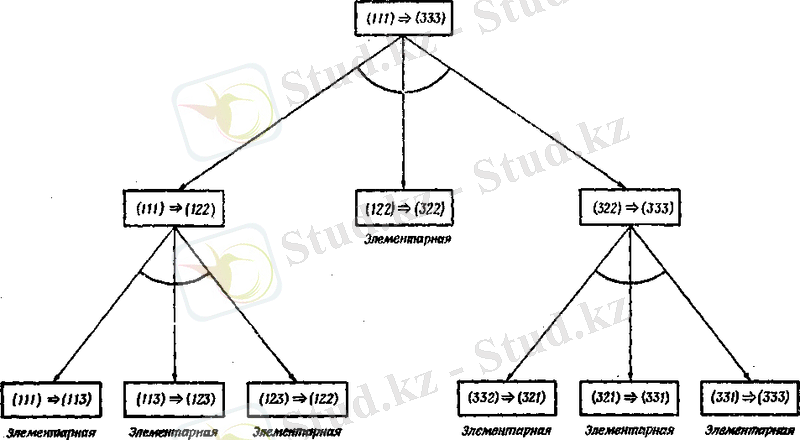
Рисунок 3. Граф подзадач, сводящий задачу о "Ханойских башнях" к совокупности элементарных одношаговых задач

Каждая из этих трех полученных задач меньше, а следовательно, и должна быть легче, чем исходная задача. Действительно, задача 2 может рассматриваться как элементарная, так как ее решение состоит ровно из одного хода. Используя подобную цепочку рассуждений, задачи 1 и 3 также можно свести к элементарным, как это схематически изображено на рисунке 3. (Точно такая же схема сведения задачи к совокупности подзадач может быть применена и в случае, когда начальная конфигурация содержит произвольное число дисков. )

Графовая структура рисунке 3 носит название «И/ИЛИ» графа (или графа подзадач) ; она полезна для иллюстрации решений, получаемых методом. сведения задачи к подзадачам.

1. 3 "И/ИЛИ" графы

Для изображения расчленения задачи на альтернативные множества результирующих задач удобно воспользоваться графоподобной структурой. Так, предположим, что задача А может быть решена либо путем решения задач В и С, либо путем решения задач D и Е, либо путем решения задачи F. Это соотношение изображается структурой на рисунке 4. В вершинах структуры указаны те задачи, которые они представляют.

Рисунок 4. Структура, показывающая различные множества подзадач для А

Рисунок 5. «И/ИЛИ» граф

Задачи В и С составляют одно множество результирующих задач, задачи D и Е - другое, а задача F - третье. Вершины, соответствующие одному множеству, помечены специальным значком, связывающим подходящие к ним дуги.

В структуру обычно вводятся некоторые дополнительные вершины, так чтобы каждое множество, содержащее более одной результирующей задачи, группировалось под своей собственной родительской вершиной. При этом структура на рисунке 4 преобразуется в структуру, изображенную на рисунке 5. На этом рисунке добавленные вершины N и М служат отдельными родительскими вершинами для множеств {В, С} и {D, Е} соответственно. Если считать, что вершины N и М играют роль описаний задач, то мы видим, что задача А сведена к одиночным альтернативным подзадачам N, М или F. По этой причине вершины, помеченные N, М и F, называются «ИЛИ» вершинами.

Задача N сводится к одному множеству подзадач В и С, причем обе они должны быть решены, чтобы была решена задача N. По этой причине вершины, помеченные В и С, называются «И» вершинами. Вершины типа «И» выделяются отметкой, сделанной на идущих к ним дугах.

Структуры, подобные той, что изображена на рисунке 5, называются «И/ИЛИ» графами. Если некоторая вершина "И/ИЛИ" графа имеет непосредственно следующие за ней вершины, то либо все они являются «ИЛИ» вершинами, либо все они - «И» вершины. (Если у некоторой вершины имеется ровно одна непосредственно следующая за ней вершина, то ее можно считать как «И» вершиной, так и «ИЛИ» вершиной. )

Заметим, что в частном случае, когда вершин типа «И» вообще нет, мы получаем обычный граф того типа, который появлялся при переборе в пространстве состояний. Но из-за наличия вершин типа «И» в «И/ИЛИ» графах эти структуры существенно отличаются от обычных графовых структур. Для них требуются свои собственные специализированные приемы поиска, что и служит главной причиной, по которой мы делаем различие между двумя подходами к решению задач.

На языке «И/ИЛИ» графов применение одиночного оператора сведения задачи к подзадачам к некоторому описанию задачи обычно будет означать, что по очереди сначала будет построена промежуточная «ИЛИ» вершина, а затем непосредственно следующие за ней «И» вершины. (Исключение составляет случай, когда множество подзадач состоит из одного элемента. В этом случае образуется ровно одна вершина, а именно «ИЛИ» вершина. )

Таким образом, подходящей структурой, моделирующей метод расчленения задачи на подзадачи, является граф типа «И/ИЛИ». Одна из вершин этого графа, называемая начальной вершиной, соответствует описанию исходной задачи. Те вершины графа, которые соответствуют описаниям элементарных задач, называются заключительными вершинами.

Цель процесса поиска, осуществляемого на «И/ИЛИ» графе, - показать, что начальная вершина разрешима. Общее определение разрешимости вершины в «И/ИЛИ» графе можно сформулировать рекурсивно следующим образом:

... продолжение

Вы можете абсолютно на бесплатной основе полностью просмотреть эту работу через наше приложение.