По дисциплине: Теория нелинейных систем автоматического регулирования

Тип работы: Курсовая работа
Бесплатно: Антиплагиат
Объем: 11 страниц
В избранное:

Республика Казахстан

Алматинский институт энергетики и связи

Кафедра Инженерной кибернетики

Курсовая работа

По дисциплине: «Теория нелинейных систем автоматического регулирования»

Принял:

Профессор

Хисаров Б. Д.

« __ » 2006

Выполнил:

Вертей П. С.

Специальность АиУ

050702

Группа БАУ-04-02

Зачетной книжка № 041168

Вариант №7

Алматы 2007

содержание

Введение: Введение

3: 3

Введение: 1. Задание

3: 4

Введение: 2. Расчетная часть

3: 5

Введение: 2. 1 Определение типов звеньев, входящих в структуру САУ

3: 5

Введение: 2. 2 Определение передаточных функций САУ по задающему воздействию и возмущению, и ее характеристического полинома

3: 5

Введение: 2. 3 Определение устойчивости

3: 6

Введение: 2. 4 Определение граничного значения коэффициента передачи разомкнутой цепи

3: 7

Введение: 2. 5 Расчет статической характеристики САУ

3: 8

Введение: 2. 6 Расчет логарифмических частотных характеристик САУ

3: 9

Введение: 2. 7 Расчет переходных характеристик замкнутой САУ

3: 12

Введение: Заключение

3: 14

Введение: Список литературы

3: 15

введение

Существует чрезвычайно большое разнообразие автоматических систем, выполняющих те или иные функции по управлению самыми различными физическими процессами во всех областях техники. В этих системах сочетаются весьма разнообразные по конструкции механические, электрические и другие устройства, составляя, в общем, сложный комплекс взаимодействующих друг с другом звеньев.

Все автоматические системы делятся на два больших класса: автоматы, выполняющие определенного рода одноразовые или многоразовые операции, и автоматические системы, которые в течение длительного времени нужным образом изменяют какие-либо физические величины в том или ином управляемом процессе.

В данной курсовой работе рассматриваются автоматические системы второго класса, которые делятся на замкнутые и разомкнутые системы. Необходимо выяснить, устойчива ли данная система, и определить показатели качества регулирования. Если система неустойчива, то провести синтез последовательного корректирующего устройства.

Задание

Дана структурная схема САУ в следующем виде:

Рисунок 1 - Структурная схема САУ

1. 1 Определить типы звеньев, входящих в структуру САУ.

1. 2 Определить передаточные функции САУ по задающему воздействию и возмущению, и ее характеристический полином.

1. 3 По критерию Гурвица определить устойчивость САУ.

1. 4 Определить граничное значение коэффициента передачи разомкнутой цепи, при котором САУ теряет устойчивость и построить область устойчивости САУ относительно варьируемых параметров x1 и x2 .

1. 5 Построить статическую внешнюю характеристику для заданной САУ. Рассчитать статизм внешней характеристики.

1. 6 Построить асимптотические и точные ЛАЧХ, точные ЛФЧХ для отдельных звеньев и для системы в разомкнутом состоянии с отображением логарифмической сетки и шкалы. Определить запас устойчивости системы по амплитуде ∆L и фазе ∆ϕ. Сравнить значение ∆L с ранее полученным запасом устойчивости.

1. 7 По характеристическому полиному построить переходную характеристику замкнутой САУ по задающему воздействию g(t) =10В. Определить показатели качества регулирования.

1. 8 Исходя из заданного времени переходного процесса и перерегулирования σ=25% провести синтез последовательного корректирующего устройства и рассчитать переходную характеристику скорректированной САУ по задающему воздействию. Определить показатели качества регулирования для этой САУ и сравнить их с ранее полученными.

Исходные данные (Вариант №7) :

k ₁ = 4 c ^-1 ; k ₃ = 2 c ^-1 ; k _oc = 2 c ^-1 ; T ₁ = 0. 02 c; τ ₂ = 0. 005c; T _oc = 0. 06 c;

Возмущающее воздействие f=10В; варьирующие параметры х ₁ = τ ₂ ; х ₂ = k ₁ ; время переходного процесса t _пп = 0, 195 с.

Расчетная часть

2. 1 Определение типов звеньев, входящих в структуру САУ

В общем случае какой-либо объект в теории автоматического управления описывается передаточной функцией, содержащей полиномы от р произвольного порядка в числителе и знаменателе. Любую САУ можно представить в виде последовательного соединения типовых звеньев, все линейные типовые звенья разделяют на три группы: позиционные звенья, интегрирующие и дифференцирующие.

Звенья W ₁ (p), W _oc (p) относятся к позиционным, а точнее к апериодическим звеньям первого порядка. Их передаточные функции записываются в следующем виде:

Где k ₁ , k _ос - коэффициенты усиления или передаточные коэффициенты, а T ₁ , T _ос - постоянные времени звена.

Звено W ₂ (p) описывается передаточной функцией дифференцирующего звена первого порядка:

Где τ ₂ - постоянная времени дифференцирования.

Звено W ₃ (p) описывается передаточной функцией идеального интегрирующего звена:

2. 2 Определение передаточных функций САУ по задающему воздействию и возмущению, и ее характеристического полинома

Передаточная функция является основной формой математического описания объектов в теории автоматического управления и так как она полностью определяет динамические свойства объекта, то первоначальная задача расчета САУ сводится к определению передаточной функции.

Передаточная функция разомкнутой цепи по задающему воздействию

Передаточная функция разомкнутой цепи по возмущающему воздействию

Передаточная функция замкнутой цепи по задающему воздействию

Передаточная функция замкнутой цепи по возмущающему воздействию

Из передаточной функции W _zg (p) определяем характеристический полином САУ - D(p) и его коэффициенты a ₀ , a ₁ , . . a _n в общем виде.

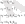
2. 3 Определение устойчивости

Устойчивость заданной САУ должна быть определена алгебраическим критерием Гурвица, т. е. нужно составить главный минор определителя ∆ _n-1 (n - порядок полинома) из коэффициентов характеристического уравнения и проверить выполнение условий устойчивости.

Учитывая, что k ₁ = 4 c ^-1 ; k ₃ = 2 c ^-1 ; k _oc = 2 c ^-1 ; T ₁ = 0. 02 c; τ ₂ = 0. 005c; T _oc = 0. 06 c, мы можем вычислить коэффициенты характеристического уравнения.

∆ ₂ = a ₁ · a ₂ - a ₀ · a ₃

a ₀ = 0. 02·0. 06 = 0. 0012;

a ₁ = 0. 06 + 0. 02 = 0. 08;

a ₂ = 4·2·2·0. 005 + 1 = 1. 08;

a ₃ = 4·2·2 = 16;

∆ ₂ = 0. 08·1. 08 - 0. 0012·16 = 0. 0672;

Так как главный минор определителя ∆ ₂ >0, то заданная система устойчива.

2. 4 Определение граничного значения коэффициента передачи разомкнутой цепи

Для расчета граничного значения коэффициента передачи разомкнутой цепи и построения области устойчивости для параметров х ₁ и х ₂ нужно произвести замену в коэффициентах характеристического полинома фиксированных параметров на варьируемые, введя новую переменную K _raz .

Согласно критерию Гурвица, на границе устойчивости главный минор определителя равен нулю, т. е. нужно решить уравнение ∆ ₂ (x ₁ , x ₃ ) =0 , из которого определится граничное значение коэффициента и выражение для границы устойчивости САУ на плоскости параметров х ₁ и х ₃ .

Граничное значение коэффициента передачи разомкнутой цепи равно 50. Если К<50, то система устойчива; если К>50, то система не устойчива; если К=50, то система находится на грани устойчивости. Так как в нашем случае К = k ₁ ·k ₃ = 8, что меньше 50, то система будет устойчива.

Запас устойчивости по амплитуде ∆L представляет собой запас по коэффициенту передачи разомкнутой цепи по отношению к его граничному по устойчивости значению, в данном случае ∆L=50-8=42

Далее производим замену х ₁ = τ ₂ и х ₂ = k ₁ . И строим область устойчивости для параметров х ₁ ; х _{2 .}

Рисунок 1. - Область устойчивости САУ относительно варьируемых параметров х ₁ ; х ₂

2. 5 Расчет статической характеристики САУ

Внешняя характеристика САУ при изменении возмущающего воздействия от нуля до f _m рассчитывается по передаточным функциям замкнутой САУ при p=0 , то есть по формуле

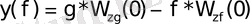g = 10В; f _m = 10В

Статизм внешней характеристики находятся по следующей формуле: .

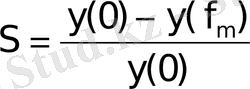Так как статизм внешней характеристики не равен 0, то характеристика статическая, то есть значение выходной величины зависит от величины возмущающего воздействия. На рисунке 2 построена статическая внешняя характеристика для заданной САУ.

Рисунок 2. - Статическая внешняя характеристика для заданной САУ

2. 6 Расчет логарифмических частотных характеристик САУ

Асимптотическая ЛАЧХ разомкнутой цепи САУ строится путем суммирования асимптотических ЛАЧХ ее звеньев.

Общая формула для расчета асимптотической ЛАЧХ инерционного звена (то есть для W ₁ (p) ) :

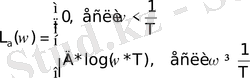
где Т - постоянная времени звена, наклона ЛАЧХ (-20) .

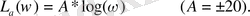Для дифференцирующего звена (то есть для W ₂ (p) ) (при единичном коэффициенте передачи) :

Для идеального интегрирующего звена (то есть для W ₃ (p) ) :

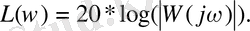
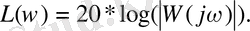Точная ЛАЧХ САУ рассчитывается по формуле:

Точная ЛФЧХ рассчитывается как сумма аргументов от АФЧХ звеньев, составляющих САУ, т. е.

где k - номер звена, n - общее количество звеньев в САУ.

Построим ЛАЧХ и ЛФЧХ в программе MathCad Application. Для этого выводим следующие формулы:

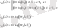
График ЛАЧХ приведен на рисунке 3

Рисунок 3. - ЛАЧХ САУ и отдельных звеньев

График ЛФЧХ приведен на рисунке 4

Рисунок 4. - ЛФЧХ САУ

Построим точные ЛАЧХ и ЛФЧК на отдельном графике (рисунок 5), чтобы определить, устойчива ли наша система.

Рисунок 5. - Совмещенная диаграмма ЛАЧХ и ЛФЧХ САУ

По графику видно, что ЛАЧХ пересекает ось частот раньше, чем ЛФЧХ - линию -π. Следовательно, САУ устойчива согласно критерию устойчивости по логарифмическим частотным характеристикам.

По полученному графику определяем запасы устойчивости по амплитуде (в децибелах) и по фазе (в градусах) . Но запас устойчивости по амплитуде невозможно определить, так как ЛФЧХ не пересекается с линией -180 ^о . А запас устойчивости по фазе ∆ϕ=55 ^о .

2. 7 Расчет переходных характеристик замкнутой САУ

Для расчета переходных характеристик САУ наиболее целесообразным является использование формулы разложения для простых и одного нулевого полюсов изображения выходной величины у

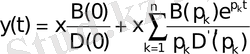
где х - величина входного воздействия, B(p) - числитель передаточной функции, D(p) - знаменатель передаточной функции, D’(p) - производная от характеристического полинома, p _k - k- тый полюс передаточной функции, n - число полюсов передаточной функции.