Процесс совершенствования авиационного оборудования летательных аппаратов

Тип работы: Дипломная работа
Бесплатно: Антиплагиат
Объем: 84 страниц
В избранное:

ВВЕДЕНИЕ

В настоящее время происходит непрерывный процесс совершенствования авиационного оборудования летательных аппаратов в соответствии с постоянно усложняющимися задачами, решаемыми современными авиационными комплексами. Приборное оборудование является важной составной частью бортового авиационного оборудования летательного аппарата. Оно выполняет задачу получения информации о параметрах, характеризующих пространственное положение и движение летательного аппарата в воздушной среде, работу авиационных двигателей и других систем. Эта информация используется для ручного или автоматического управления полетом, для контроля режимов работы силовых установок (СУ), для выполнения задач полета и обеспечения его безопасности.

В понятие «авиационные приборы» включают различные группы приборов, важнейшими из которых являются пилотажно-навигационные, а также приборы контроля работы силовой установки и других систем самолета. Пилотажно-навигационные приборы, в свою очередь, включают в себя аэрометрические приборы, пилотажные гироскопические приборы, навигационные устройства и системы. В процессе своего развития и совершенствования курсовые и навигационные системы выделились в отдельный класс авиационных приборов и измерительных систем. Показания аэрометрических, пилотажных гироскопических приборов, приборов контроля работы силовых установок непосредственно влияют на безопасность полетов. К ним предъявляются особые требования по надежности выдачи информации в аварийных условиях. Поэтому при создании и совершенствовании этой группы приборов стремятся сделать так, чтобы они сохранили свою самостоятельность и автономность, т. е. чтобы работа каждого из этих приборов не зависела от работы других приборов и систем или чтобы эта зависимость, по крайней мере, была минимальной.

Некоторые авиационные приборы входят в измерительные системы и комплексы, и эта тенденция комплексирования усиливается.

Успешное решение задач, связанных с управлением сложными техническими системами и разработкой новых технологий, во многом определяется уровнем развития информационно-измерительной техники. Сроки внедрения научно-технических достижений в различных отраслях деятельности человека также непосредственно связаны с качеством получаемой и анализируемой информации на этапах разработки и доводки изделий. Качество этой информации приобретает особое значение в авиационной технике, где каждый эксперимент в ходе разработки изделий связан с большими временными и экономическими затратами, а получение полной и достоверной информации об объекте исследований позволяет сократить число испытаний и тем самым сроки внедрения образцов новой техники.

1 ГИПОТЕЗЫ И ЗАКОНЫ АЭРОДИНАМИКИ

1. 1. Строение атмосферы

Атмосфера является средой полета различных летательных аппаратов. Она имеет сложное строение, однако условно ее делят на слои с указанием их особенностей. Наиболее характерными и интересными для авиастроителей имеют слои тропосфера, стратосфера, ионосфера и экзосфера [12 - 15, 19 - 20] .

Тропосфера - часть атмосферы, граничащая с Землей (H = 10 - 17 км), где заметно тепловое излучение земной поверхности, где температура заметно уменьшается с удалением от Земли. В тропосфере образуются облака, дуют ветры, тут находится вся испаренная влага, меняется влажность, температура, направление ветра.

На верхней границе тропосферы температура остается постоянной. Далее по высоте располагается стратосфера. В стратосфере температура почти постоянна (~ до 30 км) . Ветры там имеют постоянные направления и направлены против вращения Земли (происходит расслоение нижних и верхних слоев воздуха вследствие малого сцепления частиц воздуха) .

Ионосфера характеризуется наличием свободных ионов и электронов и непрерывным повышением температуры. Границы ионосферы непостоянны (H ≈ до 200 км) .

Экзосфера не имеет вообще границ. Это переходная зона от земной атмосферы к межпланетному пространству (H = от ~ 500 до 1000 км) . Известно что:

50 % массы атмосферы расположено на высотах 0 - 5, 5 км;

75 % массы атмосферы расположено на высотах 0 - 10 км;

94 % массы атмосферы расположено на высотах 0 - 20 км над уровнем моря.

Масса атмосферы составляет 1/1 массы Земли.

Свойства земной атмосферы и происходящие в ней явления изучает наука, называемая метеорологией. Свойства атмосферы используются нами для измерения высоты и скорости полета. От них зависят условия работы пилотов самолетов, тяга двигателя, подъемная сила самолета. Для устранения усложнений в полете (а то и катастроф) необходимо изучение аномальных явлений в атмосфере.

К аномальным явлениям относятся грозы, горизонтальные и вертикальные порывы ветра, турбулентные движения воздуха. Струйные течения воздуха могут быть со скоростью от 100 до 700 км/ч.

Воздух атмосферы является смесью газов: 78 % азота (N ₂ ), 21 % кислорода (O ₂ ), 0, 94 % аргона (A ₂ ), 0, 03 углекислого газа (CO ₂ ), 0, 01 % водорода (H ₂ ) 0, 01 % неона (Ne ₂ ) 0, 01 % гелия (He ₂ ), 1, 2 % пара. На высотах 30 - 50 км имеется озон (O ₃ ) . Максимальное его количество находится на высоте ~ 35 км и составляет 0, 00075 %, тогда как у Земли его только 0, 1 %. Фактически воздух состоит из отдельных молекул газов и не является сплошной средой (особенно на больших высотах) .

Для практических целей авиационные науки нуждаются в установлении закона изменения с высотой основных параметров: как плотность, давление, температура воздуха, скорость звука, вязкость. Но эти параметры зависят еще и от времени года и суток, от случайных явлений в природе. При испытаниях приборов, систем и самолетов требуется проводить сравнение результатов в одинаковых условиях. Так возникла необходимость создания условной стандартной атмосферы (СА), являющейся схемой действительной атмосферы, в которой отсутствуют колебания, вызванные метеорологическими или астрономическими факторами.

На параметры стандартной атмосферы действуют государственные стандарты: ГОСТ 4401-81 (Атмосфера стандартная. Параметры), ГОСТ 3295-73 (Таблицы гипсометрические для геопотенциальных высот до 5 м. Параметры), ГОСТ 5212-74 (Таблица аэродинамическая. Динамические давления и температуры торможения воздуха для скорости полета от 10 до 4000 км/ч. Параметры) и др. [31 - 33] . В отличие от стандартной атмосферы существуют атмосферы справочные, учитывающие широту местности и время года.

В стандартной атмосфере принимаются стандартными исходные параметры: ускорение свободного падения g _с = 9, 80665 м/с ² ; скорость звука a _с = 340, 294 м/с; средняя длина свободного пробега частиц воздуха l _с = 66, 328∙10 ^-9 м; давление P _с = 101325, 0 Па (760 мм рт. ст. ), температура Кельвина T _с = 288, 15 К; кинематическая вязкость ν _с = 14, 607∙10 ^-6 м ² /с; динамическая вязкость μ _с = 17, 894∙10 ^-6 Па∙с; плотность весовая γ _с = 1, 2250 кг/м ³ ; плотность массовая .

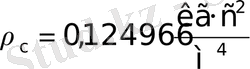Закон изменения температуры воздуха на высотах от нуля до 11000 метров над уровнем моря следующий:

, (1. 1)

где T _н - абсолютная температура воздуха на высоте Н; а - температурный градиент, равный 0, 0065 °С/м; Н - высота над уровнем моря; Т ₀ = 288 °К. Для Н > 11000 м T _н = 216, 5 °К = const. Изменение барометрического давления для высот Н < 11000 м:

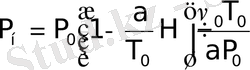, (1. 2)

где P _н - давление на высоте Н; P _о = 760 мм рт. ст. ; ν _о - весовая плотность (1, 2255 кг/м ³ ) ; а - температурный градиент (0, 0065 °С/м) .

Важнейшей характеристикой воздуха является его влажность. Относительная влажность может быть определена по формуле

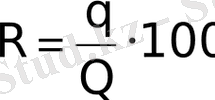, (1. 3)

где R - относительная влажность; q - абсолютная влажность - количество пара в граммах, содержащееся в 1 м ³ ; Q - количество насыщающих паров при данной температуре в г/м ³ .

Предел насыщения воздуха водяными парами в зависимости от температуры приведен в таблице 2. 1.

Таблица 2. 1

t, °С: t, °С

-30: -30

-20: -20

-10: -10

0: 0

+10: +10

+20: +20

+30: +30

t, °С: Q, г/м ³

-30: 0, 5

-20: 1, 0

-10: 2, 5

0: 5, 0

+10: 9, 5

+20: 17, 0

+30: 30, 1

Важно обратить внимание на то, что при понижении температуры воздуха наступает перенасыщение, пар превращается в капли воды [13] . Самолетостроители и разработчики приборов и систем должны это учитывать в своей практике. В связи с этим явлением внутри самолета накапливается большое количество воды, которая пагубно влияет на работоспособность техники.

1. 2. Гипотеза сплошности газовой среды

Теория была введена в практику исследования Даламбером в 1744 году, а затем Эйлером в 1753 году в противовес корпускулярной теории Ньютона.

Воздух атмосферы представляет собой смесь различных газов. До принятия гипотезы сплошности исходили при экспериментах из того, что существует как бы смесь несвязанных между собой молекул газов, между которыми существуют дыры (сито) .

Гипотеза сплошности в аэродинамике основана на том, что расстояние между молекулами воздуха и свободный пробег молекул малы по сравнению с обтекаемым воздухом телом. В связи с этим принимается, что воздух (и вода) однородная, сплошная, без разрывов масса [17, 19, 20] .

Длина свободного пробега молекул зависит от числа молекул в единице объема, т. е. от плотности среды. Мы уже знаем, что вся масса воздуха находится в пределах тропосферы (высота Н ≤ 10…17 км) и что плотность сильно уменьшается с ростом высоты над уровнем моря. У Земли (Н = 0) в одном кубическом миллиметре содержится 2, 7∙10 ⁺¹⁶ молекул воздуха при массовой плотности ρ _о ≈ 0, 125 кг∙с ² /м ⁴ . На высоте Н = 160 км в том же объеме содержится 1 молекула воздуха. А плотность воздуха, например, на высоте Н = 20 км, ρ ₂₀ = 0, 008965 кг∙с ² /м ⁴ .

Длина свободного пробега по высотам в среднем распределяется следующим образом (таблица 2. 2) .

Таблица 2. 2

Н, км: Н, км

0: 0

10: 10

30: 30

62: 62

84: 84

100: 100

120: 120

150: 150

400: 400

Н, км: L _св , см

0: 8, 6∙10 ^-6

10: 2, 1∙10 ^-5

30: 4, 8∙10 ^-5

62: 4, 9∙10 ^-2

84: 0, 5

100: 6

120: 1, 3∙10 ²

150: 2, 0∙10 ³

400: 5, 5∙10 ⁴

Некоторые ученые считают границей применимости гипотезы сплошности отношение длины свободного пробега молекулы воздуха к хорде крыла, равное 1/10 ⁺⁵ .

Кроме плотности воздуха длина свободного пробега зависит от температуры (т. е. от скорости хаотического движения) и от размеров молекул. Средняя длина пробега молекул воздуха рассчитывается по формуле

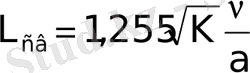, (1. 4)

где К - отношение теплоемкости воздуха при постоянном давлении с _р к его теплоемкости при постоянном объеме с _v , т. е.

;

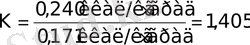ν - кинематический коэффициент вязкости, м ² /с; a - скорость звука в воздушной среде в м/с.

Так как параметры ν и a зависят от высоты над уровнем моря, то и параметр L _св зависит от той же высоты (см. таблицу 1. 2) .

Критерием применимости гипотезы сплошности является число Кнудсена

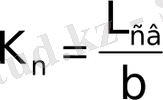или 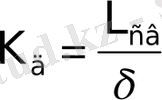, (1. 5)

где b - хорда крыла, δ - толщина пограничного слоя.

Окончательно, или другое значение коэффициента Кнудсена таково:

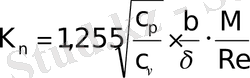, (1. 6)

где М - число Маха, Re - коэффициент Рейнольдса, равный

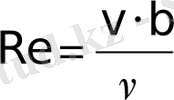, (1. 7)

где v - скорость движения в м/с, b - средняя хорда крыла в метрах, ν - коэффициент кинематической вязкости в м ² /с (рис. 1. 1) .

Практический смысл гипотезы сплошности для специалистов в области приборостроения и самолетостроения состоит с возможности определения границ применения способов измерения воздушных параметров, например, манометрического метода при определении скорости, числа М, подъемной силы.

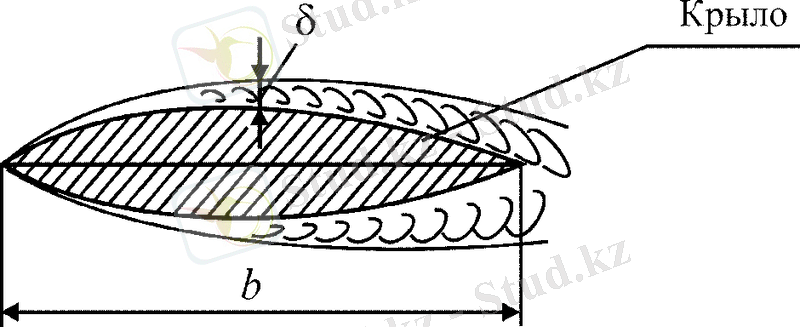
Рисунок 1. 1. Обтекание крыла потоком воздуха

По Ньютону получалось в его корпускулярной теории, что сопротивление движению есть результат ударов частиц о тело и равно:

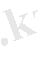
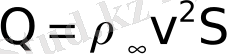, (1. 8)

где ρ _∞ - плотность воздуха; v - скорость движения; S - площадь крыла.

Теперь мы уже будем знать, что формула неверна, она завышает силу сопротивления в два раза.

Область аэродинамики, рассматривающая движение твердых тел в сильно разреженном газе, называется супераэродинамикой [17] .

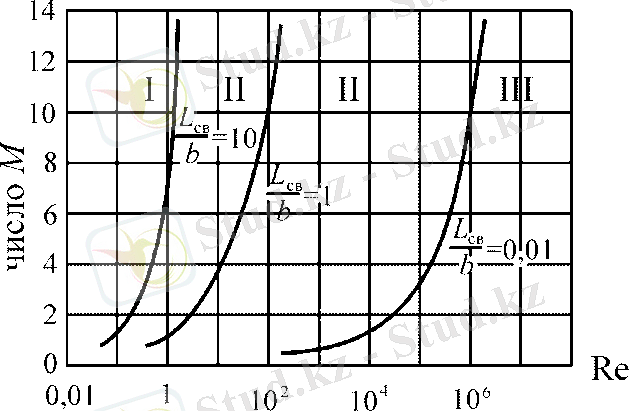
Рисунок 1. 2. Границы областей аэродинамики и супераэродинамики:

I - область супераэродинамики (потоки свободных молекул) ;

II-переходная область - течение со скольжением (вместо полного торможения) ; III-область аэродинамики (газовой динамики, обычные потоки газа с большими скоростями)

Выводы из гипотезы сплошности:

Гипотеза упрощает исследование процессов движения.

Она позволяет рассматривать все механические характеристики жидкой среды - скорости, плотности, давления, числа М и т. д., как функции координат точки и времени. Эти функции предполагаются непрерывными и дифференцируемыми.

Из гипотезы сплошности следуют ограничения применимости методов измерения скоростных параметров. Например, манометрический метод может быть достоверно использован при Н ≈ 3 метров над уровнем моря, при скоростях, соответствующих числу Re = 10 ² …10 ⁷ .

При большом разряжении воздуха и при несоблюдении критерия Кнудсена воздушную среду нельзя считать сплошной. В этих условиях нельзя считать применяемым и принцип непрерывности течения потока воздуха. В этих условиях иными становятся законы образования силы сопротивления движению и подъемной силы. В свободномолекулярном потоке газа единственными силами воздействия газовой среды на движущееся тело являются силы ударов молекул газа о поверхность тела. Величину аэродинамических сил можно оценить по ударной теории Ньютона.

1. 3. Принцип обращенного движения

Принцип обращенного движения говорит о том, что аэродинамические силы не зависят от того, какое из двух взаимодействующих тел (газ или летательный аппарат) покоится, а какое находится в прямолинейном равномерном движении [19, 20] . При этом происходит замена системы: "Неподвижный воздух - движется объект" системой "Неподвижный объект - подвижный воздух". На этом основании считаются справедливыми результаты исследований в аэродинамических трубах. Это справедливо и в случае обтекания тела жидкостью.

Утверждается и обосновывается, что если одно и то же плоское крыло, например, (и сам самолет), обтекается потоком воздуха (жидкости) с одной и той же скоростью и одним и тем же углом атаки, но в противоположном направлении, то подъемная сила Y в обоих случаях будет одной и той же (равной друг другу) .

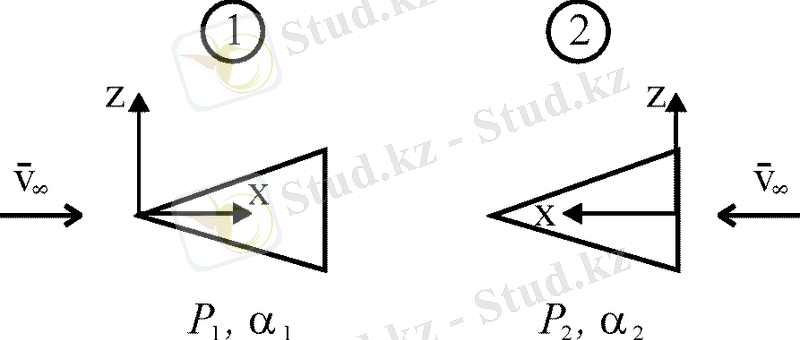
Рисунок 1. 3. Две схемы обтекания тела потоком воздуха:

1-прямой поток; 2-обратный поток

Математически принцип обосновывается следующим образом.

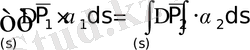, (1. 9)

где 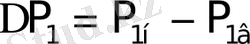, , 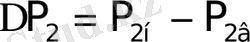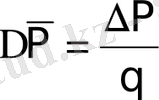- коэффициент давления.

При :

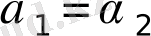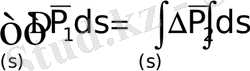, (1. 10)

или

Y ₁ = Y ₂ (1. 11)

На практике могут встретиться многие сложности при применении принципа обращенного движения.

Точно принцип выглядит только теоретически, так как сложно учесть такие факторы как:

- точное достижение равномерности потока по сечению аэродинамической трубы, реки, бассейна;

- влияние стенок трубы, берегов и дна бассейна (реки) ;

- факт искажения потока испытуемым телом. В связи с последним сечение тела должно составлять 3 % и менее по отношению к сечению трубы (бассейна) .

Первые опыты по определению сопротивления при движении проводились в натуральных условиях. Например, Галилей наблюдал падение тел в воздухе с большой высоты. Сопротивление определялось по результатам измерения высоты и времени падения тела. Эйлер (1905 г. ) исследовал падение тела, скользящего по вертикально натянутой проволоке. Для этого использовалась Эйфелева башня. Тело падало с высоты 115 метров со скоростью 40 м/с. Применялся так называемый способ протаскивания, буксировки. Это использовалось для выбора оптимальных форм морского корабля при горизонтальном движении его в воде. Были попытки применения этого метода и при исследовании воздушных моделей, когда модель устанавливалась на движущуюся по рельсам тележку. Но способ при этом был связан с недостатками: ограниченная скорость, влияние тележки на поток воздуха, неравномерность движения тележки. Этот способ остался приемлемым для исследования морских судов, гидросамолетов. Лилиенталь (1874 г. ) и др. использовали естественный ветер для определения силы сопротивления.

В авиации широкое применение нашла аэродинамическая труба, "воздуходувка", по Циолковскому. Известно, что первая труба появилась в 1884 году. К. Э. Циолковский в 1896 -1897 годах начал проводить систематические исследования в аэротрубе. В 1902 году появилась аэротруба Н. Е Жуковского с диаметром 1, 2 м. К аэротрубам предъявляются большие требования. Равномерность скорости должна быть до 1 %, отклонение потока от оси трубы не более 0, 1 %, тело в трубе не должно занимать более 3% рабочей площади трубы.

1. 4. Уравнение неразрывности движения потока

При обтекании тела частицы воздуха совершают сложное движение: поступательное, вращательное и деформационное (меняется форма и объем) . С этим связаны типы обтекания: безвихревое (ламинарное) и вихревое (турбулентное) [20] .

Уравнение неразрывности движения потока в математическом смысле представляет собой закон сохранения массы (основной закон природы) [20] .

Это значит, что масса m в объеме W неизменна, то есть

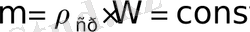, или: 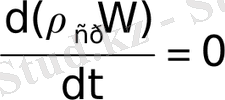. (1. 12)

Однако каждая составляющая ρ и W могут при этом изменяться:

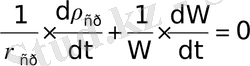. (1. 13)

Последнее выражение и есть общее уравнение теории неразрывности движения потока жидкой среды (воздух, вода и т. п. ) . Частный случай общего уравнения - это установившееся движение, когда 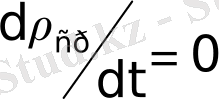. Это относится и к несжимаемой жидкости.

Рассмотрим течение жидкости через отдельную струйку.

Рисунок 1. 4. Течение жидкости через струйку

Количество жидкости, поступающее в единицу времени в объем через торцевое сечение I площадью S ₁ и равное ρ ₁ v ₁ S ₁ , будет таким же, как масса жидкости ρ ₂ v ₂ S ₂ , вытекающая через противоположное сечение II площадью S ₂ , то есть:

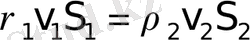или 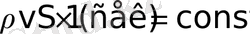, (1. 14)

Последнее уравнение представляет собой уравнение массового расхода жидкости (воздуха), секундный расход. Для контроля определим размерность уравнения массового расхода:

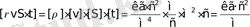- размерность массы в технических единицах. Для несжимаемой жидкости v ₁ S ₁ = v ₂ S ₂ , когд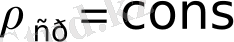а , а .

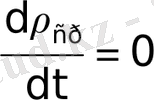Рассмотренная гипотеза практически используется при обосновании характера обтекания тела в потоке, при обосновании формулы подъемной силы крыла, флюгарки ДАУ.

1. 5 Подъемная сила. Теорема Николая Егоровича Жуковского

На рисунке 1. 5 представлено крыло в потоке воздуха, расположенное к оси потока под углом атаки α. Здесь Y - подъемная сила, Q - лобовое сопротивление, которое в 20 - 25 раз меньше подъемной силы Y.

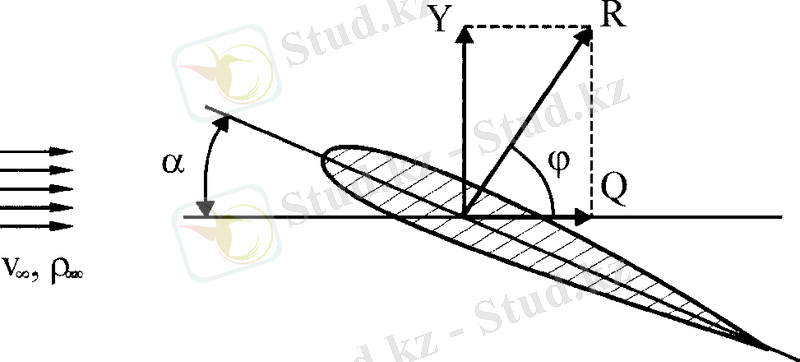
Рисунок 1. 5. Крыло в потоке воздуха

В 1906 году Н. Е. Жуковский для крыла бесконечного размаха доказал теорему о том, что на такое тело (при наличии циркуляции Г вокруг него) действует подъемная сила Y. Закон основан на применении закона количества движения к массам жидкости, обтекающего крыло.

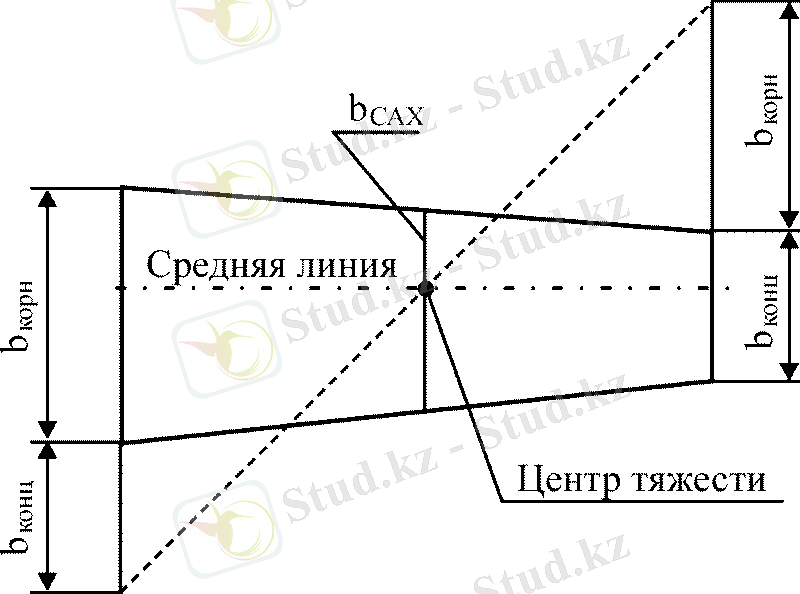
Рисунок 1. 6. Геометрические характеристики крыла: b _корн - корневая хорда; b _конц - концевая хорда; b _САХ - средняя аэродинамическая хорда

Н. Е. Жуковский рассматривал крыло бесконечного размаха, у которого отношения корневой хорды (b _корн ) к концевой хорде (b _конц ) равно бесконечности, то есть при b _конц ≈ 0 или: b _корн / b _конц ≈ ∞ [17, 18, 20, 21] .

Теорема Жуковского формулируется следующим образом: если поток, имеющий в бесконечности скорость v _∞ и плотность ρ _∞ , обтекает цилиндрическое тело (крыло) и циркуляция скорости вокруг этого тела равна Г, то на тело со стороны жидкости будет действовать сила Y, перпендикулярная направлению скорости v _∞ и равная произведению циркуляции на плотность и скорость потока в бесконечности [17] .

Математически теорема Жуковского может быть записана формулой:

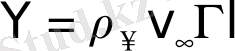, (1. 15)

где l - длина части крыла бесконечного размаха, подъемную силу которой хотят определить.

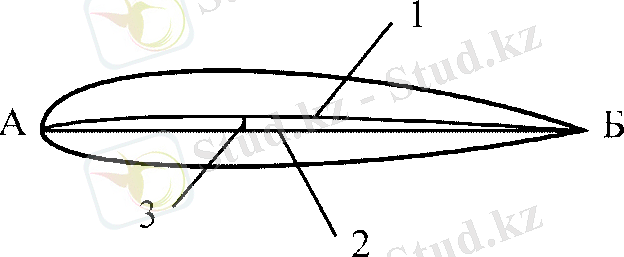
Рисунок 1. 7. Геометрические параметры профиля крыла: 1 - средняя линия; 2 - хорда; 3 - кривизна абсолютная

Величина циркуляции была предложена Жуковским в виде

, (1. 16)

где b - хорда профиля крыла, α - угол атаки крыла в радианах, - относительная кривизна профиля крыла (т. е. отношение кривизны к хорде) .

Подставив последнее выражение (1. 16) в предыдущее (1. 15) получим:

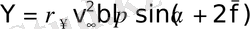, (1. 17)

Положив bl = S (площадь крыла), 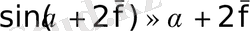в радианах, с учетом того, что суммарный угол 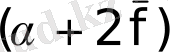обычно не превышает 15˚ ≈ 0, 26 радиана, будем иметь:

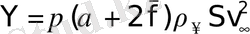, (1. 18)

Как показала дальнейшая практика определения подъемной силы, выведенная теоретическая зависимость не полностью отражает действительность. Связано это с тем, что при выводе не был учтен пограничный слой вокруг крыла. В начале зарождения теории полета практика обгоняла теорию.

... продолжение

Вы можете абсолютно на бесплатной основе полностью просмотреть эту работу через наше приложение.