Изучение различных методов решения задач на построение в пространстве

Тип работы: Дипломная работа
Бесплатно: Антиплагиат
Объем: 46 страниц
В избранное:

СОДЕРЖАНИЕ

ВВЕДЕНИЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .8

1.
Теоритические аспекты при обучении геометрии в общеобразовательной школе, подбор основных тем при изучении геометрии ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... 11

1.1
Основания стереометрии ... ... ... ... ... ... ... ... ... ... ... ... ... .11

1.2
Перпендикулярность и параллельность прямых и плоскостей...16

1.3
Расстояния и угла ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...24

1.4
1.5
2.
2.1
2.2
3.

3.1
3.2
Пространственные фигуры и тела ... ... ... ... ... ... ... ... ... ...27
Многогранники ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .38
Методика преподавания геометрии ... ... ... ... ... ... .. ... ... ..42
Эффективные методы обучения геометрии ... ... ... ... ... ... .. .42
Методика Алгоритм и Воображение ... ... ... ... ... ... ... ..43
Методика решения задач основных глав 10-11 класса на построение в стереометрии с помощью компьютерных программ по геометрии ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... 45
Решения доказательства задач ... ... ... ... ... ... ... ... ... ... ... ... 45
Анализ использования компьютерных программных средств в курсе геометрии ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... 57

Заключение ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ...58

Список использованной литературы ... ... ... ... ... ... ... ... ... ... ... ..61

Приложение(я) ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... .62

ВВЕДЕНИЕ

В стереометрии плоскость - это фигура, на которой выполняется планиметрия, т.е. применяем аксиомы планиметрии и стереометрии. Можно не помнить всех аксиом планиметрии, надо только понимать, что плоскость - это фигура, в которой есть точки, прямые, отрезки, углы с их основными свойствами, а за ними и другие известные фигуры: треугольники, окружности и т.д. Свойствами этих плоских фигур, теоремами о них, доказанными в планиметрии, мы постоянно будем пользоваться.
Важнейшими объектами стереометрии являются пространственные фигуры, не лежащие ни в какой плоскости: например, пирамиды, призмы, куб и т.д.(рис. 1)

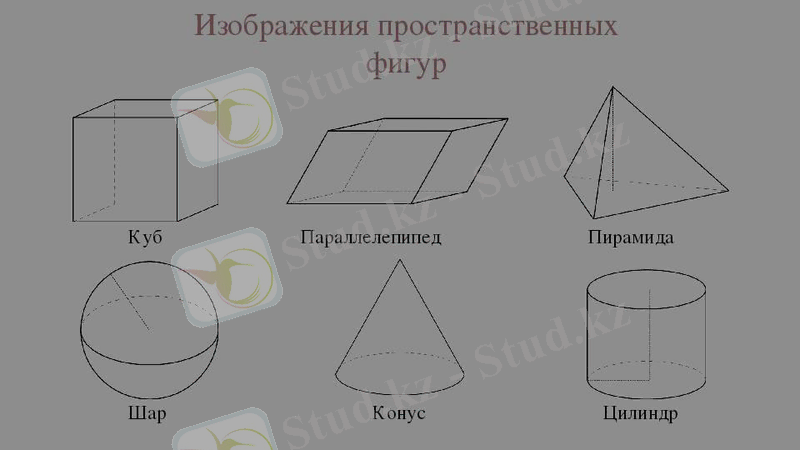
Рисунок 1

Они знакомы нам, но, чтобы изучить их свойства, необходимо сначала рассмотреть взаимное расположение прямых и плоскостей в пространстве.
Актуальность дипломной работы заключается в том, что геометрические построения должны иметь свое личное отражение в школьном курсе геометрии, так как многие ученики имеют пробелы в этой части, особенно это начинается в 10 - 11 классах. Самые сложные задачи связано со стереометрией.
Целью является изучение различных методов решения задач на построение в пространстве.
В связи с этим в данном исследовании решались такие задачи:
1. описать основы задач;
2. показать применение различных инструментов(линейка, циркуль, стёрка и т.д.) при решении таких задач;
3. дать отдельную характеристику к каждой задачи;
4. рассмотреть различные методы решения задач, и выбрать из них наиболее понятный и подробный метод.
Объектом исследования - абстрактная геометрия.
При написании данной дипломной работы применялись следующие методы, как: анализировалась учебное пособие для классов с углубленным изучением математики, проводился поиск и отбор хороших учебников, посвящён на тему: Стереометрия.
В данной работе рассмотрено 5 основных глав из стереометрии, 5 основных программ по геометрии, и методики преподавания геометрии. Так же важно отметить, что разработала две методики при преподавании геометрии. Глава о современной геометрии и теория относительности не рассмотрено. Так как сейчас в школьном курсе убрали эту главу. В основном их обучают в высших учебных заведениях. Во всей главе встречаются одни и те же термины: теорема, аксиома, следствие, лемма и т.д. Остановимся в каждом термине по отдельности.
Аксиома - это правота определенного утверждения, которое не требует доказательств. В основе этих аксиом доказываются все теоремы, которые есть в планиметрии и в стереометрии. В анализе аксиом выяснилось, что в стереометрии существуют всего лишь 5 аксиом. Все аксиомы в основном из первой главы.
Теорема - рассуждения утверждения. То есть рассуждения и есть доказательство утверждения.
Следствие - утверждение, которое само сомой доказывается, с помощью аксиом и теорем. Можно сказать, что это естественный вывод.
Представление о дипломной работе:
Первая глава состоит из основания стереометрии.
Оно состоит из шести тем:
1. Аксиомы стереометрии
2. Способы задания прямых и плоскостей в пространстве
3. Взаимное расположение прямых в пространстве
4. Параллельное проектирование
5. Существование и единственность построения
6. Об аксиомах.
В этой главе основная цель идет объяснить все аксиомы в стереометрии. Но кроме этого встречаются и теоремы. Они такие же легкие и понятные как в планиметрии.
Вторая глава состоит из перпендикулярности и параллельности прямых и плоскостей.
Оно состоит из пяти тем :
1. Перпендикулярность прямой и плоскости.
2. Перпендикулярность плоскостей
3. Параллельные плоскости
4. Параллельность прямой и плоскости
5. Ортогональное проектирование
Третья глава состоит из расстоянии и углов. Это глава состоит из трех тем:
1. Расстояния между фигурами.
2. Пространственная теорема Пифагора.
3. Углы
Четвертая глава состоит из расстоянии и углов. Это глава состоит из шести тем как:
1. Сфера и шар
2. Опорная плоскость
3. Выпуклые фигуры
4. Цилиндры
5. Конусы
6. Тела
Пятая глава состоит из многогранников. Это глава состоит десяти тем как:
1. Многогранники и его элементы
2. Призмы
3. Пирамиды
a. Аксиома плоскости

Теперь можно рассмотреть актуальность геометрических программ в сфере образовании в школе. На сегодняшний день, школьники со второго класса изучают информатику. Это дает гарантию что, школьники в седьмом классе будут готовы к изучению геометрии в виде компьютерных программ. Потому что для инновации новых технологий надо развивать способность мыслить логически, доказывая разные геометрические доказательства. Так как именно доказательство является сложным заданием для школьников. У всех преподавателей разные представления о доказательстве. Из-за этого школьники не имеют точное представление. В связи с этим, все сдачи экзамены для выпускников проходят в виде теста. Эта система дает о себе знать, что выпускники только запоминают формулы, ответы и т.д. Но в основном именно урок геометрии является важной и основной, для выпускников выбирающегося техническую профессию. Ни один урок не развивает мыслительный аппарат как урок геометрия. Предметы, которые в основном опираются на формулу: химия, физика, алгебра.
Анализируя опыт, опыт отечественных и зарубежных коллег по использованию информационных технологий можно сделать вывод о том, что проблема не в отсутствие применение компьютерных программ, а в отсутствие качественного преподавание предмета геометрии:
-отсутствие для учителей и школьников необходимого количества компьютерной техники;
-отсутствие правильного оформления решения задач;
-отсутствие знаний в области компьютерных программ.
1. ТЕОРИТИЧЕСКИЕ АСПЕКТЫ ПРИ ОБУЧЕНИИ ГЕОМЕТРИИ В ОБЩЕОБРАЗОВАТЕЛЬНОЙ ШКОЛЕ, ПОДБОР ОСНОВНЫХ ТЕМ ПРИ ИЗУЧЕНИИ ГЕОМЕТРИИ.

0.1. Основания стереометрии

Определение: фигуры которые лежит на плоскости, к ним применяют аксиомы и теоремы как из стереометрии, так и из планиметрии.
Аксиома 1 (аксиома плоскости) . Плоскость лежащая в пространстве проходит через каждые три точки, которые лежит в пространстве.(рис.1).
Но тут нужно отметить что плоскость существует только в том случае, если в пространстве есть три точки. Если будет существовать по крайней мере четыре точки, которые не лежит в одной плоскости. Соответственно плоскостей будет больше одной. (рис. 2)

Рисунок 2

Далее, из этой аксиомы 1следует, плоскость проходит не только через 3 точки, но может и проходит через одну или две.
Аксиомы о прямой
Аксиома 2 (аксиома пересечения плоскостей). Прямая появившийся при пересечение двух плоскостей, имеют общую точку.

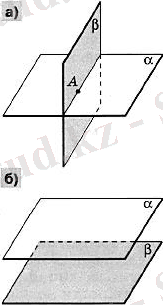
Рисунок 3

Если посмотреть на (рис. 3), то плоскости могут не иметь общих точек, тогда в этом случае они между собой параллельны.
Определение. Пересекающимися плоскостями называются те плоскости, которые имеют общую точку.
Аксиома 3(принадлежности прямой плоскости). Если прямая проходит через две точки данной плоскости, тогда это говорит о том, что она лежит в этой плоскости.
Определение. Если прямая и плоскость имеют единственную общую точку, называются пересекающимися.
Аксиома разбиения пространства плоскостью
Определение. Полупространством, ограниченным плоскостью α, называется фигура со следующими свойствами:
1) она содержит плоскость α, но не совпадает с ней;
2) если точки А и В принадлежит фигуре, но не плоскости α, то отрезок АВ не имеет с α общих точек (рис. 4а)
3) если же точка А принадлежит фигуре, а В нет, то отрезок АВ имеет с α
общую точку (рис. 4б)
Аксиома 4 (аксиома разбиения пространства плоскостью).
Одна плоскость разбивает одно пространство на два полупространства.

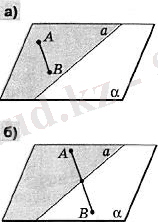
Рисунок 4 (а,b)

Аксиома расстояния
Аксиома 5 (аксиома расстояния).Расстояние двух точек лежащие в пространстве, не зависит от того, лежат ли они в одном и том же плоскости. Если рассмотреть расстояние между точками А и В, то это выражается так: AB
Например: АВ = 3см, 2,5км, 7 или можно записать 7 ед.
Аксиома расстояния дает возможность сравнивать фигуры на разных плоскостях, в основном использовать теоремы о равенстве и подобии треугольников, расположенных в разных плоскостях.

Способы задания прямых и плоскостей в пространстве
Прямая, заданная двумя точками, плоскость, определяемая тремя точками, плоскости, проходящие через прямую.
Прямая, заданная двумя точками
Теорема 1.Через любые две точки лежащие в пространстве, проходит только одна прямая.(рис.5)

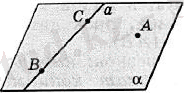
Рисунок 5

Дано: α - плоскость
(А,В) ϵ α
Доказать: (А,В) ϵ а (в пространстве)
Доказательство: По аксиоме из планиметрии( через две точки проходит плоскость α) По аксиоме из планиметрии( через две точки проходит прямая а )
Допустим, (А,В)ϵ а, (А,В)ϵ b. По аксиоме 3(стереометрия), тогда
(a,b) ϵ α. Но в плоскости α выполняется планиметрия, из-за этого в плоскости проходит только одна прямая, тогда в пространстве тоже проходит одна прямая.
Определение: Прямые являются пересекающимися, только в том случае если имеют единственную общую точку.
От этого делаем вывод: Имеем два способа задания прямой в пространстве и в плоскости:
1) двумя точками;
2) двумя пересекающимися плоскостями;
Теорема 2. Плоскость проходит через три точки не лежащие на одной прямой.
Дано: α - плоскость
(А,В,С) ϵ α
Доказать: (А,В) ϵ а (в пространстве), С не лежит на а
Доказательство: По аксиоме из стереометрии (А,В,С) ϵ α
Допустим, (A,B,C) ϵ β -- α∩β,по аксиоме 2 пересечением двух плоскостей является их общей прямой. Но это противоречит условию теоремы , поэтому через А,В,С проходит лишь одна плоскость.
Плоскости, проходящие через прямую
Теорема 3. Одна плоскость проходит через прямую и не лежащую на ней точку.(рис.6)

Рисунок 6

Дано: а ϵ (В,С) , А не лежит на а.
(А,В,С) ϵ α
Доказать: α- одна плоскость
Доказательство: По теорема 2.2 проходит единственная плоскость АВС.
По аксиоме 3, АВС есть искомая плоскость проходящая через прямую а и точку А. В итоге, искомая плоскость единственная.
Теорема 4. Одна плоскость проходит через две пересекающие прямые
Дано: а∩b
(А,В,С) ϵ α
Доказать: α- одна плоскость
Доказательство: По теорема 2.2 проходит единственная плоскость АВС.
По аксиоме 3, АВС есть искомая плоскость проходящая через прямую а и точку А. В итоге, искомая плоскость единственная.

Взаимное расположение прямых в пространстве.
Классификация взаимного расположения прямых в пространстве. Скрещивающиеся прямые, параллельные прямые.
Определение. Две прямые являются скрещивающимися, если не лежат в одной плоскости. (рис.7(а, б, в))

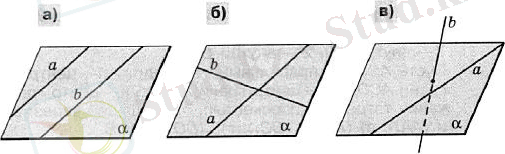
Рисунок 7 (а,б,в)

Две прямые могут иметь три исключающие друг друга возможности:
1. Если две прямые пересекаются, тогда они лежат в одной плоскости.(рис.7б)
2. Если две прямые параллельны, тогда они лежат в одной плоскости и не имеют общих точек.(рис. 7а)
3. Если две прямые не лежат в одной плоскости , тогда они между собой скрещиваются. (рис. 7в)

Рисунок 8

Все три случая можно видеть на примере прямых, в этом комнате (рис. ): например, а скрещивается с b и параллельна с, а b и с -- пересекаются.(рис.8)
Параллельные прямые
Теорема 5. Если точка не лежит на данной прямой, тогда через эту точку можно провести параллельную только одну прямую к данной прямой.
Дано: а - прямая, а ϵ α
А не лежит на а.
Доказать: а⎹⎹ b, bϵA
Доказательство:
По теореме 3 через прямую а и точку А проходит плоскость.
Из планиметрии в плоскости существует прямая b ⎸⎸ a, и проходящая через точку А. В плоскости по аксиоме параллельности есть только одна прямая, проходящая через точку А параллельно прямой а, - прямая b.
Теорема доказано.
Лемма 5. (о пересечении параллельных прямых с плоскостью).
Плоскость пересекает двух параллельных прямых, достаточно чтобы оно пересекало одну прямую.
Теорема 6. Две прямые, параллельные третьей прямой, параллельны.
Дано: а ⎸⎸с, b ⎸⎸c
Доказать: а⎹⎹ b
Доказательство: Допустим, а ∩ b, тогда это противоречит условию теоремы, так как, либо а или b должен быть параллельным к прямой с. Из этого вытекает что а⎹⎹ b.

Параллельное проектирование
Определение параллельного проектирования, основные свойства параллельного проектирования, изображение разных фигур в параллельной проекции.
Даны плоскость α и прямая а которая пересекает эту плоскость. Через произвольную точку X проводим прямую аʹ, параллельную прямой а. Естественно, прямая аʹ пересекает плоскость α в точке Хʹ. Хʹ - называется проекцией точки Х при проектировании параллельной прямой а.(рис.9)

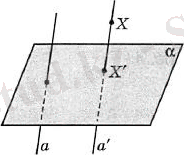
Рисунок 9

Основные свойства параллельного проектирование
Теорема 7. (о параллельном проектировании). Если к прямым провести параллельное проектирование, тогда для лежащих на них отрезков выполняются следующие свойства:
1) Проекция прямой - прямая, а проекция отрезка - отрезок.
2) Проекции параллельных прямых могут быть параллельны или совпадать.
3) Отношение длин проекций отрезков, лежащих на одной прямой
или на параллельных прямых между собой равны.
Дано: α,β - плоскости, α∩b
Доказать: 1) прямая bʹ проекция b, отрезок AʹBʹ проекция AB.
2) bǀǀc проекцией этих прямых только bʹ,или bʹ и сʹ.
3) ABCD=AʹBʹCʹDʹ
Доказательство:
1) a∩b, (a,b)ϵβ-- β∩α = bʹ, bʹ будет проекцией прямой b. Если (X,Y)ϵ β--(Xʹ,Yʹ) ϵ α -- отрезок прямой AB имеет проекцию AʹBʹ.
2) Если bǀǀc, (b,c)ϵβ, l ǀǀ a, l∩c∩b,-- как доказано выше, проекцией прямой b и c является bʹ, по которой β∩α.
3) (A,B,C,D)ϵb, (Aʹ,Bʹ,Cʹ,Dʹ)ϵbʹ, b:bʹ=α∩β, ABAʹBʹ- параллелограмм.
По известной теореме планиметрии параллельные прямые отсекают на двух прямых пропорциональные отрезки, то есть ABCD=AʹBʹCʹDʹ.

1.2 Перпендикулярность и параллельность прямых и плоскостей

Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости. Построение плоскости, перпендикулярной данной прямой. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости. Построение прямой, перпендикулярной данной плоскости. Три взаимно перпендикулярные прямые. О значении перпендикуляра.
Определение перпендикулярности прямой и плоскости.
Перпендикуляр и наклонная
Определение. Прямая является перпендикулярным к плоскости, если оно перпендикулярна к прямой лежащей на этой плоскости.
Теорема 8. (признак перпендикулярности прямой и плоскости). Прямая является перпендикулярным к плоскости, если оно перпендикулярна двум пересекающимся прямым, которые лежат на этой плоскости. (рис. 10)

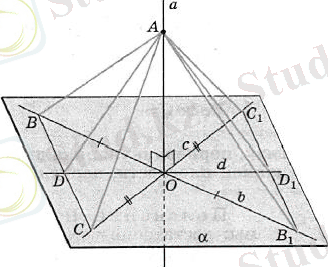
Рисунок 10

Дано: b∩c, а перпендикулярна b, a перпендикулярна c.
αϵ (b,c)
Доказать: a перпендикулярна α
Доказательство: а∩α=О, возьмем что Oϵd, B1ϵ b,C1 ϵ c, -- ВО=ОВ1
СO=OC1, OD1=OD, B1C1=BC, B1D1=BD.
Теперь возьмем аϵА, соединим AB, AC, AD, AB1, AC1, AD1.
Следовательно, точка А равноудалена от концов DD1, O середина отрезка DD1, то прямая а=(АО) является серединным перпендикуляром к отрезку D D1 в плоскости ADD1,т.е. a перпендикулярна d, значит , а перпендикулярна α.
Связь между параллельностью прямых и перпендикулярности прямой и плоскости.
Теорема 9. (о параллели к перпендикуляру). Из двух параллельных прямых, если одна перпендикулярна к плоскости, тогда другая тоже перпендикулярна к этой плоскости.
Дано: aǀǀb, a перпендикулярна α, а∩α=A
Доказать: b∩α
Доказательство: (по лемме 3.1) b∩α=B, Допустим, М∈а, MA- перпендикулярна α,N∈b, MN - перпендикулярна b,-- MNǀǀAB--AMNB - прямоугольник. Из-за этого AB перпендикулярна a, ⎹AB⎹ = ⎹MN⎹=p, MA⎹=⎹MN⎹=h. Теперь через точку B в плоскости α проведем прямус с, что с перпендикулярна к b. Пусть φ - угол между с и b.
Допустим, φ!=90°,Тогда отпустим из точки N перпендикуляр на NC на прямую с. Его длина ⎹NC⎹=h*sinφ.
Позже отпустим прямую из точки М к прямой C. По неравенству треугольника ∆MNC имеем ⎹\MC⎹ = ⎹MN⎹+⎹NC⎹=p+h*sinφ
MA - перпендикуляр к α, МС - наклонная, тогда ⎹MA⎹=h⎹MC⎹
hp+h*sinφ , hp(1-sinφ). Пришли к противоречию. φ!=90°,с перпендикулярно к b.,b перпендикулярно к α.
Следствие(о параллельности двух перпендикуляров) Две прямые являются параллельным, если они перпендикулярны к одной и той же плоскости.
Дано: а∩ α=А, b∩α = B
Доказать: aǀǀb
Доказательство: Через точку А проведем прямую с, параллельную
прямой b. b перпендикулярно к α и cǀǀb, по теореме 7.3 ,с перпендикулярно к плоскости α. Но если через точку А проходят две перпендикулярные прямые а и с к плоскости α, по теореме 7.1 противоречит. Поэтому а ǀǀ b.
Построение прямой, перпендикулярной данной плоскости
Теорема 10. Через каждую точку можно провести одну перпендикулярную прямую к плоскости. (рис. 11)

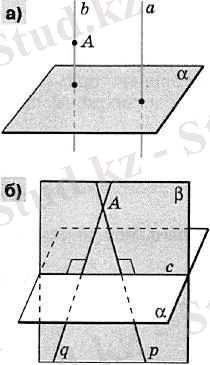
Рисунок 11

Дано:Aϵα
Доказать: c перпендикулярна а(и притом только одна)
Доказательство:Аϵа, Аϵβ,β перпендикулярно к а, то теореме 7.3 -- α∩β= b. Проведем c так: А∈с, с перпендикулярна b и а. Тогда с перпендикулярна к α.(и только одна).

Перпендикулярность плоскостей.
Свойства взаимно перпендикулярных плоскостей. Признак перпендикулярности плоскостей. Две пересекающиеся плоскости, перпендикулярные третьей плоскости.
Свойство 1. Если две плоскости перпендикулярны, и существует одна прямая лежит на одной из этих плоскостей, и перпендикулярна к общей прямой, тогда перпендикулярна к другой плоскости. (рис.12)

Рисунок 12

Дано:α перпендикулярна к β,а перпендикулярна к с.
Доказать: а перпендикулярна к β.
Доказательство:α∪β=с,пусть а∈α и а перпендикулярна к с.
а∩с=О,через точку О в плоскости β проведем прямую b перпендикулярную к с. Тогда а перпендикулярна к β.
Свойства 2. Прямая перпендикулярная двух пересекающимся плоскостям, и при этом имеет общую точку, тогда прямая лежит в одной из них. (рис.13)

Рисунок 13

Дано:α перпендикулярна к β.
А∈а ϵ α,
Доказать: a∈α
Доказательство: с = α∩β, Через точку А в плоскости α проведем прямую l, перпендикулярная к с. Согласно по свойству 1, а и l совпадает. Значит l∈α,a∈α.

Признак перпендикулярности плоскостей
Теорема 11. Две плоскости между собой перпендикулярны, если одна плоскость проходит через перпендикулярную прямую к другой плоскости.
Дано:аϵα, bϵβ, a перпендикулярна к b
Доказать: α перпендикулярна к β
Доказательство: Пусть а перпендикулярна к β, -- а∩β=О, α∩β=с, О∈с, в плоскости β через точку О проведем прямую b перпендикулярна к с. Так как а перпендикулярно к β и b∈β, тогда а перпендикулярно к b -- α перпендикулярно к β.
Теорема 12. Две взаимно перпендикулярные плоскости, перпендикулярны к третьей плоскости, то прямая их пересечения перпендикулярна к третьей плоскости.
Дано:α ⊥ β, α∩β=а, α⊥ γ,
β ⊥ γ.
Доказать: а перпендикулярна к γ.
Доказательство: Через любую точку лежащая на прямой а
проведем прямую, перпендикулярную к плоскости γ. По свойству 2 эта прямая лежит в плоскости α, и в плоскости β. Значит совпадает с прямой а. Итак, а перпендикулярна к γ.
Параллельные плоскости
Первый признак параллельности плоскостей
Теорема 13. Две плоскости между собой параллельны, если оба перпендикулярны к одной прямой.
Дано:а перпендикулярна к α и β.
Доказать: α ǀǀ β
Доказательство: между α и β нет общих точек поэтому они α ǀǀ β.
Леммы о пересечении прямой или плоскости с параллельными плоскостями.
Леммы 13. (о пересечении параллельных плоскостей третьей плоскостью.) Когда двух параллельных плоскостей, пересекает третий плоскость, две прямые которые образовались при пересечении, между собой параллельны. (рис.14)

Рисунок 14

Дано:αǀǀβ,γ∩α=а,γ∩β=b.
Доказать: aǀǀb
Доказательство: (a,b)∈γ,они не имеют общих точек так как лежат
в плоскостях α и β. Поэтому параллельны aǀǀb.
Леммы 14. (о пересечении прямой с двумя параллельными плоскостями). Если прямая пересекает одну параллельную прямую, тогда и пересекает другую прямую. (рис.15)

Рисунок 15

Дано: αǀǀβ,γ∩α=а,γ∩β=b. с∩α=А.
Доказать: с∩β=В
Доказательство: Возьмем точку С на плоскости β--С∈b.
По лемме 13 прямые aǀǀb, из аксиомы параллельности с∩b=B,тогда
с∩β=В.

Параллельные плоскости
Признак параллельности прямой и плоскости. Второй признак параллельности плоскостей.
Теорема 15. (признак параллельности прямой и плоскости) Прямая не лежащая в плоскости параллельна к прямой лежащая в плоскости, тогда не лежащая прямая параллельна к плоскости. (рис.16)

Рисунок 16

Дано: аǀǀb,bϵα
Доказать: aǀǀα
Доказательство: Если а пересекает плоскость α, по лемме 5 b∩α
Но не пересекает поэтому а не пересекает α, тогда аǀǀα.
Второй признак параллельности плоскостей
Теорема 16. Если две прямые лежат в разных плоскостях, и параллельны к дуг другу, тогда плоскости содержащие эти прямые параллельны. (рис.17)

Рисунок 17

Дано: αϵa,b,βϵ(a,b),b1ǀǀb, a1ǀǀa.
Доказать: αǀǀβ
Доказательство:а1∩b1=О, Теорема 15 прямые a1 и b1 лежат в плоскости α и проходящей через точки О.
Поэтому βǀǀα.

Ортогональное проектирование
Метод Монжа и начертательная геометрия.
Самый важный способ проектирования именно в пространстве - ортогональное проектирование.(ортогональное проектирование в переводе как прямоугольный)
Ортогональной проекцией точки на прямую это- основание перпендикуляра , опущенного из точкой не лежащую на данной прямой (плоскости).
Ортогональной проекцией фигуры на прямую (на плоскость) - множество ортогональных проекций всех точек от заданной фигуры на прямую.
Теорема 17. (о проекции на прямую). Ортогональной проекцией одной точки на одну прямую называется точкой пересечения прямой с плоскостью, проведенной через точку перпендикулярно прямой . Другими словами, проектирование на прямую можно производить по перпендикулярным ей плоскостям (вместе перпендикулярных прямых). (рис.18)

Рисунок 18

Дано:αϵА, α∩а
Доказать: , α∩а = Аʹ, ААʹ- перпендикуляр.
Доказательство: от предыдущих теорем через прямую А к прямой а, можно провести только один перпендикуляр, А∈а,тогда А=Аʹ, если А не лежит на а, тогда ААʹ-перпендикуляр.
Лемма 17. (о проекции отрезка). Ортогональной проекцией отрезка на плоскость это отрезок, если отрезок перпендикулярен плоскости, - в этом случае его ортогональная проекция точка.
Ортогональной проекцией отрезка на прямую является отрезок , за исключением того случая, когда данный отрезок лежит в плоскости, перпендикулярной данной прямой, - в этом случае проекцией отрезка является точка.
Дано:αϵ(А,В), α∩а, ААʹ- перпендикуляр,ВВʹ- перпендикуляр
Доказать: Ортогональная проекция АВ является Аʹ=Вʹ
Доказательство: По теореме 17. А и В не лежит на прямой а, поэтому они перпендикулярны. А перпендикулярно к плоскости α, в точке Аʹ, В перпендикулярно к плоскости α в точке Вʹ. Тогда Ортогональная проекция АВ является Аʹ=Вʹ.
Начертательная геометрия была создана знаменитым французском математиком Гас Паром Монжем. Дано ортогональная проекция плоскостей α1 и α2. α1 перевернем вокруг прямой х , до совпадения с α2. После этого они изобрязятся на одном и том же чертеже и называется эпюром.
Прямая х - называется осью проекции.(рис.19)

Рисунок 19

1.3. Расстояния и углы

Определение. Расстоянием от точки А до фигуры F называется расстояние от этой точки до ближайшей к ней точки фигуры (если есть такая точка в фигуре F).
Это расстояние будем обозначать ⎸AF⎸.
Ближайшая к А точка фигуры F - это такая точка B∈F, что для всех точек Х фигуры F. ⎸AB⎸= ⎸AX⎸(рис.20)

Рисунок 20

Рассмотрим три утверждения:
1. Расстояние от центра окружности до самой окружности равно радиусу.
2. Расстояние от точки А до прямой а равно длине перпендикуляра, опущенного из А на а.
3. Расстояние от точки до плоскости это является длиной перпендикуляра, опущенного из этой точки на плоскость.
Теорема о ближайшей точке
Лемма 18. Если А - данная точка, В - ее проекция на плоскость α, то для
любой точки Х ∈α, ⎸AX⎸2= ⎸AB⎸2+⎸BX⎸2
Дано:α - плоскость,(Х,В)ϵα, В проекция точки А.
Доказать: ⎸AX⎸2= ⎸AB⎸2+⎸BX⎸2
Доказательство: Если А∈α, то А=В и ⎸АВ⎸= 0.(верно)
А не лежит α, АВ - перпендикуляр, АВХ - прямоугольный треугольник.
Из теоремы Пифагора, если Х=В, то ⎸ВХ⎸ = 0, и равенство тоже верно.
Теорема 18. (о ближайшей точке). Если точка фигуры ближайшая к проекции данной точки на плоскость фигуры , тогда точка плоской фигуры является ближайшей к некоторой точке.
Дано:Fϵα, (X,C,F)ϵα
Доказать: Расстояние к ближайшей точке - ⎸АВ⎸
Доказательство: Пусть Аϵα, В - проекция точки А на плоскость α,
XϵF, по лемме 18 ⎸AX⎸2= ⎸AB⎸2+⎸BX⎸2от сюда вытекает что расстояние к ближайшей точке - ⎸АВ⎸.
Лемма 19. Параллельные отрезки с концами на двух параллельных плоскостях равны.
(рис.21)
Рисунок 21

Пространственная теорема Пифагора.
Пространственная теорема Пифагора для проекций
Теорема 20. (пространственная теорема Пифагора).
Квадрат длины любого отрезка равен сумме квадратов длин его проекций на любые три взаимно перпендикулярные прямые. (рис.22)

Рисунок 22

Дано: а∩b∩c, γϵ(a,b)
Доказать: AB2=A1B12+A2B22+A3B32
Доказательство: Через точки А и В проведем перпендикулярные прямые p и q на плоскость α, АʹВʹ ϵγ- проекция отреза АВ.(если p=q (АВ) ǀǀ с). У нас p перпендикулярно к γ и q перпендикулярно к γ, тогда pǀǀq, (p,q)ϵβ. Возьмем отрезок АС, оно перпендикулярно к ВС. АʹВʹ=АС - проекция отрезка АВ.
А1В1ϵа, A2B2ϵb, A3B3ϵc
AʹBʹ2=A1B1ʹ+A2B22
По теореме 18 следствие 1, АС=A3B3, : AB2=A1B12+A2B22+A3B32.

Углы
Угол между лучами. Угол между прямыми. Угол между прямой и плоскостью. Двугранный угол. Угол между плоскостями.
Даны две прямые, и один из них лежит другая прямая или они лежит на параллельных прямых по одну сторону от прямой, проходящей через их начала то они являются со направленными или одинаково направленными прямыми.
Лемма 21. Углы, стороны которых соответственно со направленны,
равны. (рис.23)

Рисунок 23

Дано: О - точки. p↑↑pʹ, q↑↑qʹ
Доказать:pʹqʹ=pq
Доказательство: OA = ОʹАʹ и ОВ=ОʹВʹ, проведем отрезки ООʹ,ААʹ,ВВʹ,АВ,АʹВʹ, если они равны то соответсвенно ǀǀ. Тогда ОААʹОʹ - параллелограмм
АВВʹАʹ - параллелограмм
Следовательно АОВ=АʹОʹВʹ,тогда :pʹqʹ=pq
Угол между двумя пересекающимися плоскостями равен двум пересекающимися прямыми которые лежит в этих плоскостях. (рис.24)

Рисунок 24

1.4. Пространственные фигуры и тела

Определение. Сферой является множество точек пространства, удаленных от данной точки на заданное положительное расстояние. При этом данная точка называется центром сферы, а расстояние - ее радиусом.( на рисунке О является центром сферы, ОХ=R радиусом сферы.)
Определение. Шаром называется множество точек пространства, находящихся от данной точки на расстоянии, не большем некоторого данного положительного расстояния. Указанная точка называется центром шара, а указанное расстояние - радиусом шара. (рис.25)

Рисунок 25

Пересечение шара и сферы с плоскостью
Теорема 23. (о пересечении шара и сферы с плоскостью).
1) Если расстояние от центра шара до данной плоскости больше радиуса шара, то плоскости не имеет с шаром общих точек
2) Если расстояние от центра шара до плоскости равно радиусу шара, то плоскость имеет с шаром и ограничивающей его сферой только одну общую точку
3) Если расстояние от центра шара до плоскости меньше радиуса шара, то пересечение шара с плоскостью представляет собой круг. Центр этого круга находится в основании перпендикуляра, опущенного из центра шара на плоскость, или в самом центре шара, если плоскость проходит через центр. Пересечение плоскости со сферой представляет окружность указанного круга. (рис.26)

Рисунок 26

Дано: О - центр шара, R-радиус, ⎸Оα⎸= ⎸ОA⎸= d
Доказать: ⎸Oα⎸= dR, ⎸Oα⎸= d = R, ⎸Oα⎸= dR
Доказательство:
1) ⎸Oα⎸= dR, есть точка Х и для этого выполняется: ⎸OX⎸=dR, отсюда вытекает α нет точек.
2) ⎸Oα⎸=d=R, ⎸OA⎸=R, есть точка Х и для этого выполняется:
⎸XO⎸R,поэтому на α лежит только одна точка - А.
3) ⎸Oα⎸= dR, r=R2-d2 для этого докажем два утверждения:
1. Каждая общая точка шара и плоскости принадлежит указанному кругу.
2. Каждая точка указанного круга является общей точкой шара и плоскости.
OX2=OA2+AX2=d2+AX2, тогда OX=R-- OX2= R2. Из-за этого d2+AX2=R2 отсюда вытекает AX2=R2-d2 или AX=R2-d2 отсюда вытекает
AX и есть радиус, AX=r.
Касание шара и сферы с плоскостью
Теорема 24. (о касании сферы и плоскости). Если плоскость касается сферы, то она перпендикулярна радиусу, проведенному в точку касания. Обратно, если плоскость проходит через точку сферы и перпендикулярна радиусу, проведенному в эту точку, то она касается сферы.
Не требует доказательств.
Сфера вписана в многогранник, если касается всех граней, от сюда вытекает многогранник описан около сферы.
Сфера описана около многогранника, если проходит через вершины, тогда многогранник вписан в сферу.
Проекция шара, как и сферы, есть круг того же радиуса.
Если проекции фигуры на все плоскости - круги, то фигура эта - сфера в объединение с некоторым множеством внутренних точек.
Углы сферического треугольника равны соответствующим двугранным углам того трехгранного угла, который вырезает из сферы данный сферический треугольник.
Выпуклые фигуры
Фигура называется выпуклой , если она содержит соединяющий отрезок, вместе с двумя точками.
Теорема 25. Пересечение любых двух выпуклых фигур остается неизменным выпуклой фигурой, пересечение любой совокупности выпуклых фигур выпукло.
Теорема не требует доказательств.
Теорема 26. Проекция выпуклой фигуры на плоскость называется выпуклой фигурой. (рис.27)
Берілген: Фигура - F
Дәлелдеу: Фигура - Fʹ дөңес
Дәлел: F дөңес фигура болсын, Fʹ - α - дағы проекциясы, (А,В)⊂F-- (Аʹ,Вʹ)⊂Fʹ. Онда Fʹ -дөңес фигура

Рисунок 27

Цилиндры. Определение и свойства цилиндра. Прямой круговой цилиндр. Выпуклые цилиндры
Цилиндр встречается во всей форме. Например трубы, шайбы и т.д.
Пусть дано произвольная фигура на плоскости α, и берем точку А. К плоскости α нарисуем проекцию αʹ.Внутри фигуры F нарисуем точку Х. И к фигуре, ко всем точкам нарисуем соответствующую проекцию. Тогда появится цилидр, плоская фигура F называется основанием цилиндра. А отрезки XXʹ-образующими. (рис.28)

Рисунок 28

Все сечения цилиндра плоскостями, параллельными плоскости основания, равны основаниям цилиндра и между собой.
Если две прямые , перпендикулярные одной плоскости, параллельны, то все высоты цилиндра параллельны, а так как высоты лежат между параллельными плоскостями, то такие высоты не только параллельны, но и равны друг другу. (рис.29)

Рисунок 29

Поверхностью прямого кругового цилиндра - это объединение его оснований и боковой поверхности. Можно сказать любое сечение прямого кругового цилиндра такой плоскостью есть круг, а сечение его боковой поверхности - окружность этого круга. (рис.30)

Рисунок 30

Выпуклые цилиндры
Теорема 27. Цилиндр является выпуклым при одном случае, когда его основание выпукло.
Дано:αǀǀβ, αϵ(Xʹ,Zʹ,Yʹ), βϵ(X,Z,Y), AB∈XXʹYYʹ
Доказать:1) Если цилиндр выпуклый, то его основание выпукло.
2) Если основание цилиндра выпукло, то и сам цилиндр выпуклый.
Доказательство:1) Первое утверждение вытекает от следствии 1 теоремы 25. 2) Пусть С выпукло, возьмем внутри цилиндре две точки А и В проведем из них образующие XXʹ и YYʹ и ZZʹ. Так как отрезок АВ внутри в параллелограмме XXʹYYʹ , тогда АВ содержится в С. Значит цилиндр С выпуклый. (рис.31)

Рисунок 31

Конусы. Усеченные конусы
Теорема 28. (о сечении конуса). Пусть плоскость пересекает конус и параллельна плоскости его основания. Сечение конуса такой плоскостью подобно основанию конуса. Коэффициент подобия равен отношению расстояния от вершины конуса до плоскости сечения к высоте конуса. (рис.33)

Рисунок 33

Дано:P- вершина конуса, Fϵα
Доказать:αǀǀαʹ, F~Fʹ,k=POʹPO
Доказательство: Пусть Fʹϵαʹ, P и F лежат по разные стороны от αʹ, иначе она не ... продолжение

Вы можете абсолютно на бесплатной основе полностью просмотреть эту работу через наше приложение.