Оптимизация использования производственных мощностей металлургического завода методом линейного программирования (симплекс-метод)


Тип работы: Реферат
Бесплатно: Антиплагиат
Объем: 25 страниц
В избранное:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РК
Казахский национальный технический университет
им. К. И. Сатпаева
кафедра технической кибернетики
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе по дисциплине
«Теоретические основы компьютерных систем»
Тема: «Оптимизация использования производственной мощности»
Руководитель
профессор
О. П. Волобуева
“”2004г.
Нормоконтроллер
Ф. И. О.
“”2004г.
Студентка ___Габдуалиева Н. М.
Специальность 370140
Группа КСУ-01-3
“”2004г.
Алматы 2004
Индивидуальное задание
на курсовую работу по дисциплине
"Теоретические основы компьютерных систем".
На металлургическом заводе изготавливается сталь n марок {X 1 , X 2 , …, X n }; сталь изготавливается последовательно в m цехов завода. Производственная мощность каждого из цехов определяется временем обработки одной тонны каждой марки стали и общим временем возможной работы конкретного цеха в определенном периоде. По ней определяются ограничения, составляющие основу модели задачи.
Критерием оптимальности является максимальный общий объём выпуска продукций в денежном выражении:
Z (X) =
. 3
. 3
При ограничениях:
X i
. 3 0,
. 3; (1)
вида В (2)
1) Найти оптимальные значения объёма выпуска марок стали X i ,
. 3.
2) Провести моделирование на PC и сравнить полученные результаты с расчетными.
Исходные данные приведены в таблице.
Таблица 1-Данные для решения задачи
Коэффициенты целевой
Функции а i
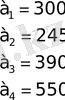
x 1 + 2x 2 + x 3 + 4x 4 ≤ 30; x 1 ≤ 3;
2x 1 + 2x 2 + x 3 + x 4 ≤ 40; 2x 2 ≤ 7;
2x 1 + x 2 + 2x 3 + x 4 ≤ 50; 3x 3 ≤ 18;
x 1 + x 2 + x 3 + 2x 4 ≤ 60; x 4 ≤ 2;
Руководитель работы Волобуева О. П. И. О. Ф.
подпись
Задание приняла к исполнению Габдуалиева Н. М. И. О. Ф.
"__" 2004 г.
подпись
Дата предоставления готовой работы к защите ""2004г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. …. 4
1ОБЩЕЕ РЕШЕНИЕ ЗАДАЧИ . . . . . . …. … . . . 5
1. 1 Выделение элементарных актов, выбор и обоснование
целевой функции5
1. 2 Разработка общей математической модели и формулирование задачи оптимизации. . . ………. . . . …5
1. 3 Модифицированные жордановы исключения (МЖИ) . . ……. . 6
1. 4 Алгоритм прямого симплекс-метода. . . . . . ……6
1. 5 Алгоритм двойственного симплекс-метода. . 8
2 РЕШЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ . . . 10
2. 1Содержательная формулировка задачи. . . 10
2. 2Построение математической модели 10
2. 3Выбор метода и разработка вычислительного алгоритма решения задачи . . 11
2. 3. 1Решение прямым симплекс-методом. . 11
2. 3. 2Решение двойственным симплекс-методом . . . 13
3 ПРОГРАММНАЯ РАЗРАБОТКА . . . . … 15
3. 1Общие сведения. 15
3. 2 Функциональное назначение. . 15
3. 3Описание программного продукта . . . 15
3. 4 Описание программы. . 15
ЗАКЛЮЧЕНИЕ . . . . . 17
СПИСОК ЛИТЕРАТУРЫ18
ПРИЛОЖЕНИЕ А. . 19
ПРИЛОЖЕНИЕ В. . . ………21
ВВЕДЕНИЕ
Совершенствование управления системами самого различного вида является одной из наиболее актуальных проблем во все времена.
Естественный ход развития науки управления - от простого к сложному. Сначала автоматическое управление простейшими техническими системами, затем оптимальное управление сложнейшими технологическими процессами и такими сложными системами, как современный самолет, корабль, космический аппарат. И только в последнее время наука управления организационными системами сильно шагнула вперед в своем развитии, благодаря целенаправленной деятельности самих элементов организационных систем, бурному применению ЭВМ и применениям новых информационных технологий.
К настоящему времени управление организационными системами в большей мере рассматривается в экономике и производстве. Под механизмами функционирования таких систем понимаются, как правило, процедуры формирования информации для управления, методы формирования управляющих переменных (объем ресурсов, продукции, цен, нормативов), методы финансового управления и экономического стимулирования, административные и финансовые ограничения на деятельность фирм и их дочерних предприятий, методы оперативного управления, методы создания конкуренции и т. д. -в общем, набор организационных, правовых, экономических, финансовых правил, регламентирующих функционирование фирм в экономике и производстве. [2]
К задачам управления организационными системами относятся задачи оптимизации, которые можно решить с помощью симплекс-метода, разработанного Дж. Данцигом в 1947 г. Необходимость создания методов решения оптимизационных задач достаточно ясно осознавалась уже и раньше, в частности экономистами и военными специалистами, которым во время второй мировой войны приходилось искать пути решения сложных задач, возникавших при планировании стратегических операций.
Важность разработанного Данцигом симплекс-метода стала еще более очевидной после того, как основоположником теории игр Дж. Нейманом в 1947 г. была развита концепция двойственности. Это открыло путь исследованиям по многим направлениям ЛП, что обеспечило в дальнейшем увеличение практической ценности и расширение сферы применения методов ЛП. Пятидесятые годы явились периодом интенсивного развития данной дисциплины в части разработки новых алгоритмов и теоретических исследований. В настоящее время ЛП с точки зрения уровня теоретических разработок, сферы приложений и реализации вычислительных методов является одним из наиболее развитых направлений в области решения оптимизационных задач. Достижения в области ЛП содействовали прогрессу в разработке алгоритмов решения других задач математического программирования, в том числе в области целочисленного, стохастического и нелинейного программирования. [3]
1 ОБЩЕЕ РЕШЕНИЕ ЗАДАЧИ
1. 1Выбор и обоснование целевой функции
При постановке задачи организационного управления прежде всего важно: 1) определить цель, преследуемую субъектом управления, и 2) установить, значениями каких характеристик (переменных) исследуемой системы (или процесса) можно варьировать.
Под целью будем понимать тот конечный результат, который необходимо получить путем выбора и реализации тех или иных управляющих воздействий на исследуемую систему. В производственно-коммерческой сфере цель, как правило, заключается в том, чтобы либо максимизировать прибыль, либо минимизировать расходы. Цель должна быть представлена в виде функции от управляемых переменных[2] .
Пример.
Пусть имеются i (i=1. . m) сортов взаимозаменяемого сырья в количестве a i , которое используется при производстве j (j=1. . n) продуктов в количестве b j единиц. Матрица C характеризует производственные затраты на единицу продукта (в руб) . Составить оптимальный план посева, если расход сырья (в кг) на единицу продукта (в руб) составляет λ ij .
Обозначим через x lp - количество i- го сорта сырья, используемого при производстве j - го продукта.
Тогда стоимость рассматриваемой единицы продукта оценивается величиной c lp x lp , а общая стоимость всех затрат - величиной ΣΣ c lp x lp .
Таким образом математическая задача формулируется так: найти x 11 , x 12 , . . . , x kr , доставляющие минимум функции
при ограничениях:
Equation. 3
Equation. 3
- Разработка общей математической модели и формулирование задачи оптимизации
Математической моделью называются формальные соотношения, устанавливающие связь принятого критерия эффективности с действующими факторами операции.
Чтобы построить математическую модель, необходимо оценить количественно проявления рассматриваемых факторов и указать группы изменяемых параметров, формально представляющих эти факторы. Однако следует иметь в виду, что никаких правил построения математических моделей не существует. Каждая модель есть проявление знаний, опыта, искусства оперирующей стороны. Процесс создания модели требует четкого осознания цели операции, проникновения в существо моделируемых явлений, умения отделить главное от второстепенного. Математические модели могут иметь вид формул, систем уравнений или неравенств, а также таблиц, числовых последовательностей, геометрических образов, отражающих зависимости между критерием эффективности операции и теми параметрами, которые представляют учтенные действующие факторы[1] .
Пусть математическая модель задачи линейного программирования задана в следующем виде:
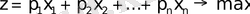 , (1)
, (1)
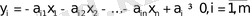 , (2)
, (2)
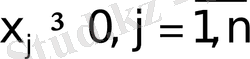 . (3)
. (3)
1. 3 Модифицированные жордановы исключения (МЖИ) .
Основы вычисления схемы симплекс-метода составляют модифицированные жордановы исключения (МЖИ) . Один шаг МЖИ с разрешающим элементом
 переводит исходную таблицу в новую по следующим 5 правилам:
переводит исходную таблицу в новую по следующим 5 правилам:
- Разрешающий элемент заменяется на 1.
- Остальные элементы разрешающей строки остаются без изменения.
- Остальные элементы разрешающего столбца меняют знаки на противоположные.
- Правило четырехугольника:
. (4)
5. Все элементы новой таблицы делятся на разрешающий элемент.
1. 4Алгоритм прямого симплекс-метода.
- Заполнение симплекс-таблицы:
Таблица 1. 1- Исходная симплекс таблица
- Исключение свободных переменных:
Таблица 1. 2- Симплекс таблица, перед исключения свободных переменных
Выписываем выражения для
 :
:
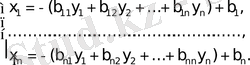 . ( ) (5)
. ( ) (5)
Вычеркиваем их из таблицы 1. 1 . Работу продолжаем в таблице 1. 2.
Таблица 1. 3- Симплекс таблица, после исключения свободных переменных
- Исключение нулевых строк.
Правило выбора разрешающего элемента:
- В качестве разрешающего выбирается столбец, содержащий положительные коэффициенты () .
- Выбор разрешающей строки: вычисляются положительные отношения свободных членов к коэффициентам разрешающего столбца. Среди всех отношений выбирается наименьшее. Таким образом, находится разрешающий элемент. Еще раз выполняется шаг МЖИ.
- Нахождение опорного решения.
- Если все свободные члены таблицы 4 положительные, то опорное решение задается :
y 1 = y 2 = … = y n = 0
y n+1 = b n+1
y m = b m
Значение подставляем в систему и получаем значение х:
х оп = {x 1 оп , x 2 оп , . . . , x n оп }
z оп = Q
- Если некоторые свободные члены отрицательны, то принимаются следующие правила выбора разрешающего элемента:
- Выбирается строка с отрицательным свободным членом (если среди коэффициентов этой строки нет отрицательных, то система несовместима)
- Если среди коэффициентов этой строки есть отрицательные, то выбирается какой-нибудь из них и столбец считается разрешающим
- Вычисляются все неотрицательные отношения, свободных членов к коэффициентам разрешающего столбца. Среди всех отношений выбирается наименьшее . Выполняется шаг МЖИ до тех пор пока не установиться несовместимость систем.
- Нахождение оптимального решения.
Если все коэффициенты z-ой строки положительны, то оптимальное решение найдено.
q 1 ≥0, . . . , q n ≥0; y 1 * = y 2 * = y n * = 0
y n+1 * = b n+1 ; z * = Q; y m * = b m
x * = { x 1 * , x 2 * , . . . , x n * }
Если среди свободных членов есть отрицательные, то применяется следующее правила выбора разрешающего элемента:
- В качестве разрешающего выбирается столбец с отрицательным коэффициентом z-ой строки, если отрицательных коэффициентов несколько, то выбирается наибольший по модулю.
- Отбираются все положительные коэффициенты разрешающего столбца и соответствующие свободные члены делятся на них. Среди всех отношений выбирается наименьшее выполняется шаг МЖИ и так до тех пор пока есть отрицательные коэффициенты z-ой строки, либо не установиться неограниченная z. [3]
1. 5Алгоритм двойственного симплекс-метода.
1) Заполнение симплекс-таблицы (см. 1. 4)
2) Исключение свободных переменных (см. 1. 4)
3) Исключение нулевых строк (см. 1. 4) .
4) Нахождение оптимального решения.
Если все коэффициенты
строки положительны, то 0 является оценкой
сверху и осуществляется переход к шагу 5) . Иначе применяется следующее правило выбора разрешающего элемента:
1Рассматривается столбец с отрицательным коэффициентом z-ой строки.
2 В s-столбце находится некоторый элемент, больший нуля, a rs и строка r считается разрешающей (если все коэффициенты отрицательны, то функция либо неограниченная сверху, либо условия задачи противоречивы) .
3 Вычисляются неположительные отношения коэффициентов z строки к соответствующим коэффициентам разрешающей строки. Среди всех отношений выбирается наибольшее (наименьшее по модулю) . Выполняется шаг МЖИ.
5) Нахождение опорного одновременно оптимального решения.
Если все свободные члены положительны, то опорное одновременно оптимальное решение найдено.
Если среди свободных членов есть отрицательные, то применяется следующее правила выбора разрешающего элемента:
1В качестве разрешающего выбирается строка с отрицательным свободным членом.
2Отбираются все отрицательные коэффициенты этой строки (если среди коэффициентов разрешающей строки нет отрицательных, то условия задачи противоречивы. )
3Вычисляются неположительные отношения коэффициентов z строки к отобранным коэффициентам. Среди всех отношений выбирается наибольшее (наименьшее по модулю) . Выполняется шаг МЖИ. [3]
2 РЕШЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ
2. 1Содержательная формулировка задачи
На металлургическом заводе изготавливается сталь n марок {X 1 , X 2 , …, X n }; сталь изготавливается последовательно в m цехов завода. Производственная мощность каждого из цехов определяется временем обработки одной тонны каждой марки стали и общим временем возможной работы конкретного цеха в определенном периоде. Критерием оптимальности является максимальный общий объём выпуска продукций в денежном выражении:
Z (X) =
. 3
. 3
При ограничениях:
X i
. 3 0,
. 3; вида В
1) Найти оптимальные значения объёма выпуска марок стали X i ,
. 3.
2) Провести моделирование на PC и сравнить полученные результаты с расчетными.
Исходные данные приведены в таблице.
Таблица 1-Данные для решения задачи
Коэффициенты целевой
Функции а i
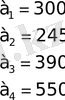
x 1 + 2x 2 + x 3 + 4x 4 ≤ 30; x 1 ≤ 3;
2x 1 + 2x 2 + x 3 + x 4 ≤ 40; 2x 2 ≤ 7;
2x 1 + x 2 + 2x 3 + x 4 ≤ 50; 3x 3 ≤ 18;
x 1 + x 2 + x 3 + 2x 4 ≤ 60; x 4 ≤ 2;
2. 2Построение математической модели
Пусть заданы:
- количество марок стали n;
- количество цехов, в которых последовательно изготавливается сталь m;
- время обработки одной тонны каждой марки стали;
- общее время возможной работы конкретного цеха в определенном периоде.
Необходимо максимизировать общий объем выпуска продукции в денежном выражении:
Z (X) =
. 3
. 3
при ограничениях:
x i
. 3 0,
. 3;
x 1 + 2x 2 + x 3 + 4x 4 ≤ 30;
x 1 ≤ 3;
2x 1 + 2x 2 + x 3 + x 4 ≤ 40;
2x 2 ≤ 7;
2x 1 + x 2 + 2x 3 + x 4 ≤ 50;
3x 3 ≤ 18;
x 1 + x 2 + x 3 + 2x 4 ≤ 60;
x 4 ≤ 2;
2. 3Выбор метода и разработка вычислительного алгоритма решения задачи
Данная задача является задачей линейного программирования, так как целевая функция и ограничения линейного вида и переменные x ij принимают конечные значения из множества значений.
Решение задачи проводится симплексным методом.
2. 3. 1Решение прямым симплекс-методом.
Таблица 2. 1- Исходная симплекс таблица
Таблица 2. 2 - Симплекс таблица (итерация №1)
Таблица 2. 3 - Симплекс таблица (итерация №2)
Таблица 2. 4 - Симплекс таблица (итерация №3)
Таблица 2. 5 - Симплекс таблица (итерация №4)
2. 3. 2Решение двойственным симплекс-методом .
Таблица 2. 6- Исходная симплекс таблица
Таблица 2. 7 - Симплекс таблица (итерация №1)
Таблица 2. 8 - Симплекс таблица (итерация №2)
Таблица 2. 9 - Симплекс таблица (итерация №3)
Таблица 2. 10 - Симплекс таблица (итерация №4)
3 ПРОГРАММНАЯ РАЗРАБОТКА
3. 1 Общие сведения
Программа написана на языке визуального программирования Borland Delphi 7. 0, работающая в основном под Windows.
3. 2 Функциональное назначение
Программа предназначена для нахождения оптимального оптимальные значения объёма выпуска.
... продолжениеПрограммная реализация задачи приведена в ПРИЛОЖЕНИИ А. Листинг программы приведен в ПРИЛОЖЕНИИ В.
3. 3 Описание программного продукта.
- Информатика
- Банковское дело
- Оценка бизнеса
- Бухгалтерское дело
- Валеология
- География
- Геология, Геофизика, Геодезия
- Религия
- Общая история
- Журналистика
- Таможенное дело
- История Казахстана
- Финансы
- Законодательство и Право, Криминалистика
- Маркетинг
- Культурология
- Медицина
- Менеджмент
- Нефть, Газ
- Искуство, музыка
- Педагогика
- Психология
- Страхование
- Налоги
- Политология
- Сертификация, стандартизация
- Социология, Демография
- Статистика
- Туризм
- Физика
- Философия
- Химия
- Делопроизводсто
- Экология, Охрана природы, Природопользование
- Экономика
- Литература
- Биология
- Мясо, молочно, вино-водочные продукты
- Земельный кадастр, Недвижимость
- Математика, Геометрия
- Государственное управление
- Архивное дело
- Полиграфия
- Горное дело
- Языковедение, Филология
- Исторические личности
- Автоматизация, Техника
- Экономическая география
- Международные отношения
- ОБЖ (Основы безопасности жизнедеятельности), Защита труда


