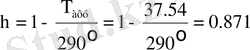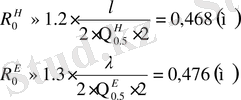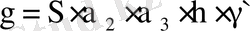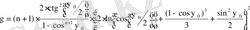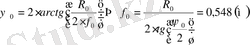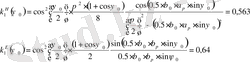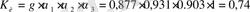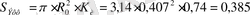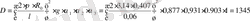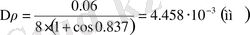Малошумящие однозеркальные параболические антенны: электродинамический и конструктивный расчёт


Тип работы: Реферат
Бесплатно: Антиплагиат
Объем: 13 страниц
В избранное:
РЕСПУБЛИКА КАЗАХСТАН
АЛМАТИТНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
ФАКУЛЬТЕТ РАДИОТЕХНИКИ И СВЯЗИ
Кафедра Радиотехники
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту по дисциплине «Антенно-фидерные устройства и распространение радиоволн»
на тему: “Малошумящие однозеркальные параболические антенны”
Выполнил:
студент группы ССПС-01-2
Дементьев А. И.
№ З. К. 013309
Проверил:
Доцент каф. Радиотехники
Гончаров В. Л.
Алматы 2004
ТЕХНИЧЕСКОЕ ЗАДАНИЕ
Рабочая частота f, ГГц. . . 5, 0
Ширина ДН на уровне половины мощности 2Θ 0, 5 Н , мрад . ……. 77
Ширина ДН на уровне половины мощности 2Θ 0, 5 Е , мрад . …. 82
Уровень боковых лепестков, дБ . . . - 29
Средняя яркостная температура неба Т НСР , ° К . 5
Температура шумов приёмника Т пр , ° К . 1500
Длина фидерной линии l ф , м. . . . . 13
Тип облучателя . . . . Открытый конец прямоугольного волновода
Содержание
Техническое задание 2
Содержание 3
Введение 4
1 Расчет геометрических и электродинамических параметров облучателя и параболоида:
- выбор фидера. Определение шумовой температуры фидерного тракта; 5
- определение диаметра раскрыва; 5
- аппроксимация аналитического вида ДН облучателя функцией вида
cos n/2 Ψ; 6
- определение угла раскрыва и фокусного расстояния зеркальной антенны. 6
2 Расчет геометрических и электродинамических характеристик поля:
- диаграммы направленности облучателя; 8
- распределение поля в апертуре зеркала. 9
3 Расчет пространственной диаграммы направленности и определение параметров параболической антенны. 10
4 Конструктивный расчет антенны:
- расчет профиля зеркала; 12
- выбор конструкции зеркала; 13
- определение допусков на точность изготовления. 14
Выводы 15
Список литературы 17
Приложение А 18
Введение
Параболические антенны в последнее время находят все более широкое применение в космических и радиорелейных линиях связи. В 1888 году известный немецкий физик Г. Герц в своих опытах по СВЧ оптике впервые применил в качестве фокусирующего устройства параболический цилиндр. Интерес к зеркальным антеннам не ослабевает и в наши дни в связи со стремительным развитием космических радиотехнических систем и комплексов. Достаточная простота и легкость конструкции, возможность формирования самых разнообразных диаграмм направленности, высокий КПД, малая шумовая температура - вот основные достоинства, зеркальных антенн, обуславливающих их широкое применение в современных радиосистемах. Целью данной курсовой является освоение методики проектирования зеркальных параболических антенн: определение их основных электродинамических параметров и конструктивный расчет. В курсовой работе определение поля излучения параболической антенны производится апертурным методом, который широко применяем при проектировании зеркальных антенн.
1 Расчет геометрических и электродинамических параметров облучателя и параболоида:
- выбор фидера. Определение шумовой температуры фидерного тракта
В качестве фидера будем использовать прямоугольный волновод для частоты f = 5 ГГц ([1], приложение А) :
a x b = 4. 0 x 2. 0 (см) ;
α = 0. 0431 (дБ/м) .
Шумовая температура фидерного тракта Т афу определяется по формуле:
,
где α - коэффициент затухания линии передачи [дБ/м],
l ф - длина фидерной линии [м] .
КПД определяется по формуле:
- определение диаметра раскрыва
Зеркальная антенна - направленная антенна, содержащая первичный излучатель и отражатель антенны в виде металлической поверхности. Параболическая зеркальная антенна представлена на рисунке 1.
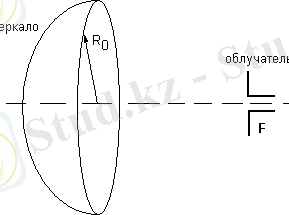
Рисунок 1 - Зеркальная параболическая антенна
В случае равномерно возбуждённого раскрыва параболического зеркала ширина ДН приближённо определяется:
, где
2Θ 0. 5 - ширина диаграммы направленности на уровне половинной мощности, рад. ;
λ - длина волны излучаемого (принимаемого) антенной радиосигнала;
R 0 - радиус раскрыва зеркала (рисунок 1) .
Длина волны определяется по формуле:
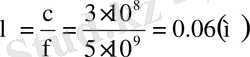
Неравномерное возбуждение раскрыва зеркала приводит к некоторому расширению главного лепестка ДН, так как уменьшается эффективная площадь раскрыва. Чаще всего диаграммы направленности зеркальных антенн не обладают осевой симметрией, т. е. ширина главного лепестка в плоскостях Е и Н различна. В большинстве практических случаев это влечёт за собой следующее изменение:
, где
2Θ Е 0. 5 , 2Θ Н 0. 5 ширина ДН соответственно в плоскостях Е и Н.
Для Е и Н плоскостей соответственно найдем радиус раскрыва:
Т. к. в курсовой имеются данные о ширине диаграммы направленности в обеих плоскостях, можно определить диаметр раскрыва d p = 2 ⋅ R 0 , причем из полученных двух значений диаметра следует выбрать наибольшее. Следовательно, R 0 = 0, 476(м) .
d p = 2 ⋅ R 0 = 2 ⋅ 0, 476 = 0, 952 (м)
- аппроксимация аналитического вида ДН облучателя функцией вида cosn/2Ψ
В зависимости от размещения облучателя относительно зеркала можно получить то или иное значение КНД. При определенном оптимальном отношении R o /f o КНД наибольший. Это объясняется тем, что количество теряемой энергии зависит от формы диаграммы направленности облучателя и от отношения R o /f o . При уменьшении отношения R o /f o от оптимального КНД уменьшается, так как увеличивается часть энергии, проходящей мимо зеркала. С другой стороны, увеличение этого отношения также приводит к уменьшению КНД в связи с более сильным отклонением закона распределения возбуждения от равномерного; оптимальное значение R o /f o определяется по аппроксимированной нормированной ДН облучателя (аппроксимация функцией вида F(θ) =cos n/2 (θ), где n определяет степень вытянутости ДН облучателя) . Для облучателя в виде пирамидального рупора n = 6 ([1], таблица 4. 1) .
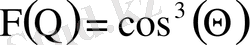
- определение угла раскрыва и фокусного расстояния зеркальной антенны
С точки зрения оптимизации геометрии антенны по максимальному отношению сигнал/шум необходимо произвести следующий расчет.
Чувствительность γ определяется по формуле:
Где первые четыре коэффициента не зависят от ψ о , а γ ' вычисляется:
, где
Т 1 = Т пр + Т 0 ⋅ (1 - η) + η ⋅ Т нср = 1500 ⋅ 290 ⋅ (1 - 0. 871) + 0. 871 ⋅ 5 = 1542 К
Т о = 290 К;
u = (0. 02 - 0. 03) - коэффициент, учитывающий «переливание» части мощности облучателя через края зеркала;
u = 0. 025;
S = π ⋅ R 2 = 3. 14 ⋅ 0, 476 = 0, 712 м 2 , площадь апертуры зеркала;
n = 6 - определяется типом облучателя;
α 1 = 1 - cos n+1 Ψ 0 ;
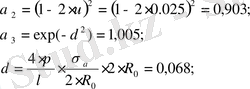
σ а /2R = 0. 4 ⋅ 10 -4 - точность профиля зеркала.
Построим график функции γ`(Ψ 0 ), по максимуму которого определим угол раскрыва зеркала.
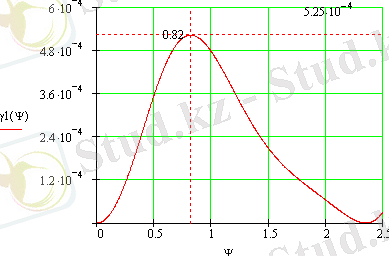
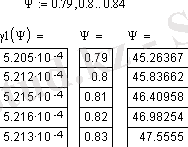
График 1 - График функции γ`(Ψ 0 )
Ψ 0 = 0. 82 (рад) = 46, 983° ⇒ α 1 = 0, 931, g = 0, 877, γ` = 5, 216⋅10 -4 .
Фокусное расстояние f может быть найдено из следующего соотношения:
В зависимости от размещения облучателя относительно зеркала можно получить то или иное значение КНД. При определенном оптимальном отношении R 0 /f 0 КНД наибольший. Заданный интервал отношения R 0 /f 0 = (0. 8÷1. 0) . Расчетное отношение R 0 /f 0 = 0. 89, что удовлетворяет условию.
Определим шумовую температуру антенной системы:
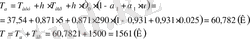
2 Расчет геометрических и электродинамических характеристик поля:
- диаграммы направленности облучателя
Расчет сводиться к определению геометрических размеров облучателя, при которых уменьшение амплитуды поля на краю раскрыва зеркала происходит до одной трети амплитуды поля в центре раскрыва, и диаграммы направленности облучателя.
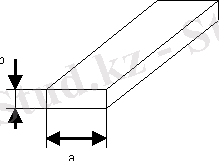
Рисунок 3 - открытый конец прямоугольного волновода
ДН рупорной антенны рассчитываются по формулам:
в Е плоскости
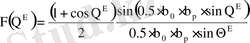
в Н плоскости
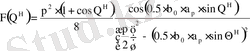 , где
, где
β 0 = 2⋅π/λ - волновое число
 -аппроксимация аналитического вида ДН облучателя
-аппроксимация аналитического вида ДН облучателя
Т. к. Ro-радиус раскрыва зеркала, был вычислен по приблизительной формуле он не удовлетворяет вычислениям, вследствие чего я выбрал Ro=0, 407 (м) удовлетворяющий дальнейшим вычислениям.

d p = 2 ⋅ R 0 = 2 ⋅ 0, 407= 814 (м) ;
S = π ⋅ R 2 = 3. 14 ⋅ 0, 407 = 1, 52 м 2 , площадь апертуры зеркала;
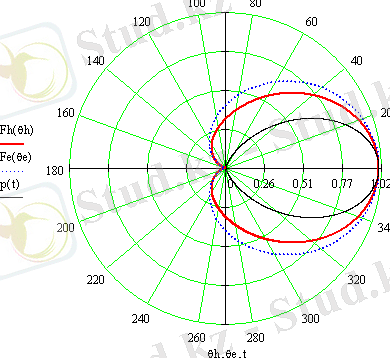
График 2- ДН облучателя (открытый конец прямоугольного волновода)
- распределение поля в апертуре зеркала
Расчет распределения поля в апертуре зеркала осуществляется по следующим формулам:
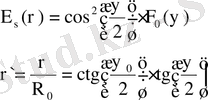 , где
, где
F 0 (Ψ) - диаграмма направленности облучателя, Ψ 0 - угол раскрыва, Ψ - текущий угол.
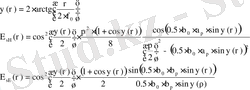 , где
, где
f 0 - фокусное расстояние.
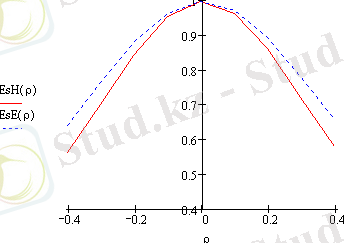
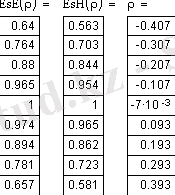
График 3 - Распределение поля в апертуре зеркала
В данном случае Ψ 0 - текущий угол, а Ψ - сдвиг фаз между токами.
3 Расчет пространственной диаграммы направленности и определение параметров параболической антенны
Инженерный расчёт пространственной диаграммы направленности ДН параболической антенны часто сводится к определению ДН идеальной круглой синфазной площадки с неравномерным распределением напряжённости возбуждающего поля. В данном случае распределение напряжённости возбуждающего поля в основном определяется ДН облучателя в соответствующей плоскости. Выражение для нормированной ДН зеркальной параболической антенны при этом имеет вид:
 , где J
1
, J
2
- цилиндрические функции Бесселя первого и второго порядка.
, где J
1
, J
2
- цилиндрические функции Бесселя первого и второго порядка.
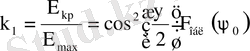 , где
, где
Е кр , Е мах - амплитуды поля на краю и в центре раскрыва.
Коэффициент, показывающий во сколько раз амплитуда возбуждающего поля, на краю раскрыва меньше амплитуды в центре раскрыва в соответствующей плоскости с учётом различий расстояний от облучателя до центра зеркала и до края зеркала;
Построим ДН зеркальной параболической антенны:
- для плоскости Н
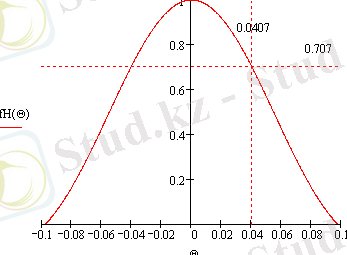
График 4 - Пространственная ДН в плоскости Н
- для плоскости Е
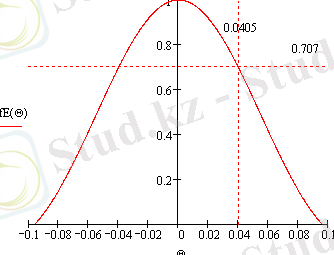
График 5 - Пространственная ДН в плоскости Е
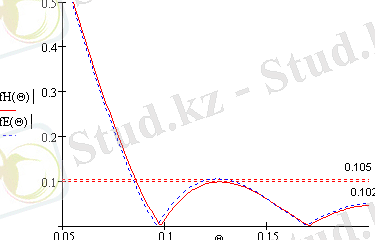
Уровень боковых лепестков.
Для плоскости Е

Для плоскости Н

Приближенно коэффициент направленного действия зеркальной антенны определяется выражением:
, где
S - площадь раскрыва;
υ рез - результирующий коэффициент использования поверхности
Коэффициент использования поверхности:
Эффективная площадь антенны:
Коэффициент направленного действия:
Коэффициент усиления антенны:
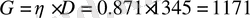
4 Конструктивный расчет антенны
- Расчет профиля зеркала
Зеркальные антенны имеют наибольший КНД при синфазном возбуждении раскрыва (плоский фазовый фронт волны) . Параболический профиль зеркала обеспечивает одинаковые длины электрических путей от облучателя, установленного в фокусе параболоида вращения, до каждой точки плоскости раскрыва (свойство параболы) . В полярной системе координат парабола описывается уравнением
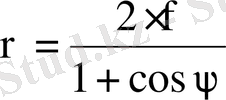 , где
, где
ρ, Ψ - полярные координаты;
f - фокусное расстояние;
Ψ изменяется от 0 до Ψ 0 .
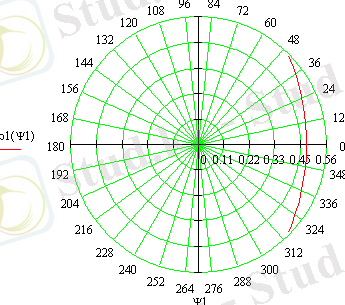
График 6- Плоский фазовый фронт волны
- Выбор конструкции зеркала
С целью уменьшения веса и ветровых нагрузок поверхность зеркала часто выполняется перфорированной, или сетчатой
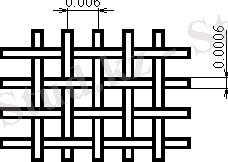
Рисунок 3 - Конструкция зеркала
При такой конструкции зеркала часть энергии просачивается сквозь него, образую нежелательное излучение. Допустимым является значение коэффициента прохождения в обратном направлении.
, где
Р пад , Р обр - мощность излучения падающего на зеркало и в обратном направлении, соответственно.
Двухлинейная сетка работает удовлетворительно при расстоянии между проводниками меньше 0. 1λ и диаметре проводов не менее 0. 01λ.
d п = 0. 1 ⋅ 0. 06 = 0. 006 (м) ;
d = 0. 01 ⋅ 0. 06 = 0. 0006 (м) .
- Определение допусков на точность изготовления
Неточность изготовления зеркала вызывает несинфазность поля в раскрыве. Допустимыми являются фазовые искажения поля в раскрыве зеркала не более ± π/4. При этом уменьшение коэффициента усиления антенны не превышает нескольких процентов.
Пусть поверхность параболоида имеет некоторые неровности (выступы и углубления) . Наибольшее отклонение от идеальной поверхности в направлении ρ обозначим через Δρ.
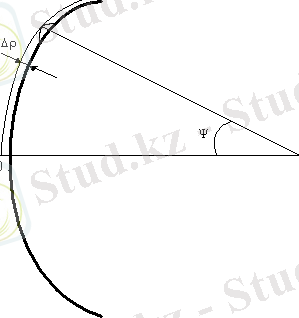
Рисунок 4 - Допуски на точность изготовления зеркала
Путь луча, отраженного от неровности в месте наибольшего отклонения от ρ изменяется при этом на величину ∆ρ + ∆ρ ⋅ cosΨ, а соответствующий сдвиг фаз составит величину ∆ϕ = β⋅∆ρ⋅(1+cosΨ), и он не должен превышать величину π/4, отсюда получаем
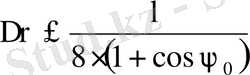
Анализ полученного выражения для ∆ρ показывает, что вблизи центра параболоида (Ψ = 0) необходимая точность изготовления зеркала наивысшая. Здесь наибольшее отклонение от идеальной поверхности не должно превосходить величины λ/16 (т. е. 0. 013) у кромки параболоида требования к точности получаются наименьшими. Точность установки облучателя также определяется нормами на наибольшие допустимые фазовые искажения поля в раскрыве. Пусть фазовый облучатель смещен на ∆х. Тогда длины путей лучей от фазового центра до раскрыва увеличиваются. Наибольшее удлинение пути происходит у лучей, падающих на вершину зеркала. Это удлинение путей при малых смещениях можно приблизительно определить как ∆х⋅cosΨ. Тогда изменение фазы составит величину
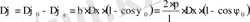 , где
, где
∆ϕ 0 , ∆ϕ а - фазовые искажения , возникающие из-за неточности установки облучателя, в центре и на краю раскрыва, соответственно. Эта величина не должна превышать π/4, отсюда получаем:
Таким образом, с увеличением угла раскрыва точность и установка облучателя в фокусе повышается.
Выводы
В результате проведенной работы сравним полученные данные с исходными:
Исходные данные:
2Θ Н 0. 5 = 77 мрад - ширина ДН на уровне половинной мощности в плоскости Н
2Θ Е 0. 5 = 82 мрад - ширина ДН на уровне половинной мощности в плоскости Е
УБЛ = -29 дБ - уровень боковых лепестков
Рассчитанные данные:
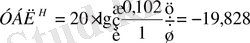 - уровень боковых лепестков в плоскости Н
- уровень боковых лепестков в плоскости Н
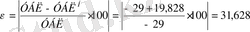 - отклонение боковых лепестков в
- отклонение боковых лепестков в
плоскости Н от заданного значения
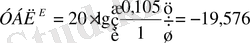 - уровень боковых лепестков в плоскости Е
- уровень боковых лепестков в плоскости Е
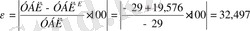 - отклонение боковых лепестков в
- отклонение боковых лепестков в
плоскости Е от заданного значения
Полученная ширина ДН:
2Θ Н 0. 5 = 81, 4 мрад
2Θ Е 0. 5 = 81 мрад
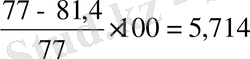 - отклонение в плоскости Н
- отклонение в плоскости Н
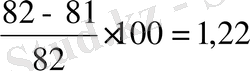 -
отклонение в плоскости Е
-
отклонение в плоскости Е
- Информатика
- Банковское дело
- Оценка бизнеса
- Бухгалтерское дело
- Валеология
- География
- Геология, Геофизика, Геодезия
- Религия
- Общая история
- Журналистика
- Таможенное дело
- История Казахстана
- Финансы
- Законодательство и Право, Криминалистика
- Маркетинг
- Культурология
- Медицина
- Менеджмент
- Нефть, Газ
- Искуство, музыка
- Педагогика
- Психология
- Страхование
- Налоги
- Политология
- Сертификация, стандартизация
- Социология, Демография
- Статистика
- Туризм
- Физика
- Философия
- Химия
- Делопроизводсто
- Экология, Охрана природы, Природопользование
- Экономика
- Литература
- Биология
- Мясо, молочно, вино-водочные продукты
- Земельный кадастр, Недвижимость
- Математика, Геометрия
- Государственное управление
- Архивное дело
- Полиграфия
- Горное дело
- Языковедение, Филология
- Исторические личности
- Автоматизация, Техника
- Экономическая география
- Международные отношения
- ОБЖ (Основы безопасности жизнедеятельности), Защита труда