ТЕОРИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ


МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РЕСПУБЛИКИ КАЗАХСТАН
Казахский национальный технический
университет имени К. И. Сатпаева
Кафедра "Автоматика и телемеханика"
О. И. Ширяева, С. М. Токтабаев
ТЕОРИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Методические указания к выполнению лабораторных работ
в среде MATLAB
(для студентов очного и заочного обучения специальности 050702)
Часть 1
Алматы 2005
УДК 62. 50
СОСТАВИТЕЛИ: Ширяева О. И., Токтабаев С. М. . Теория систем автоматического регулирования. Методические указания к выполнению лабораторных работ в среде MATLAB (для студентов очного и заочного обучения специальности 050702) . Часть 1. Алматы: КазНТУ, 2005. - 36с.
Методические указания составлены в соответствии с требованиями квалификационной характеристики специальности - Автоматизация и управление и предназначены для выполнения лабораторных работ по дисциплине «Теория линейных систем автоматического регулирования». Данные указания содержат краткие сведения из теории автоматического управления, методические примеры выполнения лабораторных работ в среде MATLAB и задания по каждому лабораторному практикуму.
Предназначены для студентов очного и заочного обучения специальности 050702.
Ил. 3. Табл. 1. Библиогр. - 6 назв.
Рецензент: А. А. Бейсембаев, канд. техн. наук., доц.
Печатается по плану издания Министерства образования и науки Республики Казахстан на 2005 г.
КазНТУ, 2005
ВВЕДЕНИЕ
Лабораторные работы направлены на закрепление, систематизацию и расширение полученных знаний по дисциплине «Теория линейных систем автоматического регулирования», а также на овладение практическими навыками при решении конкретных технических задач.
Лабораторный курс разбит на две части:
- первую часть составляют лабораторные работы, связанные с построением математических моделей систем, процессами моделирования, изучением характеристик и преобразованием схем;
- во вторую часть включены лабораторные работы, связанные с решением задач анализа динамических свойств, исследования качества и синтеза систем.
Лабораторные работы, описанные в данном лабораторном практикуме, ориентированы на применение вычислительных машин и программного обеспечения MATLAB, которое в настоящее время является наиболее эффективным средством моделирования систем управления /1/. MATLAB интегрируется с другими прикладными программами, такими как VisSim, Mathcad и т. д. /2/.
Каждая лабораторная работа включает выполнение студентом следующих основных этапов:
- аналитическое решение поставленной задачи путем проработки теоретических положений соответствующего раздела курса и разработки схемы моделирования;
- моделирование задачи с использованием MATLAB;
- объяснение результатов эксперимента с привлечением аналитических методов.
Все экспериментальные методы базируются на предположении о сосредоточенности параметров системы, стационарности во времени ее динамических свойств, линейности систем при малых изменениях входных воздействий и одномерности систем относительно входов и выходов.
Каждую выполненную работу студент должен оформить в виде отчета, который должен содержать:
- цель работы;
- задание;
- полученные результаты по всем пунктам практикума в виде расчетов, схем, команд, таблиц, графиков;
- анализ результатов в соответствии с приведенными теоретическими сведениями;
- выводы по всем пунктам практикума.
В процессе сдачи отчета студент должен ответить на предлагаемые контрольные вопросы и выполнить упражнения по изучаемой теме.
ЛАБОРАТОРНАЯ РАБОТА №1. MATLAB - Основы моделирования
Цель работы: приобретение основных навыков работы с моделирующими программными пакетам MATLAB.
- Основные сведения
MATLAB - система программирования высокого уровня, работающая как интерпретатор и включающая большой набор команд для выполнения самых разнообразных вычислений, задания структур данных и графического представления информации. В частности, используются команды пакета прикладных программ Control System Toolbox, предназначенного для работы с LTI-моделями (Linear Time Invariant Models) систем управления /1/.
MATLAB Simulink - интерактивный инструмент для моделирования, анализа и синтеза динамических систем на основе библиотеки блоков /1, 3/. Simulink является достаточно самостоятельным инструментом MATLAB, но доступ к функциям MATLAB и другим его инструментам остается открытым. Имеются также дополнительные библиотеки блоков для разных областей применения (моделирование электротехнических устройств, набор блоков для разработки цифровых устройств и т. д) .
- Основные принципы работы и моделирования
Лабораторные работы данного практикума выполняются на основе или команд СST или операционных блоков MATLAB Simulink.
Для работы с СST необходимо запустить программу MATLAB и далее работать в командном окне среды MATLAB (рисунок 1. 1), используя набор команд, приведенных в лабораторных работах.
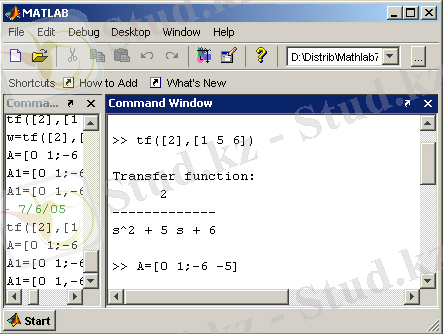
Рисунок 1. 1 - Командное окно MATLAB
Для работы с MATLAB Simulink, после запуска программы MATLAB, необходимо открыть в меню File→New→Model. В открывшемся окне (рисунок 1. 2) собираются модели систем из операционных блоков библиотеки Simulink.
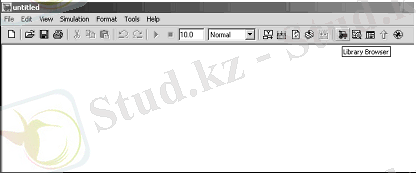
Рисунок 1. 2 - Окно MATLAB Simulink
Окно библиотеки блоков запускается нажатием кнопки Library Browser в меню Simulink и состоит из различных прикладных разделов (рисунок 1. 3)
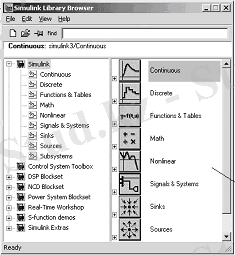
Рисунок 1. 3 - Библиотека MATLAB Simulink
- Методический пример
Моделирование уравнения n -го порядка с начальными условиями с использованием инструментария MATLAB .
Пусть задано дифференциальное уравнение
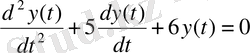 , (1. 1)
, (1. 1)
при начальных условиях (н. у. )
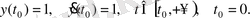
Схема моделирования уравнения (1. 1) в MATLAB Simulink представлена на рисунке 1. 4. Для построения схемы необходимо было разрешить уравнение (1. 1) относительно старшей производной
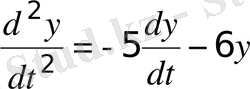 , (1. 2)
, (1. 2)
и воспользоваться в MATLAB Simulink стандартными блоками: сумматор ( Sum ), интегратор ( Integrator ), коэффициент усиления ( gain ), блок вывода характеристик - осциллограф ( Scope ) .
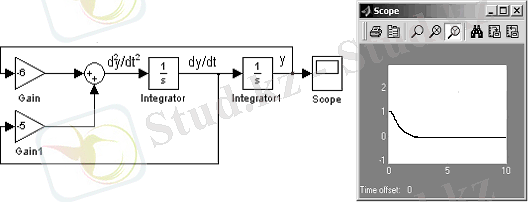
Рисунок 1. 4 - Схема моделирования уравнения (1. 2) в MATLAB Simulink
1. 4 Порядок выполнения лабораторной работы №1
1. Запустить программу MATLAB. Ознакомиться с содержанием меню.
2. Собрать схему рисунка 1. 4, произвольно изменив параметры моделируемых элементов и начальных условий. Записать уравнение модели.
3. Промоделировать дифференциальное уравнение первого и третьего порядков
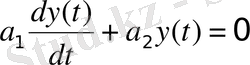 , при н. у.
, при н. у.
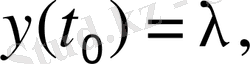
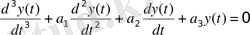 , при н. у.
, при н. у.
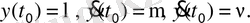
Параметры и начальные условия выбираются самостоятельно или задаются преподавателем.
4. В командном окне
1. 5 Контрольные вопросы
1. Назначение программы MATLAB.
2. Принципы функционирования программных пакетов MATLAB.
3. Возможности моделирования, предоставляемые пакетом прикладных программ Control System Toolbox (СST) и MATLAB Simulink.
4. Основные этапы работы с программой.
ЛАБОРАТОРНАЯ РАБОТА №2. МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ ПРОЦЕССОВ
Цель работы: приобретение навыков построения математических моделей систем автоматического управления, введение основных понятий, терминов и обозначений теории управления.
2. 1 Система автоматического управления. Основные понятия
При создании системы управления технологическим процессом или промышленным объектом необходимо иметь математическое описание объекта управления, управляющего устройства и других элементов, входящих в систему, которые в дальнейшем будем называть звеньями системы автоматического управления (САУ) (рисунок 2. 1) .
Рисунок 2. 1. Структурная схема САУ
Входные переменные, нарушающие равновесие объекта управления, называют возмущающими воздействиями. К ним относится и входной сигнал, используемый для достижения цели управления - управляющее воздействие u ( t ) . В дальнейшем реакцию звена на внешнее воздействие будем обозначать как y ( t ) и называть выходным сигналом .
Математическая модель системы представляет собой совокупность дифференциальных и алгебраических уравнений связи между входными и выходными сигналами.
Алгебраические уравнения описывают установившиеся состояния, когда все производные входных и выходных сигналов равны нулю, и называются уравнениями статики.
Дифференциальные уравнения характеризуют поведение системы во времени при изменении входных воздействий и называются уравнениями динамики.
Для получения динамических характеристик применяют аналитические и экспериментальные методы . Аналитические методы основаны на законах физики, химии, электротехники и др. Часто оказывается эффективным сочетанием аналитических методов с экспериментальными. При этом аналитическим путем находят структуру уравнений связи, а числовые значения коэффициентов уравнений определяют экспериментально.
2. 2 Задача про баки
Целью данной задачи является приобретение практических навыков построения математических моделей процессов, на примере процесса протекающего в баке (рисунок 2. 2) .

Q ( t ) - количество жидкости в баке; q 1 ( t ) - объем втекающей жидкости в единицу времени; q 2 ( t ) - объем вытекающей жидкости в единицу времени; h ( t ) - уровень жидкости в баке; S - площадь днища бака с вертикальными стенками; σ - постоянное проходное сечение.
Рисунок 2. 2 - Схема процесса, протекающего в баке
Алгоритм построения структурной модели динамических процессов:
Шаг 1. Определение основных переменных - причин изменения состояния объекта (входной сигнал), и следствия, которые являются непосредственно наблюдаемым результатом (выходной сигнал) . Для бака:
- входами являются расходы q 1 ( t ) и q 2 ( t ) - две причины изменения уровня жидкости в баке h ( t ) ;
- выходом является уровень h ( t ), который можно непосредственно измерить.
Шаг 2. Определение промежуточных переменных и параметров - какие промежуточные переменные и параметры полезно рассматривать при изучении преобразования первопричин-входов в конечное следствие-выход.
Промежуточные переменные для бака:
∆ q ( t ) - разность расходов;
Q ( t ) - количество жидкости в баке;
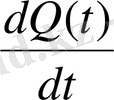 - скорость изменения количества жидкости.
- скорость изменения количества жидкости.
Параметр для бака: площадь днища S .
Шаг 3. Анализ причинно-следственных связей между переменными:
- разность расходов или уравнение баланса расходов имеет вид
∆ q ( t ) = q 1 ( t ) - q 2 ( t ) ; (2. 1)
- разность расходов определяет скорость изменения количества жидкости
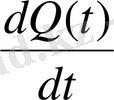 =∆
q
(
t
), (2. 2)
=∆
q
(
t
), (2. 2)
- количество жидкости
Q
(
t
) в каждый момент времени
t
>0 определяется его начальным значением
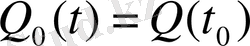 и накоплением за время
t
>0:
и накоплением за время
t
>0:
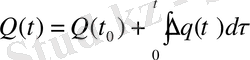 , (2. 3)
, (2. 3)
- зависимость уровня h ( t ) от объема Q ( t ) как
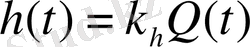 , (2. 4)
, (2. 4)
где k h - постоянный коэффициент.
Шаг 4. Построение структурной схемы.
Зависимости (2. 1-2. 4) можно описать структурной схемой , которая представляет собой совокупность блоков-преобразователей и связей между ними (рисунок 2. 3) .
Рисунок 2. 3 - Структурная схема объекта
Преобразователь 1 - сумматор или элемент сравнения, отражает зависимость баланса расходов от входов и соответствует уравнению (2. 1) . Зачерненный сектор отмечает переменную, входящую в алгебраическую сумму со знаком ''минус".
Преобразователь 2 описывает зависимость количества жидкости Q ( t ) от скорости его изменения по уравнению (2. 3) .
Преобразователь 3 - зависимость уровня жидкости h ( t ) от ее количества Q ( t ) по уравнению (2. 4) .
Аналитическая математическая модель процесса заполнения или опорожнения бака описывается в виде дифференциального уравнения
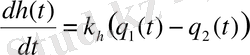 Equation. 3,
Equation. 3,
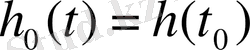 ,
,
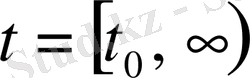 , (2. 5)
, (2. 5)
где t - непрерывное время;
t 0 - начальное время;
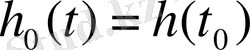 - начальное условие.
- начальное условие.
Приведем подробный процесс получения уравнения (2. 5) . Разрешим уравнение (2. 4) относительно величины Q ( t )
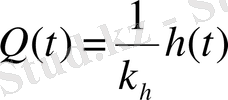 ,
,
и продифференцируем правую и левую части полученного выражения
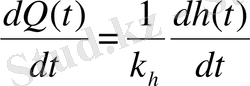 . (2. 6)
. (2. 6)
В соответствии с выражением (2. 2), уравнение (2. 6) приведем к виду
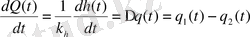 =>
=>
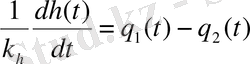 . (2. 7)
. (2. 7)
Умножив правую и левую части уравнения (2. 7) на коэффициент k h получим выражение (2. 5) .
С учетом с обозначением входных и выходных сигналов через u ( t ) и y ( t ), математическую модель бака (2. 5) можно представить в виде в абстрактном виде
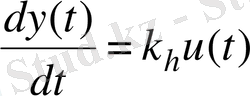 Equation. 3,
Equation. 3,
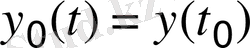 ,
,
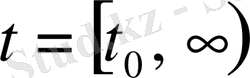 .
.
2. 3 Временные характеристики
Для аналитического получения характеристики выходного сигнала y ( t ), в теории автоматического управления выделяют два типовых входных воздействия во временной области: единичная ступенчатая функция и импульсное воздействие /4, 5/.
Переходной характеристикой h ( t ) называется реакция звена (системы) на единичное ступенчатое воздействие u ( t ) =1( t ) при нулевых начальных условиях.
Единичная ступенчатая функция (рисунок 2. 4) представляет собой мгновенное изменение величины воздействия с нуля до единицы
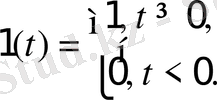
Рисунок 2. 4 - Единичный ступенчатый сигнал.
Для автоматических систем 1( t ) является распространенным видом входного воздействия. Как правило, подобные воздействия сопровождают процессы включения систем и вызывают переходы от одного установившегося состояния к другому.
Весовая характеристика это реакция звена (системы) на импульс u ( t ) =δ( t ), который можно рассматривать как дельта-функцию Дирака
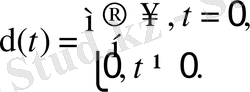
Для автоматических систем импульсное воздействие является менее распространенным видом входного воздействия, чем единичная ступенчатая функция. Однако для теоретического описания систем имеет существенное значение. Подобные воздействия характерны для радарных комплексов - описывают передачу импульса при упругом взаимодействии или для гидродинамических систем - моделируют гидравлические удары, возникающие при включении или выключении насосов.
2. 3 Методический пример
Для моделирования переходного процесса в MATLAB Simulink используется блок подачи на вход объекта ступенчатого сигнала - Step .
Например, схема получения переходного процесса объекта управления, математическая модель которого имеет вид
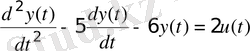 ,
,
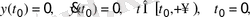 (2. 12)
(2. 12)
представлена на рисунке 2. 5.
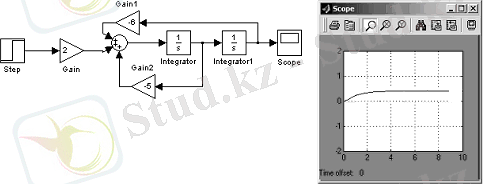
Рисунок 2. 5 - Моделирование переходного процесса (2. 12)
2. 4 Порядок выполнения лабораторной работы №2
1. Построить математической модель и структурную схему бака.
2. Построить схемы моделирования в среде MATLAB Simulink.
3. Выбрать параметры динамических процессов и при их варьировании получить значения снимаемых сигналов в различных точках схемы.
4. Снять переходные и весовые характеристики объекта управления.
2. 5 Контрольные вопросы
1. Объект управления, управляющее устройство, САУ.
2. Математическая модель объекта управления.
3. Уравнения статики и уравнения динамики.
5. Входные воздействия и выходные координаты объекта управления. Возмущающее воздействие, управляющее воздействие.
6. Структурная схема САУ. Основные элементы структурных схем.
7. Алгоритм построения структурной модели динамических процессов.
8. Переходная характеристика, весовая характеристика.
ЛАБОРАТОРНАЯ РАБОТА №3. ФОРМЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ СИСТЕМ УПРАВЛЕНИЯ
Цель лабораторной работы: приобретение навыков в работе с различными формами представления математических моделей систем автоматического управления.
3. 1 Основные теоретические сведения
Существуют следующие формы представления математических моделей систем управления /6/:
- дифференциальное уравнениеn-го порядка
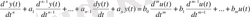 , (3. 1)
, (3. 1)
где t - непрерывное время;
t 0 - начальное время;
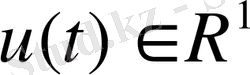 -
управляющее воздействие;
-
управляющее воздействие;
y ( t ) - выходной сигнал;
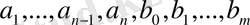 - постоянные коэффициенты, определяемые физическими параметрами звена (системы) ;
- постоянные коэффициенты, определяемые физическими параметрами звена (системы) ;
n
- порядок дифференциального уравнения системы,
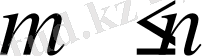 .
.
- передаточная функция - отношение преобразования по Лапласу выходной величины к преобразованию по Лапласу входной величины при нулевых начальных условиях
, (3. 2)
где s - оператор Лапласа;
y ( s ) и u ( s ) - изображения y ( t ) и u ( t ), соответственно.
Знаменатель выражения (3. 2) определяет характеристический полином
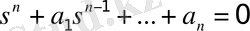 , (3. 3)
, (3. 3)
решениями которого являются корни
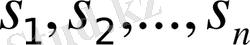 .
(3. 4)
.
(3. 4)
Корни (3. 4) называются полюсами передаточной функции. Корни числителя передаточной функции называются нулями передаточной функции.
Представление систем в виде передаточной функции имеет в основном технические преимущества: исследователь имеет дело с физическими переменными не только в конечном результате, но и на промежуточных этапах, и зачастую имеет возможность сопровождать теоретическое исследование экспериментом. Но при таком представлении математические описания различных систем и блоков даже в линейном случае получаются разнотипными в зависимости от порядков числителей и знаменателей их передаточных функций.
3) системой дифференциальных уравнений в пространстве состояний , которое дает более единообразное и удобное математическое описание.
Для этого вводят вместо выходных переменных
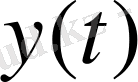 переменные состояния
переменные состояния
 . Описание системы в этих переменных дается системой дифференциальных уравнений первого порядка
. Описание системы в этих переменных дается системой дифференциальных уравнений первого порядка
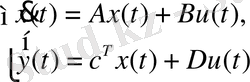 . 3
. 3
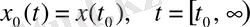 , (3. 5)
, (3. 5)
где
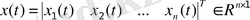 -
вектор переменных состояний объекта управления;
-
вектор переменных состояний объекта управления;
 ,
,
 ,
,
 ,
,
 - матрицы состояния, управления, наблюдаемости (матрица выхода по состоянию), выхода по управлению соответственно.
- матрицы состояния, управления, наблюдаемости (матрица выхода по состоянию), выхода по управлению соответственно.
Переход к уравнениям в переменных состояния неоднозначен: выполняя различные преобразования, для одной и той же системы можно получать различные формы /1/. В данном лабораторном практикуме рассмотрим переход только к нормальной форме .
Если в (3. 1) m =0, то уравнение (3. 1) n -го порядка можно привести к системе из n дифференциальных уравнений первого порядка
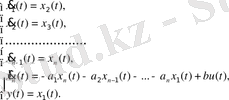 (3. 6)
(3. 6)
Матричную форму системы (3. 6) можно получить, введя в рассмотрение вектор
 и матрицы
и матрицы
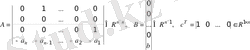 .
.
Если в (3. 1) m ≤ n , то нормальная форма имеет вид
 (3. 7)
(3. 7)
где
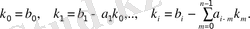 Equation. 3
Equation. 3
3. 2 Методический пример
Получим переходной процесс для системы (2. 12), передаточная функция и пространство состояний которой имеют вид
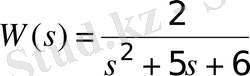 ,
,
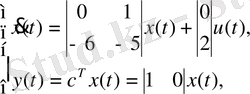 (3. 8)
(3. 8)
1 способ (MATLAB Simulink) . Использование блоков Transfer Function (передаточная функция) (рисунок 3. 1) и State Space (пространство состояний) (рисунок 3. 2) .
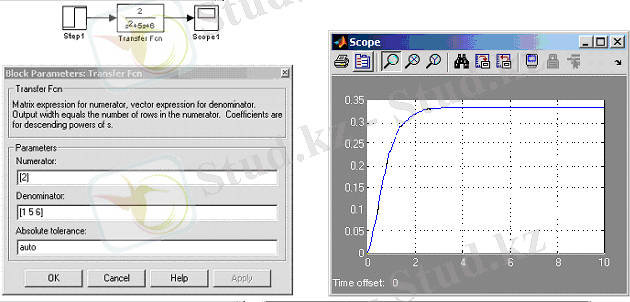 а) схема моделирования; б) блок задания параметров; в) переходной процесс
а) схема моделирования; б) блок задания параметров; в) переходной процесс
Рисунок 3. 1 -Использование блока Transfer Function
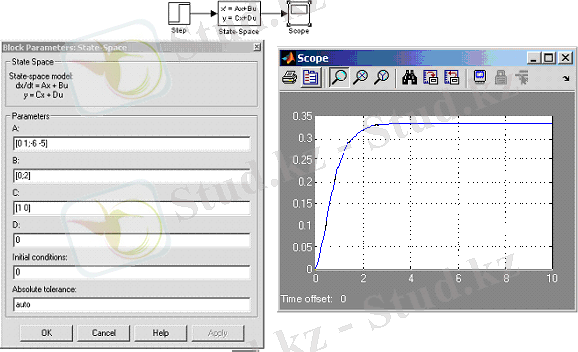
а) схема моделирования; б) блок задания параметров; в) переходной процесс
Рисунок 3. 2 - Использование блока State Space в MATLAB
2 способ (в командном режиме среды MATLAB с использованием команд CST) . В CST имеется тип данных, определяющих систему как LTI-модель в виде передаточной функции или пространства состояний, а также команды для построения характеристик (таблица 3. 1)
Таблица 3. 1 - Команды CST
Представление LTI-модели в виде передаточной функции,
где b m , …, b 1 - значения коэффициентов числителя передаточной функции;
a n , …, a 1 - значения коэффициентов характеристического полинома.
Определение нулей передаточной функции
Определение полюсов передаточной функции
В командном окне MATLAB создадим LTI-объект (3. 8) с именем w и получим переходную характеристику (рисунок 3. 3)
>>w=tf([2], [1 5 6] )
>> step(w)
В командном режиме MATLAB создадим LTI-объект (3. 8) с именем s и получим переходную характеристику (рисунок 3. 3)
>> A=[0 1; -6 -5]
>> B=[0; 2]
>> c=[1 0]
>> s=ss(A, B, c, 0)
>> step(w)
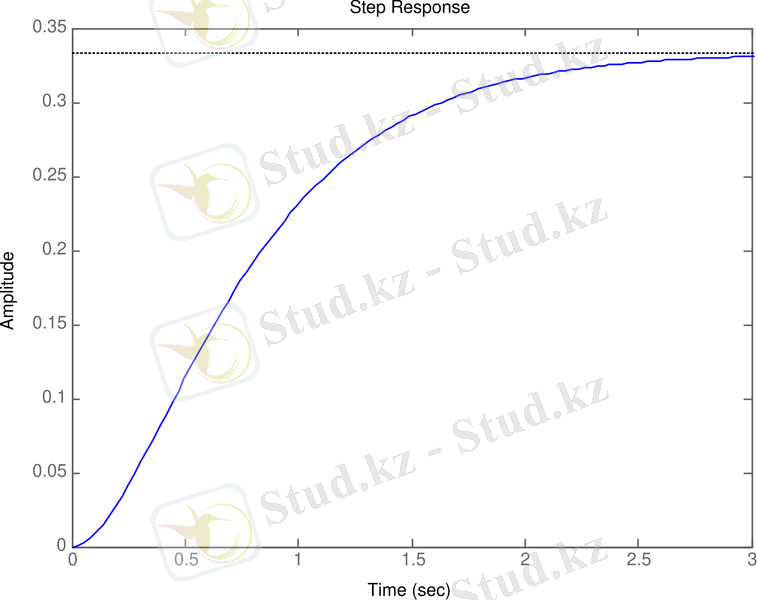
Рисунок 3. 3 - Переходной процесс, полученный с использованием CST
По рисункам 3. 1., 3. 2 и 3. 3 можно отметить идентичность переходных процессов, полученных по различным формам представления математической модели системы управления.
3. 3 Порядок выполнения лабораторной работы №3
1. Для объекта, математическая модель которого описывается уравнением n -го порядка (таблица 3. 1), получить передаточную функцию и математическую модель в пространстве состояний.
Таблица 3. 1 - Исходные данные
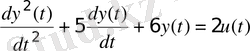
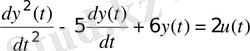
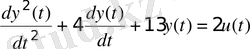
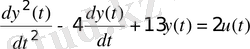
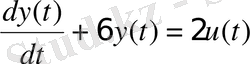
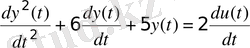
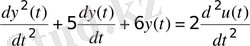
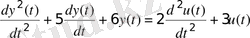
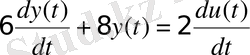
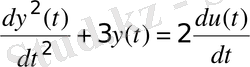
2. Используя команды пакета CST или MATLAB Simulink получить переходные процессы объекта, описываемого передаточной функцией и математической моделью в пространстве состояний. Сравнить полученные результаты.
3. Определить нули и полюса передаточной функции.
3. 4 Контрольные вопросы
1. Формы представления математических моделей систем автоматического управления.
2. Передаточная функция.
3. Характеристическое уравнение.
4. Нули и полюса передаточной функции.
5. Математическая модель САУ в пространстве состояний. Нормальная форма в пространстве состояний.
6. Преимущества каждой из форм математического описания систем управления.
ЛАБОРАТОРНАЯ РАБОТА №4. ИССЛЕДОВАНИЕ Переходных ХАРАКТЕРИСТИК ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ
Цель работы: экспериментальное исследование взаимосвязей между параметрами типовых динамических звеньев и их характеристиками. Приобретение навыков работы с типовыми звеньями систем.
4. 1 Типовые звенья САУ
Различные системы автоматического регулирования при расчете обычно разбиваются на динамические звенья. Под динамическим звеном понимают устройство любого физического вида и конструктивного оформления (механические, электрические и т. д. ), описываемое определенным дифференциальным уравнением. В соответствии с этим классификация звеньев проводится именно по виду дифференциального уравнения /7, 8/.
Сложные динамические звенья удобно разделить на простейшие составные части - типовые динамические звенья , передаточные функции которых имеют в числителе и знаменателе полиномы от s не выше второго порядка.
В таблице 4. 1 приведены наиболее распространенные типовые звенья, их дифференциальные уравнения и передаточные функции. Передаточную функцию динамического звена в общем случае можно представить как произведение сомножителей следующего вида
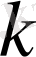 ;
s
v
;
;
s
v
;
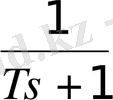 Equation. 3 ;
Equation. 3 ;
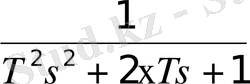 Equation. 3 ;
Equation. 3 ;
 Equation. 3
Equation. 3
 Equation. 3
Equation. 3
где k > 0 - коэффициент усиления или передачи звена ;
v может быть и отрицательным целым числом;
T > 0 - постоянная времени ( сек. ) ;
0
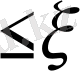 <1 - степень затухания;
<1 - степень затухания;
τ> 0 - время запаздывания.
Наличие нулей или полюсов передаточных функций типовых звеньев - это признак для разбиения последних на три группы: позиционные, интегрирующие и дифференцирующие. По таблице 4. 1:
... продолжение- Информатика
- Банковское дело
- Оценка бизнеса
- Бухгалтерское дело
- Валеология
- География
- Геология, Геофизика, Геодезия
- Религия
- Общая история
- Журналистика
- Таможенное дело
- История Казахстана
- Финансы
- Законодательство и Право, Криминалистика
- Маркетинг
- Культурология
- Медицина
- Менеджмент
- Нефть, Газ
- Искуство, музыка
- Педагогика
- Психология
- Страхование
- Налоги
- Политология
- Сертификация, стандартизация
- Социология, Демография
- Статистика
- Туризм
- Физика
- Философия
- Химия
- Делопроизводсто
- Экология, Охрана природы, Природопользование
- Экономика
- Литература
- Биология
- Мясо, молочно, вино-водочные продукты
- Земельный кадастр, Недвижимость
- Математика, Геометрия
- Государственное управление
- Архивное дело
- Полиграфия
- Горное дело
- Языковедение, Филология
- Исторические личности
- Автоматизация, Техника
- Экономическая география
- Международные отношения
- ОБЖ (Основы безопасности жизнедеятельности), Защита труда