Анализ и синтез линейных систем автоматического регулирования по заданным показателям качества

Тип работы: Реферат
Бесплатно: Антиплагиат
Объем: 11 страниц
В избранное:

МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РЕСПУБЛИКИ КАЗАХСТАН

Казахский национальный технический университет

имени Каныша Сатпаева

Кафедра электропривод и автоматизация технологических комплексов

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К КУРСОВОМУ ПРОЕКТУ

Тема: Анализ и синтез линейных систем автоматического регулирования по заданным показателям качества.

Руководитель:

должность, уч. степень и звание

Т. С. Малдыбаева И. О. Ф.

« ___» 2003 г.

Нормоконтролёр:

А. О. Бердибеков И. О. Ф.

«___» 2003 г.

Студент:

Копбаев Е. Ф. И. О.

Специальность: 3308

Группа: АЭП-00-1

Алматы 2003

МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РЕСПУБЛИКИ КАЗАХСТАН

Казахский национальный технический университет

имени Каныша Сатпаева

Институт автоматики и управления

Специальность электропривод и автоматизация технологических комплексов

Кафедра электропривод и автоматизация технологических комплексов

УТВЕРЖДАЮ

Зав. кафедрой

И. О. Ф.

« » 2003 г.

ЗАДАНИЕ

НА ВЫПОЛНЕНИЕ КУРСОВОГО ПРОЕКТА

Студенту Копбаев Е Ф. И. О.

Тема проекта. Анализ и синтез линейных систем автоматического регулирования по заданным показателям качества.

Утверждена приказом по вузу № от « »

Срок сдачи законченного проекта

Исходные данные к проекту

\[K_{\nu}=5.29,T_{1}=0.12,T_{2}=0.1,T_{\nu}=0.02,T_{\alpha}\ =0.08,E_{\partial d}=0.6,\ \ =2.09_{\alpha},{\bf D}=449t_{\nu},t_{\rho}=1.6c,\mu=2.\]

критерий устойчивости Гурвица и Михайлова.

Содержание расчетно-пояснительной записки:

Введение

1 Составление структурной схемы исходной системы.

2 Оценка устойчивости исходной САР по критериям устойчивости.

3 Построение переходного процесса САР при ступенчатом возмущении на входе с использованием операторного метода.

4 Определение показателей качества исходной системы.

5 Выбора метода улучшения динамических свойств исследуемой системы.

6 Построение ЛАЧХ исходной системы и корректирующего устройства.

7 Составление структурной схемы скорректированной САР и определение её передаточной функции

8 Расчет и построение переходного процесса скорректированной САР по вещественным частотным характеристикам.

Заключение.

Перечень графического материала:

Схема системы СМУ-ДПТ

Структурная схема исходной САР

Годограф

Переходный процесс

Построение ЛАЧХ

Построение ВЧХ

Разбиение ВЧХ на типовые трапеции, вписывающимися в основной контур ВЧХ и прилежащим к оси ординат

Структурная схема скорректированной САР

Построение переходного процесса

Дата выдачи задания 19. 03. 03

Заведующий кафедрой М. А. Нурлыбаев

Руководитель проекта: Малдыбаева. Т. С

Задание принял к исполнению студент: Абдыкалыков. Г. Е

Дата « »

ВВЕДЕНИЕ

В данной работе произведен динамический расчет типовой системы электропривода, выполненного по схеме силовой магнитный усилитель- двигатель постоянного тока с независимой обмоткой возбуждения (СМУ-ДПТ), которая приведена на рисунке 1(лист1) .

Данная работа состоит из разделов.

Первый раздел посвящается анализу исходной системы и включает в себя следующие подразделы:

составление структурной схемы исходной системы;
оценка устойчивости исходной САР по критериям устойчивости;
построение переходного процесса САР при ступенчатом возмущении на входе с использованием операторного метода и определение показателей качества исходной системы.

Второй раздел посвящён синтезу САР, отвечающий требуемым показателям качества регулирования и включает в себя следующие подразделы:

- обоснование выбора метода улучшения динамических свойств исследуемой системы;

- построение ЛАЧХ исходной системы;

- обоснование формы, расчет и построение ЛАЧХ желаемой системы;

- построение ЛАЧХ корректирующего устройства и определение его передаточной функции;

- составление структурной схемы скорректированной САР и определение её передаточной функции;

- получение аналитического выражения для ВЧХ скорректированной САР, расчет и построение ВЧХ;

- разбиение ВЧХ на типовые трапеции, вписывающимися в основной контур ВЧХ и прилежащим к оси ординат, определение параметров трапеций;

- нахождение с помощью таблиц h-функций для каждой трапеции, характеризуемой определенным значением коэффициента наклона, нормированного переходного процесса и расчет нормированных процессов в натуральный масштаб;

- графическое построение составляющих переходного процесса, получение общего результирующего процесса и определение качества скорректированной системы.

1 АНАЛИЗ ИСХОДНОЙ САР

1 Составление структурной схемы исходной системы

В данной работе СМУ и ДПТ аппроксимированы инерционными звеньями второго порядка, а ТГ-безинерционным звеном. Структурная схема исходной системы дана на рисунке2 (лист2) .

2 Оценка устойчивости исходной САР

Определив структурную схему исходной системы необходимо произвести оценку устойчивости по критерию Гурвица и критерию Михайлова [3 стр. 185-189] .

Прежде чем использовать эти критерии необходимо определить характеристическое уравнение исходной системы. Для этого, используя правила преобразования структурных схем [1стр. 9] необходимо получить передаточную функцию замкнутой исходной системы и получить её операторное выражение в виде

\[W(p)={\frac{b_{0}\,p^{m}+b_{1}p^{m-1}+\ldots+b_{m}}{a_{0}\,p^{n}+a_{1}\,p^{n-1}+\ldots+a_{n}}}\]

(1)

Передаточная функция исходной системы имеет вид:

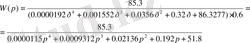(2)

Прировняв знаменатель передаточной функции к нулю, получим характеристическое уравнение.

\[H(p)=0.0000115p^{4}+0.0009312p^{3}+0.02136p^{2}+0.192p+51.8=0\]

(3)

все коэффициенты характеристического уравнения положительны, т. е. необходимое условие выполняется. Составим таблицу - схему Гурвица

0. 0009312: 0. 0009312

0. 192: 0. 192

0: 0

0. 0009312: 0. 115

0. 192: 0. 02136

0: 51. 8

0: 0

0. 0009312: 0

0. 192: 0. 0009312

0: 0. 192

0: 0

0. 0009312: 0

0. 192: 0. 115

0: 0. 02136

0: 51. 8

Система неустойчива, т. к. согласно критерию Гурвица для устойчивости системы необходимо и достаточно, чтобы

\[{\hat{a}}_{4}>0\]

все коэффициенты были положительны.

Принимаем

\[\begin{array}{l}{a_{0}=0.0000115}\\ {a_{1}=0.0009312}\\ {a_{2}=0.02136}\\ {a_{3}=0.192}\\ {a_{4}=51.8}\end{array}\]

Для четвертого порядка достаточно

\[\hat{a}_{3}(\hat{a}_{1}\times\hat{a}_{2}\ -\ \hat{a}_{0}\times\hat{a}_{3})-\ \hat{a}_{1}^{2}\cdot\hat{a}_{4}\geq0\]

\[0.192(0.0009312\times0.02136<0.0000115\times0.02)\cdot0.0009312^{2}\times1.8=-0.0000037\]

Исследуем систему на устойчивость, используя критерий Михайлова.

Вновь записываем характеристическое уравнение

\[H(p)=0.0000115p^{4}+0.0009312p^{3}+0.02136p^{2}+0.192p+51.8=0\]

Производим замену

\[p\to\ j\omega\]

и переписываем уравнение

\[\begin{array}{l}{{H(p)=0.000115(j w)^{4}+0.0009312(j w)^{3}+0.02136(j w)^{2}+0.192(j w)+51.8=\qquad\qquad}}\\ {{=(0.000115w^{4}<0.0.02136w^{2}+51.8)+(-0.0009312w^{2}+0.192\omega)}}\end{array}\]

Выделяем мнимую и вещественную часть, строим годограф.

\[\begin{array}{l c r}{{P(w)=0.000115w^{4}-0.02136w^{2}+51.8}}\\ {{Q(w)=0.192w-0.0009312\omega^{3}}}\end{array}\]

Таблица 1-Расчетные данные для построения годографа

\[{\boldsymbol{C}}\]

0: 0

2: 2

4: 4

6: 6

8: 8

10: 10

15: 15

20: 20

25: 25

30: 30

\[{\cal P}(_{(U)})\]

0: 36. 38

2: 34. 23

4: 27. 86

6: 12. 4

8: -0. 53

10: -7. 184

15: -9. 244

20: -11. 83

25: -3. 84

30:

\[Q(\omega)\]

0: 0

2: -1. 019

4: -19. 024

6: -26. 21

8: -23

10: -16

15: -9. 9

20: -2. 21

25: -1. 09

30:

Система неустойчива, так как годограф рисунок 3 не охватывает точку (-1; 0) .

3 Операторный метод построения переходного процесса САР

Для построения переходного процесса воспользуемся второй теоремой разложения Карсона-Хевисайда [3стр. 216] .

\[Y(t)={\frac{F_{1}(0)}{F_{2}(0)}}+\sum_{K=1}^{n}{\frac{F_{1}(P_{k})}{P_{k}\times F_{2}^{\prime}(P_{k})}}\cdot e^{p_{K}x}\]

(5)

Для построения переходного процесса операторным методом необходимо:

1 Определить передаточную функцию системы и привести её к виду (1) ;

2 Найти производную знаменателя выражения (1) ;

3 Вычислить корни выражения (3) ;

4 Вычислить выражение (5) при подстановке в него всех корней характеристического уравнения и при изменении
\[\frac{x{\mathcal{A}}}{\beta\quad\ }\]
от нуля до
\[\infty\]
.

\[W(p)=\frac{85.3}{0.000115p^{4}+0.0009312p^{3}+0.02136p^{2}+0.192p+51.8}\]

(6)

Подготовка

\[F_{1}(0)=85.3\]

\[F_{2}(p)=0.0000115p^{4}+0.0009312p^{3}+0.02136p^{2}+0.192\,\vec{\vartheta}+51.8\]

\[\begin{array}{c}{{F_{1}(0)=85.3}}\\ {{F_{2}(0)=51.8}}\\ {{F_{\frac{1}{2}}(0)}}\\ {{F_{\underline{{{1}}}}(0)=1.7}}\end{array}\]

\[F_{2}^{\,^{\prime}}(p)=0.000046p^{3}+0.0027936p^{2}+0.04272\,p+0.192\]

Для этого необходимо определить корни характеристического уравнения с использованием метода итераций [2 стр. 59-61] . Прировняв знаменатель передаточной функции к нулю, получим характеристическое уравнение.

\[H(p)=0.0000115p^{4}+0.0009312p^{3}+0.02136p^{2}+0.192p+51.8=0\]

Корни полученных уравнений

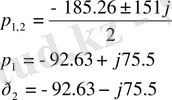
\[\begin{array}{c}{{p_{3,4}=\frac{\displaystyle b\pm\sqrt{D}}{\displaystyle b_{3}=41.8+j67}=\frac{83.6\pm134\,j}{\displaystyle2}}}\\ {{\displaystyle\frac{\displaystyle\bar{Y}}{\displaystyle\partial_{4}=41.8-j67}\qquad\qquad\qquad\qquad\qquad}}\end{array}\]

Вычисляем

\[F_{2}^{\,^{\cdot}}(p)=0.0000288\,p^{3}+0.0022\,p^{\,2}+0.472\,p+0.273\,\]

Подставляя полученные корни в выражение (5), Произведя все необходимые преобразования получим:

\[Y(t)=2.48+\hat{a}^{-98.83n}\left[0.012\sin75.5t-0.025t\right]+\hat{a}^{41.3t}\left[0.174\sin67t-0.15\cos67t\right]\]

(6)

Далее, подставляя в выражение (6) различные значения t, можно построить переходной процесс рисунок 4.

Таблица 2- Расчетные данные для построения переходного процесса

T: T

0: 0

0. 05: 0. 05

0. 08: 0. 08

0. 12: 0. 12

0. 18: 0. 18

0. 2: 0. 2

0. 25: 0. 25

T: Y(t)

0: 2. 305

0. 05: 3. 375

0. 08: -4. 015

0. 12: 32. 45

0. 18: -396. 7

0. 2: 122. 1

0. 25: -2573. 4

4 Определение прямых показателей качества регулирования

\[\sigma\,=\,\infty\]

\[t_{\partial}=\ \infty\]

\[{\boldsymbol{\mu}}=\infty\]

\[\scriptstyle{0=\cdots}\]

Сравниваем с заданными

\[\displaystyle\hat{t}_{\partial}\ --\hat{t}_{\cdot}\hat{\mathrm{O/}}\]

\[\mu=2\]

\[\mathrm{D}=47_{\mathcal{O}}\]

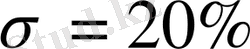
Определив показатели качества и сравнив их с заданными, видно, что система неработоспособна так как прямые показатели качества регулирования системы не равны заданным и следовательно необходимо скорректировать систему таким образом, чтобы прямые показатели качества системы удовлетворяли заданным.

5 Выбор способа улучшения динамических свойств системы

Из всех предлагаемых способов коррекции системы наиболее простой способ последовательного синтеза. Способ коррекции с помощью последовательного корректирующего устройства не требует сложных расчетов и наиболее прост в практическом исполнении, поэтому этот способ рекомендуется для использования в данной работе. При использовании последовательного корректирующего устройства

\[W_{K}(\ p)\]

передаточная функция скорректированной САР системы равна

\[W_{\alpha}\left(p\right)=W_{K}\left(p\right)\cdot W_{\dot{\alpha}\bar{\alpha}}(p)\]

(7)

Из формулы (7) имеем

\[W_{\tilde{E}}\left(p\right)=W_{\alpha}\left(p\right)/W_{\tilde{e}\tilde{m}}(p)\]

(8)

тогда логарифмические частотные характеристики последовательного корректирующего устройства определяются выражениями

\[\begin{array}{c}{{{\cal L}_{\scriptscriptstyle K}={\cal L}_{\scriptscriptstyle\bar{K}}\,-\,{\cal L}_{\bar{E}\bar{Q}}\,-\,{\bar{\cal E}}\bar{\cal A}\times\bar{O}}}\\ {{\ {\scriptstyle j}_{\scriptscriptstyle\dot{K}}\,=j\,{\,}_{\scriptscriptstyle\dot{K}}\,-\,\phi_{\scriptscriptstyle\dot{B}\bar{Q}}\,-\bar{\cal E}\bar{O}\times\bar{O}}}\end{array}\]

(9)

Для выбора последовательного корректирующего устройства достаточно иметь лишь логарифмическую частотную характеристику [1стр. 14-16] .

6 Построение ЛАЧХ системы

Строим ЛАЧХ для разомкнутой системы. Записываем передаточную функцию для разомкнутой системы

\[W(p)=\frac{85.3}{0.000115p^{4}+0.0009312p^{3}+0.02136p^{2}+0.192p+51.8}\]

(10)

Строим ЛАЧХ исходной системы рисунок 5

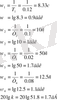
Строим желаемую ЛАЧХ

Для построения желаемой ЛАЧХ, нам необходимы прямые показатели качества регулирования (исходные данные) и эмпирическая формула Салодовникова. А также, с помощью графика кривых Салодовникова [1стр. 19] нужно определить частоту положительности

\[K=85.3;\]

\[t_{p}={\frac{m p}{\omega_{\mathrm{r}}}}\]

\[\ t_{p}\ -\vert_{*}\Theta\widetilde{n}\]

\[s\ =20\bar{\varphi}_{v}=>w_{i}=\frac{3.2\pi}{1.6}=6.28\]

\[\begin{array}{c}{{w_{\bar{n}\bar{o}}=0.8_{\bar{t}}\ \mathrm{w}_{\bar{t}}=5.024}}\\ {{w_{\bar{o}}=1g.024=0.7\bar{d}\hat{e}}}\end{array}\]

Строим ЛАЧХ корректирующего устройства

\[{\cal L}_{\scriptscriptstyle K}\,=\,{\cal L}_{\scriptscriptstyle\scriptscriptstyle\scriptscriptstyle K}\,-\,{\cal L}_{\scriptscriptstyle\hat{E}\hat{N}\hat{D}}\,-\,\bar{E}\hat{A}\times\cal O\]

\[\begin{array}{l}{{K^{\prime}\colon20\lg K^{\prime}=-\ 23.4}}\\ {{\mid\mathbf{g}K^{\prime}={\frac{-}{20}}=-1.17}}\\ {{K^{\prime}=10^{-1.7}=0.07}}\end{array}\]

\[\begin{array}{l}{{T^{*}\dot{\cal T}^{*}=\frac{1}{w^{*}}=\frac{1}{1.17}=0.85\dot{n}}}\\ {{T^{**}\dot{\cal T}^{**}=\frac{1}{w^{*+}}=\frac{1}{10}=0.12\tilde{n}}}\\ {{T^{***}\dot{\cal T}^{***}=\frac{1}{2.02}=\frac{1}{3.0}=0.03\tilde{n}}}\end{array}\]

Передаточная функция корректирующего устройства имеет вид

\[W_{e i o}\left(p\right)=\frac{20(1+0.1\partial)(1+0.08\,\partial)(1+0.02)}{(1+0.12\,\partial)}\,;\]

Составление структурной схемы САР и определение её передаточной функции

Строим структурную схему системы с корректирующим звеном рисунок 6, а передаточная функция системы будет иметь вид

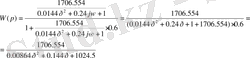(11)

8 Построение переходного процесса методом трапеций

Для построения переходного процесса методом трапеций необходимо получить аналитическое выражение для ВЧХ скорректированной САР и определить её передаточную функцию. Для этого в выражении (11) производим замену

\[p\to\ j\omega\]

и в полученном выражении выделяем вещественную часть

\[W(j w)=\frac{1706.554}{0.00864j w^{2}+0.144j\omega+1024.5}\]

избавившись в знаменателе от комплексного числа, передаточная функция приобретает вид

\[W(j w)=\frac{\mid706.554}{(0.00864w^{2}+0.144w w+1024.5}\]

\[P(w)=\frac{14.74w^{2}+1748364.6}{0.00074649w^{4}-0.020736\omega^{2}+1049600.3}\]

Таблица 3-Расчетные данные для построения ВЧХ

\[{\mathcal{O}}\]

0: 0

0. 5: 0. 5

1: 1

2: 2

3: 3

5: 5

8: 8

10: 10

12: 12

\[P(\omega)\]

0: 1. 688

0. 5: 1. 652

1: 1. 57

2: 1. 29

3: 0. 98

5: 0. 53

8: 0. 19

10: 0. 09

12: 0. 02

ВЧХ представлена на рисунке 7.

Далее разбиваем ВЧХ на трапеции рисунок 8 (лист 8) и находим основные параметры трапеций. Затем, используя таблицы h-функций [1стр. 19] для каждой трапеции строим свой собственный переходной процесс, с помощью формул

\[t=t_{\partial\bar{\alpha}\bar{e}}\;^{\prime}\;d\omega_{0i}\]

\[{\cal X}(t)=P_{0i}\cdot h_{i}(t_{\partial\bar{d}\bar{d}e}\;/\omega_{0i})\]

\[g=stackrel{W_{d i}}{\mathcal{J}}_{\omega_{o i}}\]

Затем графически строим составляющие переходного процесса и получаем общий результирующий процесс рисунок 9.

Таблица 4-Пересчет нормированных процессов в натуральный масштаб

... продолжение

Вы можете абсолютно на бесплатной основе полностью просмотреть эту работу через наше приложение.