Пояснительная записка к курсовому проекту: разработка игры Кости на Delphi с применением теории игр и VCL


Тип работы: Курсовая работа
Бесплатно: Антиплагиат
Объем: 32 страниц
В избранное:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Казахский национальный технический университет имени К. И. Сатпаева
Кафедра технической кибернетики
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту
тема Разработка развлекательной программы
Старший преподаватель
Б. Б. Тусупова
«___»2005г.
СтудентБихасимова А. А.
Специальность 370140, КСОИиУ
Группа КСУ-02-2к
Алматы 2005
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. .
1 ЗАДАНИЕ. .
2 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ . . .
2. 1 Теория игр . . .
2. 1. 1 Оптимальные решения в играх двух лиц с нулевой суммой……… . . .
2. 1. 2 Пример. .
2. 1. 3 Смешанные стратегии.
2. 1. 4 Решение игр вида (mxn) с помощью линейного программирования.
2. 2 Среда DELPHI…. .
2. 2. 1 Библиотека визуальных компонентов VCL и ее базовые классы……
2. 2. 2 Иерархия базовых классов.
2. 2. 3 Класс Tobject
2. 2. 4 Класс Tcontrol. .
2. 2. 5 Страницы палитры компонентов . . …
3 ПРАКТИЧЕСКАЯ ЧАСТЬ . . .
3. 1 Обобщенный алгоритм. .
3. 2 Разработка пользовательского интерфейса. . ……. .
3. 3 Функциональное назначение. … . . .
3. 4 Логическая структура программы
3. 5 Вызов и загрузка
3. 6 Требуемые технические средства.
3. 7 Входные данные
3. 8 Выходные данные.
3. 9 Описание контрольного примера ЗАКЛЮЧЕНИЕ . . . СПИСОК ЛИТЕРАТУРЫ. …… . . .
Приложение . . . . .
1 ЗАДАНИЕ
Разработать программу, моделирующую игру “Кости”. Играющий называет любое число в диапазоне от 2 до 12 и ставку, которую он делает в этот ход. Программа с помощью датчика случайных чисел дважды выбирает числа от 1 до 6 (“бросает кубик”, на гранях которого цифры от 1 до 6) Если сумма выпавших цифр меньше 7 и играющий задумал число меньше 7, он выигрывает сделанную ставку. Если сумма выпавших цифр больше 7, он также выигрывает сделанную ставку. Если играющий угадал сумму цифр, он получает в четыре раза больше очков, чем сделанная ставка. Ставка проиграна, если не имеет место ни одна из описанных ситуаций. В начальный момент у играющего 100 очков. В программе должно присутствовать графическое изображение поверхности кубика при каждом ходе игрока.
2 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
2. 1 Теория игр
В теории игр противников принято называть игроками. Каждый игрок имеет некоторое множество (конечное или бесконечное) возможных выборов, называемых стратегиями. Результаты ли платежи в игре задаются функциями, зависящими от стратегий каждого игроков. Игры с двумя игроками, в которых выигрыш одного равен проигрышу другого, известны как игры двух лиц с нулевой суммой. В такой игре достаточно задать результаты в виде платежей для одного из игроков.
2. 1. 1 Оптимальные решения в играх двух лиц с нулевой суммой
Обычно выбор критерия в задачах принятия решений в значительной мере определяется имеющейся информацией. Игры представляют собой предельный случай полного отсутствия информации, когда разумные противник находятся в состоянии конфликта. В силу этого для решения игры двух лиц нулевой суммой обычно предлагается очень «пессимистичный» критерий, так называемый критерий минимакса- максимина.
Чтобы учесть. Что каждый из игроков действует против другого, критерий минимакса выделяет из всех стратегий (чистых или смешанных) те, которые дают наилучшие или наихудшие возможные результаты. Говорят, что оптимальное решение достигнута, если ни одному из игроков невыгодно изменить свою стратегию. В этом случае игра считается стабильным или находящейся в состоянии равновесия.
Так как обычно матрица игры представляет выигрыш игрока А (стратегии которого определяются строками), критерий предписывает игроку А выбрать такую стратегию (чистую или смешанную), которая максимизирует его минимальный выигрыш, причем минимум берется по всем стратегиям игрока В. Точно так же игрок В выбирает стратегию, которая минимизирует его максимальный проигрыш. Максимум теперь берется по стратегиям игрока А.
Следующий пример показывает, каким образом подсчитываются минимаксное и максиминное значение игры.
2. 1. 2 Пример
Рассмотрим следующую платежную матрицу, которая определяет выигрыши игрока А. Вычислим минимаксное и максиминное значения в заданной игре
Игрок В
1 2 3 4 Минимумы
в строках
1 8 2 9 5 2
Игрок А 2 6 5 7 18 5 Максимин
3 7 3 -4 10 -4
Максимумы 8 5 9 18
В столбцах Минимакс
Если игрок А выбирает первую стратегию, он может получить 8, 2, 9, или 5 в зависимости от стратегии, выбранной игроком В. Его выигрыш будет не меньше min{8, 2, 9, 5}=2 независимо от поведения игрока В. Аналогично при выборе игроком А второй стратегии гарантированный выигрыш будет равен min{6, 5, 7, 18}=5, и, наконец, если он выбирает третью стратегию, гарантированный выигрыш будет равен min{7, 3, -4, 10}=-4. Таким образом, минимальные значения в каждой строке определяют минимально гарантированный выигрыш для игрока А, если он выбирает соответствующую стратегию. Эти значения указаны в столбце «Минимумы в строках». Теперь игрок А, выбирая вторую стратегию, максимизирует свой минимальный выигрыш. Его значение равно max{2, 5, -4}=5. Выбранная игроком А стратегия называется максиминной стратегией, а соответствующее ей значение выигрыша-максиминным (нижним) значением игры.
Игрок В хочет минимизировать свой проигрыш. Выбрав первую стратегию, он может проиграть не более чем max{8, 6, 7}=8 независимо от выбора своего противника. Подобные рассуждения можно продолжить для остальных трех стратегий. Соответствующие результаты указаны выше в строке «Максимумы в столбцах». Игрок В выбирает стратегию, которая минимизирует его максимальные проигрыши. Такой стратегией будет вторая, для которой проигрыш игрока В составит min{8, 5, 9, 18}=5. Это стратегия называется минимаксной, а соответсвующее ей значение проигрыша игрока В- минимаксным (или верхним) значением игры.
Из условий, определяющих критерий минимакса, следует, что минимаксное (верхнее) значение всегда больше, чем максиминное (нижнее) значение, или равно ему. В случае когда имеет место равенство, т. е. минимаксное значение равно максиминному, соответствующие чистые стратегии называются оптимальными, а про игру говорят, что она имеет седловую точку. Значение игры, определяемое парой оптимальных чистых стратегий, равно минимаксному и максиминному значениям. «Оптимальность» здесь означает, что ни один игрок не стремится изменить свою стратегию, так как его противник может на это ответить выбором другой стратегии, дающей худший для первого игрока результат. Вообще значение игры должно удовлетворять неравенствам:
Максиминное (нижнее) значение
 Значение игры
Значение игры
 Минимаксное (верхнее) значение.
Минимаксное (верхнее) значение.
В вышеприведенном примере максиминное значение равно минимаксному значению (=5) . Это означает, что игра имеет седловую точку, задаваемую элементом матрицы. Значение игры, таким образом, равно 5. Отметим, что ни один из игроков не может улучшить свою позицию выбором какой-нибудь другой стратегии.
2. 1. 3 Смешанные стратегии
В предыдущем подразделе показано, что из существования седловой точки непосредственно следует существование оптимальных чистых стратегий в игре. Однако некоторые игры могут не иметь седловых точек. Рассмотрим, например, следующую игру с нулевой суммой:
Игрок В
1 2 3 4 Минимумы
в строках
1 5 -10 9 0 -10
Игрок А 2 6 7 8 1 1
3 8 7 15 2 2 Максимин
4 3 4 -1 4 -1
Максимумы 8 7 15 4
В столбцах Минимакс
Минимаксное знпчение (равное 4) больше, чем максиминное (равное 2) . Следовательно, данная игра не имеет седловой точки и максиминно-минимаксные стратегии неоптимальны. Это приводит к тому, что каждый из игроков может улучшить свое положение, выбрав другую стратегию. В таком случае говорят, что игра нестабильна (неравновесна) .
Поскольку, пользуюсь чистыми максиминно-минимаксными стртегиями, в общем случае невозможно получить оптимальные решения игры, появилась идея использования смешанных стратегий. Каждый игрок вместо выбора одной из чистых стратегий может выбирать любую из них с заранее заданными вероятностями. Пусть
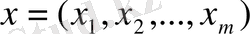 и
и
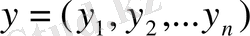 - наборы вероятностей, с которыми игроки А и В соответственно выбирают свои чистые стратегии. Тогда
- наборы вероятностей, с которыми игроки А и В соответственно выбирают свои чистые стратегии. Тогда
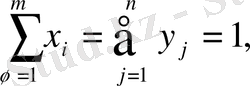
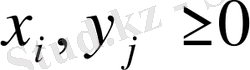 для всех
для всех
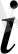 и
и
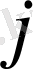 . Если
. Если
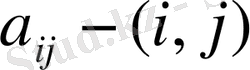 -й элемент матрицы игры, то платежная матрица будет иметь следующий вид:
-й элемент матрицы игры, то платежная матрица будет иметь следующий вид:
В

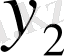
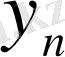
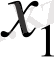
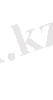
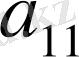
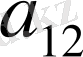
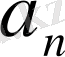
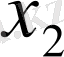
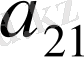
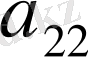
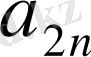
.
.
.
.
.
.
.
.
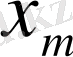
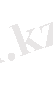
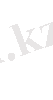
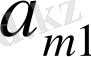
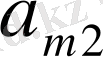
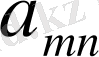
А
Подход к определению решения игры при смешанных стратегиях также основывается на критерии минимакса, введенном в подразд. 2. 1. 1. Единственная разница заключается в том, что игрок А выбирает
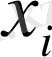 так, чтобы максимизировать наименьшей ожидаемый выигрыш по столбцам, тогда как игрок В выбирает
так, чтобы максимизировать наименьшей ожидаемый выигрыш по столбцам, тогда как игрок В выбирает
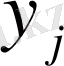 с целью минимизировать наибольшей ожидаемый проигрыш по строкам. Математически критерий минимакса при смешанных стратегиях может быть описан следующим образом. Игрок А выбирает стратегию
с целью минимизировать наибольшей ожидаемый проигрыш по строкам. Математически критерий минимакса при смешанных стратегиях может быть описан следующим образом. Игрок А выбирает стратегию
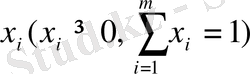 , дающую
, дающую
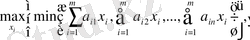
а игрок В выбирает стратегию
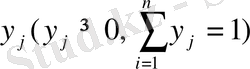 , дающую
, дающую
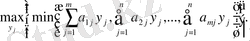
Эти величины определяются соответственно как ожидаемые максиминные и минимаксные платежи.
Как и в случае чистых стратегий, выполняется соотношение
Минимаксный ожидаемый проигрыш
 Максиминный ожидаемый выигрыш.
Максиминный ожидаемый выигрыш.
Когда
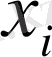 и
и
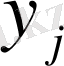 соответствует оптимальным решениям, выполняется строгое равенство, и результирующее значение равно ожидаемому (оптимальному) значению игры. Это утверждение следует из теоремы о минимаксе и приведено здесь без доказательства. Если
соответствует оптимальным решениям, выполняется строгое равенство, и результирующее значение равно ожидаемому (оптимальному) значению игры. Это утверждение следует из теоремы о минимаксе и приведено здесь без доказательства. Если
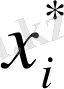 и
и
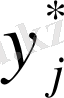 - оптимальные решения для обоих игроков, каждому элементу платежной матрицы
- оптимальные решения для обоих игроков, каждому элементу платежной матрицы
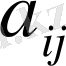 соответствует вероятность
соответствует вероятность
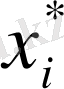
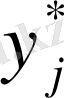 . Следовательно, оптимальное ожидаемое значение игры
. Следовательно, оптимальное ожидаемое значение игры
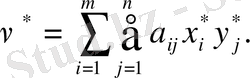
Известно несколько методов нахождения оптимальных стратегий
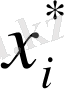 и
и
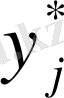 в играх двух лиц с нулевой суммой.
в играх двух лиц с нулевой суммой.
2. 1. 4 Решение игр вида (mxn) с помощью линейного программирования
Теория игр находится в тесной связи с линейным программированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования и, наоборот, каждая задача линейного программирования может быть представлена как игра Г. Данцинг указывает, что создатель теории игр Дж. фон Нейман, который первым ввел симплекс-метод в линейное программирование устоновил что соотношение и в дальнейшем обосновал и развил концепцию двойственности в линейном программировании. В этом разделе описывается способ нахождения решения игры методам линейного программирования, который особенно эффективен для игр, описываемых матрицей большой размерности.
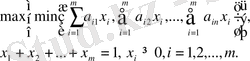
Эта задача может быть сформулирована в виде задачи линейного программирования. Пусть
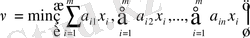
Тогда задача принимает вид:
максимизировать
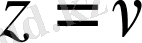
при ограничениях
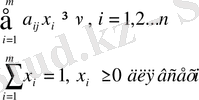
где
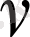 является значением игры.
является значением игры.
Полученная задача линейного программирования может быть упрощена делением всех n+1 ограничением на
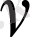 . Это операция возможно при
. Это операция возможно при
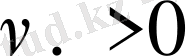 . В противном случае если
. В противном случае если
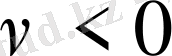 необходимо изменить знаки неравенств. При
необходимо изменить знаки неравенств. При
 деление, естественно, недопустимо. Но этот случай не представляет особых затруднений, так как можно прибавить положительное число К ко всем элементам платежной матрицы, что гарантирует положительность значения модифицированной игры. Тогда истинное значение игры может быть получено вычитанием К из модифицированного значения. Вообще, если максминное значение игры неотрицательно, значение игры больше нуля (при условии, что игра не имеет седловой точки) .
деление, естественно, недопустимо. Но этот случай не представляет особых затруднений, так как можно прибавить положительное число К ко всем элементам платежной матрицы, что гарантирует положительность значения модифицированной игры. Тогда истинное значение игры может быть получено вычитанием К из модифицированного значения. Вообще, если максминное значение игры неотрицательно, значение игры больше нуля (при условии, что игра не имеет седловой точки) .
Таким образом, предполагая
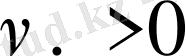 , ограничения задачи могут быть записаны в виде
, ограничения задачи могут быть записаны в виде
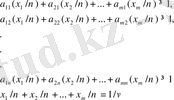
Положим
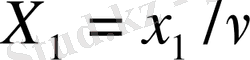 для i=1, …, m. в силу того что
для i=1, …, m. в силу того что
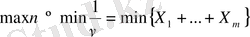 ,
,
задача принимает вид
минимизировать
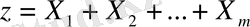
при ограничениях
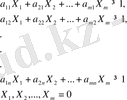
Для игрока В задача записывается в виде
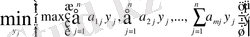
при ограничениях
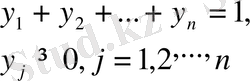
Эта задача также может быть записана как задача линейного программирования:
максимизировать
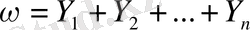
при ограничениях
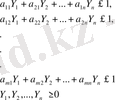
где
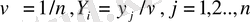
 Equation. 3 Отметим, что задача игрока В является двойственной к задаче игрока А. Тем самым оптимальное решение одной из задач автоматически дает оптимальное решение другой задачи. Задача игрока В может быть решена, например, стандартным симплекс-методом, а игрока А- двойственным симплекс-методом. Выбор метода определяется тем, какая из задач имеет меньше ограничений, что в свою очередь завить от числа чистых стратегий каждого из игроков.
Equation. 3 Отметим, что задача игрока В является двойственной к задаче игрока А. Тем самым оптимальное решение одной из задач автоматически дает оптимальное решение другой задачи. Задача игрока В может быть решена, например, стандартным симплекс-методом, а игрока А- двойственным симплекс-методом. Выбор метода определяется тем, какая из задач имеет меньше ограничений, что в свою очередь завить от числа чистых стратегий каждого из игроков.
2. 2 Среда DELPHI
Прикладные программы, или приложения Delphi создаются в интегрированной среде разработки (IDE-Integrated Development Environment) . Пользовательский интерфейс служит для организации взаимодействия с программистом и включает в себе ряд окон, содержащих различные элементы управления. С помощью средств интегрированной среды разработчику удобно проектировать интерфейсный часть приложения, а также писать программный код и связать его с элементами управления. В интегрированный среде разработки проходят все этапы создания приложения, включая отладку. [1]
Интегрированная среде разработки Delphi представляет собой многооконную систему. Вид интегрированной среды разработки (пользовательский интерфейс ) может различаться в зависимости от настроек. После загрузки интерфейс Delphi выглядит так, как показано на рис. 1. 1 и первоначально включает шесть окон:
главное окно (Delphi-Project1) ;
окно Обоззревателя дерево объектов (Object Tree View) ;
окно Инспектора объектов (Object Inspector) ;
окно Формы, или конструктора формы (Form1) ;
окно редактора кода (Unit1) ;
окно Проводника кода (Exploring Unit1. pas) .
Последние два окно находится позади окна Формы, причем окно Проводника кода пристыковано слева к окну Редактора кода, поэтому обо этих окна имеет общий заголовок Unit1. pas. [1]
На экране кроме указанных окон могут присутствовать и другие окна, отображаемые при вызове соответствующих средств, например, окно Редактора изображений (Image Editor) . Окно Delphi можно перемещать, изменять их размер и убрать с экрана (кроме главного окна), а также состыковать между собой. [1]
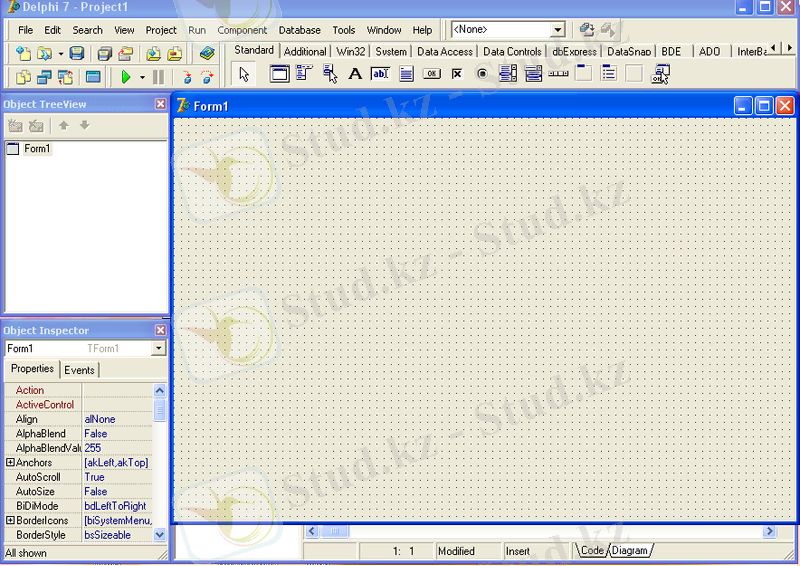 Рисунок 2. 1 - Вид интегрированной среды разработки.
Рисунок 2. 1 - Вид интегрированной среды разработки.
2. 2. 1 Библиотека визуальных компонентов VCL и ее базовые классы
Все классы библиотеки визуальных компонентов произошли от группы базовых классов, которые лежат в основе иерархии VCL. Самый общий предок компонентов - это класс TObject, инкапсулирующий простейший объект. Как известно (см. гл. 1), каждый объект наследует свойства и методы родительского класса. К объекту можно добавить новые свойства и методы, но нельзя удалить унаследованные. Объект-наследник в свою очередь может стать родительским для нового класса, который унаследует возможности всех своих предков. [2]
Поэтому иерархия базовых классов VCL продумана чрезвычайно тщательно - ведь на их основе создано все множество компонентов, используемых в Delphi. Особое место среди базовых классов, помимо TObject, занимают TComponent (от него происходят все компоненты) и TControl (от него происходят все элементы управления) . [2]
В этой главе рассматривается иерархия базовых классов и их возможности. Представленные здесь сведения помогут разобраться с основными механизмами функционирования компонентов. Настоящая глава послужит справочным материалом для тех, кто создает собственные объекты и элементы управления. [2]
2. 2. 2 Иерархия базовых классов
В основе всего многообразия классов и компонентов, используемых в Delphi, лежат всего лишь пять базовых классов (риснок 1. 2) . Они обеспечивают выполнение основных функций любого объекта - будь это стандартный компонент VCL или специализированный объект, выполняющий некоторые операции в приложении. [3]
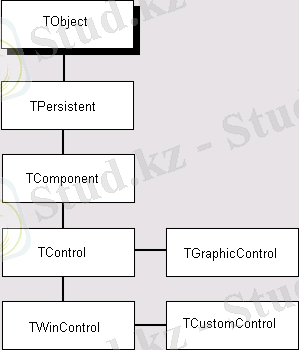
Рисунок 2. 2 - Иерархия базовых классов VCL
Благодаря механизму наследования свойств и методов, потомки базовых классов умеют "общаться" друг с другом; работают в среде разработки, взаимодействуя с Палитрой компонентов и Инспектором объектов; распознаются операционной системой как элементы управления и окна. [3]
В основе иерархии классов лежит класс TObject. Он обеспечивает выполнение важнейших функций "жизнедеятельности" любого объекта. Благодаря ему, каждый класс получает в наследство механизмы создания экземпляра объекта и его уничтожения. [3]
Обычно разработчик даже не задумывается о том, как объект будет создан и что необходимо сделать для его корректного уничтожения. Компоненты VCL создаются и освобождают занимаемые ресурсы автоматически. Иногда разработчику приходится создавать и удалять объекты самостоятельно. Но даже в этом случае ему достаточно вызвать соответствующие конструктор и деструктор:
var SomeList: TStrings;
. . .
SomeList := TStrings. Create;
. . .
SomeList. Free;
За кажущейся простотой этих операций скрывается довольно сложная реализация указанных процессов. Практически весь исходный код класса TObject написан на ассемблере для обеспечения наибольшей эффективности операций, которые будут выполняться в каждом его потомке. [3]
Кроме этого, класс TObject обеспечивает создание и хранение информации об экземпляре объекта и обслуживание очереди сообщений.
Класс TPersistent происходит непосредственно от класса TObject. Он обеспечивает своих потомков возможностью взаимодействовать с другими объектами и процессами на уровне данных. Его методы позволяют передавать данные в потоки, а также обеспечивают взаимодействие объекта с Инспектором объектов. [3]
Класс TComponent является важнейшим для всех компонентов. Непосредственно от него можно создавать любые невизуальные компоненты. Механизмы, реализованные в классе TComponent, обеспечивают взаимодействие компонента со средой разработки, главным образом с Палитрой компонентов и Инспектором объектов. Благодаря возможностям этого класса, компоненты начинают работать на форме проекта уже на этапе разработки. [3]
Класс TControl происходит от класса TComponent. Его основное назначение - обеспечить функционирование визуальных компонентов. Каждый визуальный компонент, произошедший от TControl, наделяется основными признаками элемента управления. Благодаря этому, каждый визуальный компонент умеет работать с GUI (Graphic User Interface - графический интерфейс пользователя ОС) и отображать себя на экране. [3]
Класс TWinControl расширяет возможности разработчиков по созданию элементов управления. Он наследуется от класса TControl и обеспечивает создание оконных элементов управления. [3]
На основе класса TWinControl создан еще один дополнительный класс - TCustomControl. Он обеспечивает создаваемые на его основе компоненты возможностями по использованию канвы - специального объекта, предназначенного для отображения графики (подробнее о канве см. гл. Л) . [3]
Класс TCustomControl является общим предком для целой группы классов, обеспечивающих создание различных нестандартных типов оконных (получающих фокус) элементов управления Windows: редакторов, списков и т. д. [3]
Для создания неоконных (не получающих фокус) элементов управления используется класс TGraphicControl, являющийся потомком класса TControli.
В целом иерархия базовых классов обеспечивает полноценную работу разработчиков в Delphi, позволяя проектировать любые типы приложений. [3]
Ниже мы остановимся на основных свойствах и методах базовых классов, выделяя только те, которые могут пригодиться в реальной работе. Часть из них доступна в Инспекторе объектов, часть может быть использована в программном коде. [3]
2. 2. 3 Класс TObject
Класс TObject является родоначальником всей иерархии использующихся в Delphi классов VCL. Он реализует функции, которые обязательно будет выполнять любой объект, который может быть создан в среде разработки. Учитывая гигантское разнообразие возможных областей применения объектов в процессе создания приложений, можно сказать, что круг общих для всех классов операций весьма невелик. [1]
В первую очередь - это создание экземпляра объекта и его уничтожение. Любой объект выполняет эти две операции в обязательном порядке. Процесс создания объекта включает выделение области адресного пространства, установку указателя на экземпляр объекта, задание начальных значений свойств и выполнение установочных действий, связанных с назначением объекта. В общем случае две последние операции могут не выполняться. [1]
Указатель на экземпляр объекта передается в переменную объектного типа, которая в дальнейшем будет идентифицировать объект в программном коде приложения. В приведенном выше фрагменте кода переменная объектного типа someList объявлена как экземпляр типа TStrings. При создании экземпляра этого типа конструктор Create возвращает в переменную SomeList указатель на выделенную для нового объекта область памяти. Для этого применяется метод Newinstance, который вызывается в конструкторе автоматически:
class function Newinstance: TObject; virtual;
Объект класса TObject обеспечивает выполнение этого процесса для любого порожденного от него объекта. А уже внутри конструктора, который унаследован от класса TObject, можно предусмотреть инициализацию переменных и выполнение дополнительных операций. Объявление конструктора выглядит следующим образом:
constructor Create;
В конструкторах потомков это объявление может перекрываться, но при необходимости вызвать конструктор предка используется оператор inherited:
... продолжение- Информатика
- Банковское дело
- Оценка бизнеса
- Бухгалтерское дело
- Валеология
- География
- Геология, Геофизика, Геодезия
- Религия
- Общая история
- Журналистика
- Таможенное дело
- История Казахстана
- Финансы
- Законодательство и Право, Криминалистика
- Маркетинг
- Культурология
- Медицина
- Менеджмент
- Нефть, Газ
- Искуство, музыка
- Педагогика
- Психология
- Страхование
- Налоги
- Политология
- Сертификация, стандартизация
- Социология, Демография
- Статистика
- Туризм
- Физика
- Философия
- Химия
- Делопроизводсто
- Экология, Охрана природы, Природопользование
- Экономика
- Литература
- Биология
- Мясо, молочно, вино-водочные продукты
- Земельный кадастр, Недвижимость
- Математика, Геометрия
- Государственное управление
- Архивное дело
- Полиграфия
- Горное дело
- Языковедение, Филология
- Исторические личности
- Автоматизация, Техника
- Экономическая география
- Международные отношения
- ОБЖ (Основы безопасности жизнедеятельности), Защита труда


