Санның логарифмі. Негізгі логарифмдік тепе - теңдік. Логарифмнің қасиеттері

С. Ешбаев атындағы орта мектебі

Бекітемін:

Оқу ісінің орынбасары А. Ж. Тулеуова

«» 2015 жыл

Тақырыбы: «Санның логарифмі.

Негізгі логарифмдік тепе - теңдік.

Логарифмнің қасиеттері»

Пәні: алгебра

Класы: 11

Өткізген: математика пәнінің мұғалімі

Қыйлыбаева Ақгүл

2015 - 2016 оқу жылы

Сабақтың тақырыбы: Санның логарифмі. Негізгі логарифмдік тепе-теңдік. Логарифмнің қасиеттері.
Сабақтың мақсаты:
1. Білімділігі: Оқушыларға логарифм ұғымын, логарифмнің анықтамасын, қасиеттерін беру, оларды тепе-тең түрлендіруде қолданады, білім, білік, дағдысын меңгереді;
2. Дамытушылығы: Оқушылар өз бетінше оқып, есеп шығару барысында ойлау қабілеттерін дамыта отырып, уақытты үнемді пайдалану дағдысын қалыптастырады;
3. Тәрбиелігі: Оқушылар ұйымшылдыққа, шапшаңдыққа, сыйластыққа тәрбиеленеді.
Сабақтың типі: Жаңа сабақты меңгерту
Сабақтың әдісі: Сын тұрғысынан ойлау (жеке, жұппен, топпен жұмыс істеу)
Қолданылатын стратегиялар: Білемін, білгім келеді, үйрендім. Топтастыру .
Сабақтың көрнекілігі: интерактивтік тақта, проектор, дербес компьютер, презентация, жұмыс парағы.
Сабақ барысы:
Ұйымдастыру:

А) Сәлемдесу,
Ә) сабақтың тақырыбын, мақсатын хабарлау.

І. Қызығушылыкты ояту.
Дәреженің негізі және көрсеткіші жөнінде не білеміз? Қасиеттер жөнінде не айтуға болады?
а ^т *а ^п =а ^т+п ; а ^т : а ^п =а ^т-п ; ( а ^т ) ^п =а ^тп ; Бұл жерде біз негізі мен дәреже көрсеткішіне қатысты қарастырып отырмыз. Математикада дәрежеге шығару амалы ретінде 7- сыныптан білеміз. Ал дәрежелеу амалына кері амал бұл түбір шығару у = = 5 математикалық алтыншы амал.
Қазір біз жетінші амал- логарифм табу амалын қарастырайық. Ол үшін дәреже, дәреженің негізі, саны арасындағы байланысты табу керек.
ІІ. Мағынаны тану кезеңі
Мыналарға жауап іздейік:
1. Логарифм табу дәрежеге шығаруға кері амалдардың бірі
2. Логарифмнің негізгі тепе-теңдігі
3. Логарифмнің негізгі қасиеттері
4. Түбір шығару мен логарифмді табу бір -бірінен өзгеше
Анықтама: Қандай да бір а санын х дәрежеге шығару арқылы алынған в санын а ^х =b (1)
теңдеуі түрінде жазуға болады, мұндағы а мен b -берілген сандар, ал х - белгісіз шама.
1) Бұл теңдеудің а 0, ал b 0 болса (1) теңдеуінің шешімі жоқ.
2) Егер а 0, b 0 болып, а 0 болса, теңдеудің бір ғана түбірі болады.
Анықтама: b саны шығу үшін а негізі шығарылатын х дәреже көрсеткішін b оң санының а негізі бойынша логарифмі деп атайды.
Ioq _a b=x жазуы негізі а болатын b санының логарифмі х -ке тең деп оқылады. Жауабымызды тақтамен салыстырамыз.
Мысал: Негізі 3 болатын 9 санының логарифмі 2-ге тең, себебі: 3 ² = 9 немесе Ioq ₃ 9=2,
Негізі 3 болатын 81 санының логарифмі 4-ге тең, себебі: 3 ⁴ = 81 Ioq ₃ 81=4, Негізі 3 болатын санының логарифмі -3-ке тең, себебі: 3 ^-3 = ; Ioq ₃ =-3.

Санның логарифмінің анықтамасынан а ^Ioq _a ^b =b (2) теңдігі шығады.
(2) теңдігін логарифмнің тепе-теңдігі деп атайды.

Мысал: 5 ^Ioq ₅ ⁹ =9; 4 ^Ioq ₄ ⁶ =6; 32 ^Ioq ₃₂ ⁶ =6

Логарифмнің қасиеттері:

1 ⁰ . Негізі а болатын а санының логарифмі 1 -ге тең : Ioq _a а=1
Ioq ₂ 2=1; Ioq ₃ 3=1; Ioq ₇ 7=1; Ioq ₃₆ 36=1; Ioq ₄₁ 41=?; Ioq ₅ 5=? Ioq ₃₆ 36=?; Ioq ₄ 4=?
2 ¹ =2, 3 ¹ =3, 7 ¹ = 7, 36 ¹ =36, 41 ^? =41, 5 ^? =5, 36 ^? =36, 4 ^? =4

2 ⁰ . Негізі а болатын 1 санының логарифмі 0 -ге тең: Ioq _a 1=0
Ioq ₂ 1=0, Ioq ₃₂ 1=0; Ioq ₇ 1=0; Ioq ₃₆ ?=0; Ioq ₄₁ ?=0; Ioq ₅ ?=0, Ioq ₃ ?=0; Ioq ₄ ?=0
2 ⁰ =1, 32 ⁰ =1, 7 ⁰ = 7, 36 ⁰ =?, 41 ⁰ =?, 5 ⁰ =?, 3 ⁰ =?, 4 ⁰ =?

3 ⁰ . Негіздері бірдей бірнеше оң санның көбейтіндісінің логарифмі көбейткіштердің логарифмдерінің қосындысына тең:
Ioq _a (bс) = Ioq _a b+ Ioq _a с

Ioq ₂ (4*8) = Ioq ₂ 4+ Ioq ₂ 8=2+3=5
Ioq ₁₂ (144*1728) = Ioq ₁₂ 144+ Ioq ₁₂ 1728=2+3=5
Ioq ₅ 125+ Ioq ₅ 625= Ioq ₅ (125*625) = Ioq ₅ (78125) =7

4 ⁰ . Бөлшектің логарифмі алымының логарифмі мен бөлімінің логарифмінің айырымына тең:
Ioq _a =Ioq _a d- Ioq _a b

Ioq ₉ 45- Ioq ₉ 5= Ioq ₉ = Ioq ₉ 9=1
Ioq ₂ 128- Ioq ₂ 4= Ioq ₂ = Ioq ₂ 32=5, Ioq ₂ 128- Ioq ₂ 4=7-2=5
Ioq ₃ 729- Ioq ₃ 9= Ioq ₃ = Ioq ₃ 81=4, Ioq ₃ 729- Ioq ₃ 9=6-2=4

5 ⁰ . Дәреженің логарифмі дәреже көрсеткішін дәреже негізінің логарифміне көбейткенге тең:
Ioq _a b ^п =пIoq _a b
Ioq ₃ 5 ² =2Ioq ₃ 5
Ioq ₄ 3 ² =Ioq ₄ 9 Ioq ₄ 3 ² =2Ioq ₄ 3
Ioq ₅ 125=Ioq ₅ 5 ³ =3Ioq ₅ 5=3*1=3
6 ⁰ . Жаңа негізге көшу формуласы: Ioq _a b= , Ioq _a b= ;

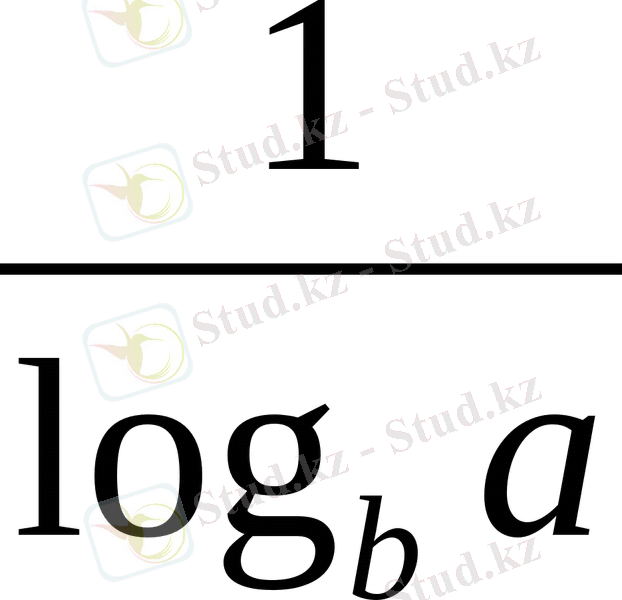Ioq ₁₀₀ 16= ; Ioq ₉ 3= ;
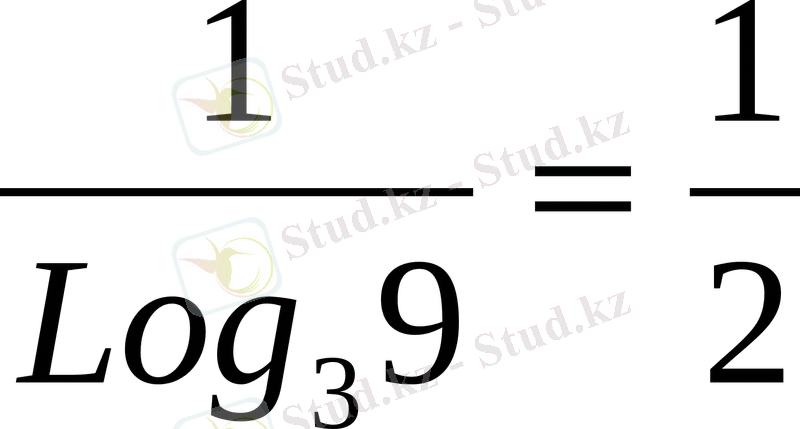Ioq ₆₄ 2= 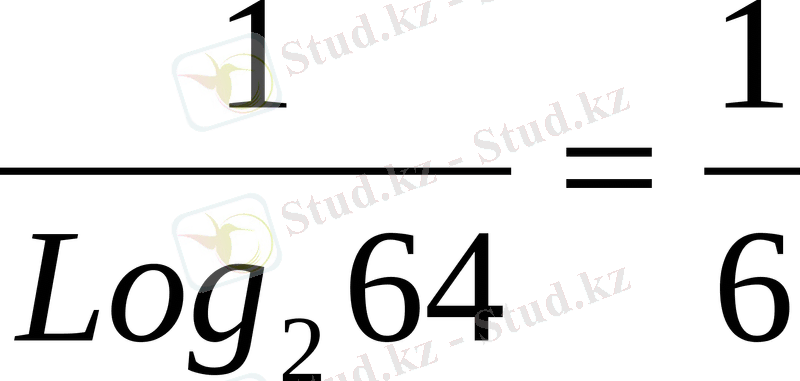; Ioq ₁₂₅ 5=
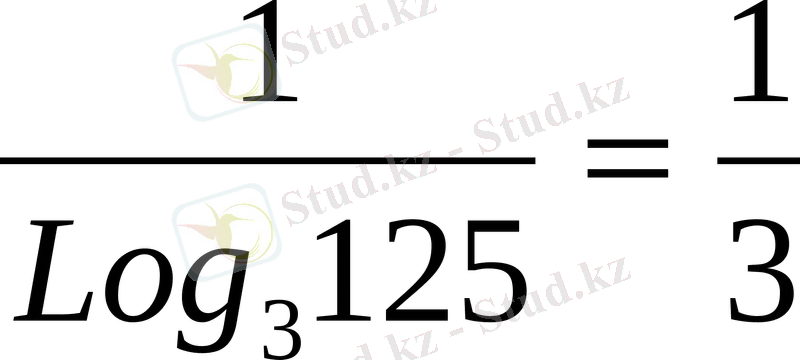
Логарифм табудың осы қасиеті кез келген алгебралық өрнекті логарифмдеу кезінде қолданылады.
Сонымен логарифмдеу дегеніміз-санның немесе өрнектің логарифмін табу, амалы, ал логарифмге кері амал - потенциалдау. Потенциалдау деп санды немесе өрнекті оның логарифмі бойынша табу амалын атайды.
Ioq _a х= Ioq _a т+ Ioq _a п- Ioq _a с ³ = Ioq _a ; Негіздері бірдей болғанда х = деп жазып есептейміз.
Қолданбалы мақсатта негіздері а = 10, а = е тең болатын логарифмдер жиі кездеседі.
Анықтама: Негізі 10 болатын санның логарифмі ондық логарифм де аталады. Ондық логарифмді жазу үшін Ig белгісі қолданылады. Ioq ₁₀ 81 орнына Ig81 деп жазылады (негіздегі ондық жазылмайды) . Есептеуді жеңілдету үшін ондық логарифмді қолданған ыңғайлы. (14-слайд)
Ондық логарифмнің өзіне тән үш қасиеті бар:
1 ⁰ . Бір саны және одан алдындағы нөлдерден тұратын оң ондық бөлшектің ондық логарифмі п болады, яғни а = 10 ^п , болса, онда Ig 100 = Ig10 ² = 2 ; Ig 1000 = Ig10 ³ = 3; Ig 1 = Ig10 ^? = ?; Ig 1 = Ig10 ^? = ?
2 ⁰ . Бір саны және оның алдындағы нөлдерден тұратын оң ондық бөлшектердің ондық логарифмі нөлдердің санына тең бүтін оң сан болады, яғни а = 10 ^-п , болса, онда Ig а = Ig10 ^{-

п} =- п; Ig 0, 1 = Ig10 ^{-

1} =- 1; Ig 0, 001 = Ig10 ^{-

3} =- 3 Ig 0, 0001 = Ig10 ^? =- ?, Ig 0, 01 = Ig10 ^? =?
3 ⁰ . 10 санының бүтін немесе нөлінші дәрежеге тең емес рационал санның ондық логарифмі иррационал сан болады. Мысалы:Ig 6, Ig 115, Ig 0, 12 Ig 3, 15