11-сыныпқа арналған сабақ жоспары: Логарифмдік теңсіздіктерді шешу

17. 02. 16 ж 11 сынып алгебра және анализ бастамалары

Сабақтың тақырыбы : Логарифмдік теңсіздіктерді шешу.

Сабақтың мақсаты:

Логарифмдік теңсіздіктерді шешу әдістерін, жолдарын үйрету, дағдыландыру.
Оқушылардың алған білімдерін практикада қолдана білу іскерліктерін, дағдыларын дамыту
Өзіндік ізденіс, оқушыларды белсенділікке, жинақтылыққа, математикалық тілде сөйлей білуге тәрбиелеу.

Сабақтың көрнекілігі және керекті құрал жабдықтар : интерактивті тақта, үлестірмелі дидактикалық кеспе қағаздар,

Сабақтың түрі :аралас сабақ.

Сабақ әдісі: топтық жұмыс, деңгейлеп оқыту, ой қозғау т. с. с

Сабақтың барысы:

Ұйымдастыру бөлімі. ( сабаққа қатысуын тексеру, дайындығын қадағалау, топқа бөлу т. с. с)
Үй тапсырмасын тексеру. № 449 Теңдеулер жүйесін шешу.

А) $\left\{ \begin{array}{r} \mathbf{4}^{\mathbf{х + у}}\mathbf{=}\mathbf{2}^{\mathbf{у - х}} \\ \mathbf{4}^{\mathbf{\log}_{\sqrt{\mathbf{2}}}\mathbf{х}}\mathbf{=}\mathbf{у}^{\mathbf{4}}\mathbf{- 5} \end{array} \right. \$

Шешуі: $\left\{ \begin{array}{r} \mathbf{4}^{\mathbf{х + у}}\mathbf{=}\mathbf{2}^{\mathbf{у - х}} \\ \mathbf{4}^{\mathbf{\log}_{\sqrt{\mathbf{2}}}\mathbf{х}}\mathbf{=}\mathbf{у}^{\mathbf{4}}\mathbf{- 5} \end{array} \right. \ \mathbf{\ \leftrightarrow}\left\{ \begin{array}{r} \mathbf{2}^{\mathbf{2х + 2у}}\mathbf{=}\mathbf{2}^{\mathbf{у - х}} \\ \mathbf{х}^{\mathbf{4}}\mathbf{-}\mathbf{у}^{\mathbf{4}}\mathbf{= - 5} \end{array}\mathbf{\leftrightarrow}\left\{ \begin{array}{r} \mathbf{2х + 2у = у - х} \\ \mathbf{х}^{\mathbf{4}}\mathbf{-}\mathbf{у}^{\mathbf{4}}\mathbf{= - 5} \end{array}\mathbf{\leftrightarrow}\left\{ \begin{array}{r} \mathbf{3х + у = 0} \\ \mathbf{х}^{\mathbf{4}}\mathbf{-}\mathbf{у}^{\mathbf{4}}\mathbf{= - 5} \end{array} \right. \ \right. \ \right. \$

$\mathbf{у = - 3х; \ }\mathbf{х}^{\mathbf{4}}\mathbf{- 81}\mathbf{х}^{\mathbf{4}}\mathbf{= - 5, \ 80}\mathbf{х}^{\mathbf{4}}\mathbf{= 5, \ }\mathbf{х}^{\mathbf{4}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{16}}$ , х $\mathbf{=}\frac{\mathbf{1}}{\mathbf{2}}\mathbf{, \ х = -}\frac{\mathbf{1}}{\mathbf{2}}$ бұдан у $\mathbf{=}\frac{\mathbf{3}}{\mathbf{2}}\mathbf{= - 1, 5}$ ;

жауабы: $\left( \mathbf{0, 5; - 1, 5} \right)$

№448 Теңдеулер жүйесін шешу.

Б) $\left\{ \begin{array}{r} \lg{\left( x^{2} + у^{2} \right) = 1 - \lg 8}\ \\ \lg{(х + у) - \lg{(х - у) = \lg 3}} \end{array} \right. \ \leftrightarrow \left\{ \begin{array}{r} x^{2} + у^{2} = \frac{5}{4} \\ \frac{х + у}{х - у} = 3 \end{array} \leftrightarrow 3х - 3у = х + у, х = 2у, \ \ \ 4у^{2\ } + \right. \ у^{2} = \frac{5}{4}$

5 $у^{2} = \frac{5}{4}\, \ у_{1} = \frac{1}{2}\ ; у_{2} = - \frac{1}{2}\ \ бұдан\, \ х_{1} = 1, \ х_{2} = - 1$ логарифмнің қасиеті бойынша теңдеулер жүйесінің шешімі: $(1; 0, 5)$

Жаңа тақырып:

Логарифмдік теңсіздіктерді шешу.

Әр топқа тапсырмалар беріледі.

9. Теңдеуді шешіңіз: log ₅ (2x+3) 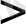log ₅ (x-1)

13. Теңсіздікті шешіңіз: lg(x+1) >lg(5-x) топ мүшелері теңсіздіктің шешімін тауып жауап береді.

Оқулықпен жұмыс. №462 а) , в) №464 а) және в)

№462 а) $\log_{3}{(5х - 2) > 1}$ жауабы: $(1; \infty)$

В) $\log_{0, 5}{\left( x^{2} - 5х + 7 \right) \geq 0\ \ ; жауабы:\ \lbrack 2; 3\rbrack}$

№464 а) $\log_{2}(3х - 2) < \log_{2}(2х - 3)$ ; жауабы: $\varnothing$

В) $\ln{х - \ln{(2х - 5) \leq \ln{2 - \ln(х - 3) }}}$ ; жауабы: $\left\rbrack 3; 5 \right\rbrack$

Тақырыпты бекіту. Бұл кезеңде оқушылардың логикалық ойлау қабілетін және белсенділігін арттыру мақсаты іске асты. Тақырыпқа байланысты тест жинағынан ҰБТ есептерін шығару арқылы жаңа тақырып бекітіледі.

Сабақты пысықтау сұрақтары:

Логарифмдік функцияның негізгі қасиеттері.
Негізгі логарифмдік теңбе теңдіктер.
Логарифмдік теңсіздіктің шешімін табуда логарифмдік функцияның қандай қасиетіне назар аудару керек?

Үйге тапсырма: №462, №464 қалғандары

Бағалау.

Ұқсас жұмыстар

11-сынып: Көрсеткіштік және логарифмдік теңсіздіктерді шешуге арналған сабақ жоспары

11-сыныпқа арналған алгебра: логарифмдік теңдеулер және оларды шешу тәсілдері

10-сыныпқа арналған Тригонометриялық теңсіздіктерді шешу сабақ жоспары

11-сынып: логарифмдік теңдеулер және шешу тәсілдері

Ашық сабақ: Көрсеткіштік және логарифмдік теңдеулерді шешу (Алгебра, 11-сынып)

11-сыныпқа арналған ашық сабақ: Логарифмдік теңдеулерге есептер шығару

Логарифмдік теңдеулерді шешу: сабақ жоспары мен тапсырмалар

11-сынып алгебра: логарифмдік теңдеулерді шешуге арналған сабақ жоспары

Теңсіздіктерді интервалдар әдісімен шешу: сабақ жоспары