Пифагор теоремасына кері теорема

Күні. ___________
Сыныбы: 8
Пәні: геометрия
Сабақтың тақырыбы: Пифагор теоремасына кері теорема
Мақсаты: 1) Пифагор теоремасын және кері теореманы есептер шығаруда қолдана білу дағдысын қалыптастыру.
2) Танымдық, іздемпаздық, пәнге деген ынтасын арттырып, шығармашылыққа баулып, өз бетімен танып білім жетілдіру.
3)Ұқыптылыққа, ұйымшылдыққа, өз бетімен жұмыс жасауға тәрбиелеу.
Сабақтың түрі: Аралас сабақ
Көрнекілігі: Сызбалар, сызғыш, циркуль
Сабақтың барысы: 1. Ұйымдастыру
2. Үй тапсырмасын сұрау
№
Жаңа сабақты баяндау. Пифагор теоремасы

1-мысал. АВС тікбұрышты үшбұрышының бір бұрышы , с-гипотенуза, a, b-катеттері, ал a1 және b1 гипотенузаға түсірілген a мен b катеттерінің проекциялары болса,
1) ; 2)
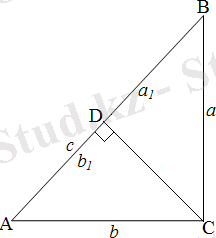формулаларының дұрыс болатынын дәлелдейік.

Шешуі: екені белгілі (Пифагор теоремасының дәлелдемесін қараңдар) катетінің гипотенузадағы проекциясы кесіндісі катетінің проекциясы кесіндісі болады, сондықтан немесе , бұдан ; дәл осылай немесе , бұдан дәлелдеу керегі де осы.
2-мысал. Радиусы 5 см-ге тең шеңбер центрінің бір жағында жататын, ұзындықтары 8 см және 6 см ені параллель хорда жүргізілген. Осы хордалардың арақашықтығын табайық.

Шешуі: АВ және СД хордаларына перпендикуляр OL радиусы жүргіземіз, шеңбердің О центрін С, А, D және B нүктелерімен қосамыз. (радиустар) болғандықтан, мен үшбұрыштары теңбүйірлі үшбұрыштар және мен -олардың биіктіктері. Теңбүйірлі үшбұрыштың табанына түсірілген биіктігі оның медианасы да болатыны белгілі. Сондықтан және . және тікбұрышты үшбұрышында , . үшбұрышынан Пифагор теоремасы бойынша немесе болады.
Ал үшбұрышынан мынаны аламыз: немесе болады, сонда хордалардың арақашықтығы
Жауабы: 1 см

Есептер шығару.
№
3 м
5 м
x
C
B
А
Тікбұрышты үшбұрыштың гипотенузасы 5 м, ал оның бір катеті 3 м. Екінші катетті табыңдар.

Шешуі: Пифагор
теоремасы бойынша

Жауабы: 4 м

№
Тіктөртбұрыштың бір қабырғасы 91 см, диагоналі 109 см болса, оның екінші қабырғасын есептеңдер.
x
91
D
С
В
А
109
Шешуі: Пифагор
теоремасы бойынша

Жауабы: 60 м

№132
Ромбының қабырғасы 13 дм, ал оның диагональдарының бірі 10 дм . Екінші

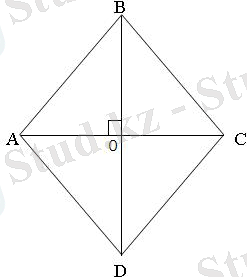
диогоналін табыңдар.

Шешуі: ромб,
Табу керек:

Жауабы: 24 дм

АВС тікбұрышты үшбұрыш, , катеттер, гипотенуза; сәйкес катеттердің гипотенузаға түсірілген проекциялары 1) егер болса, неге тең?

Шешуі: 1-мысалдағы формулаларды қолданамыз: және

Пифагор теоремасынан

Жауабы: 7,5 см; 10 см; см

№135
1) деп алып, және катеттері бойынша тікбұрышты үшбұрыштың гипотенузаға түсірілген биіктігін табыңдар.

Шешуі:

Жауабы:
Қорытындылау.
Пифагор теоремасы көптеген есептер шығаруда қолданылады. Пифагор теоремасын дәлелдеудің жолдары өте көп. Пифагор жайлы және оның теоремасын дәлелдеу жолдарын өз беттеріңше ізденіп, осы тараудың аяғында қорытынды сабаққа дайындап әкеліңдер.
Үйге тапсырма беру
№