Геометрияға байланысты логикалық есептер жүйесі мен шығару жолдары

<<Майқарағай жалпы орта білім беретін мектеп>> мемлекеттік мекемесі

Баяндама:
Геометрияға байланысты логикалық есептер жүйесі мен шығару жолдары

Математика пәні мұғалімі: Ерғазина Ә.М.

Геометрияға байланысты логикалық есептер жүйесі мен шығару жолдары

Оқу процесінде есеп шығару математиканы оқыту мақсаты ретінде де, оны оқыту әдісі ретінде де бой көрсетеді. <<Математикалық есеп дегеніміз - математикадағы заңдылықтар, ережелер мен тәсілдер негізінде оқушылардын ойы мен іс-әрекетін талап ететін және математикалық білімді меңгеруге, оларды практикада қолдана білуге дағдыландыруға, ойлау қабілетін дамытуға бағытталған ситуация>>. Сондықтан есеп шығару математикалық ұғымдарды қалыптастырып, байытуға оқушылардың математикалық ойлауын өрістетуіне, білімдерін практикада қолдануға, табандылық, ізденгіштік, еңбексүйгіштік қасиеттерін тәрбиелеуге жол ашады. Сонымен бірге, есеп шығару процесінде оқушылар практикалық біліктер мсн өмірде өздеріне керекті дағдыларды игереді пайдалы фактілермен танысады. Өмірде жиі кездесетін шамалардың арасындагы байланыстар мен тәуелділіктерді тағайындауға үйренеді.
Есеп оқушыларды жаңа математикалық біліммен қаруландырып, қалыптасқан іскерліктері мен машықтарын жүйелеуге және нақтылауға көмектеседі. Математиканы оқытудың жалпы системасында есептер шығару тиімді жаттығулардың бір түрі болып табылады.
Есептер шығарудың ең әуелі балаларда толық бағалы математикалық ұғымдарды қалыптастыруда, олардың бағдарлама анықтап берген теориялық білімді игеруде өте маңызды мәні бар.
Геометриялық есептерді шешу барысында оның шартын өзгерту арқылы әртүрлі зерттеу жұмысын жүргізуге болады. Есеп шартында қолданылмаған информацияны зерттеп, ойымызды дамытатын басқа да есептер құрастыруға болады. Мұндай зерттеуге келтірілетін есептер жазықтықтағы салу және кеңістіктегі салулар болып табылады. Жазықтықтағы салулар белгілі аспаптардың көмегімен салынатын болса, кеңістікте мұндай салу аспаптары жоқ, тек аксиомалардың көмегімен салу, түрлендіру, есептері күрделі қатынастарды есептеуге берілген есептер зерттеудің қайнар көзі.
Геометрия есептері әр түрлі ізденістерімен жаңалықтар ашуға итермелейді. Кез-келген геометриялық есепті шешу кезінде соған сәйкес геометриялық фигураның әр алуан касиеттері анықталады. Бұл қасиеттер ең болмағанда есептің сұрағына жауап беруге қажетті және жеткілікті болады. Жалпы алғанда есепті шешу кезінде оған қолданылмайтын басы артық қасиеттерде кездесуі мүмкін. Әр түрлі көзқарас тұрғысынан алғанда маңызды болып табылатын, есеп шартында көрсетілмеген геометриялық фигураның қасиеттерін іздеген кезде ғана геометриялық есептерді зерттеу басталады. Мұндай зерттеу осы есептің шешілуімен тікелей байланысты. Есепті зерттеу барысында фигураның әр түрлі қызықты қасиеттерін іздеумен шектелуге болады. Геометриялық фигурадан табылған жаңа касиеттерді берілген есептің басқа жаңа шешімдерін іздеуге, жаңа есептер құрастыруға болады. Геометрияның мектептегі курсы оқушыларды математикалық тұжырымдарды жалпылай білу дағдысын үйретеді.
Жалпылаудың түрлері төмендегідей:
1. Бір есепті не теореманы қарастыру негізінде
* дәлелдеу мен есеп шешімін тікелей үйрену;
* есепті қайта тұжырымдау арқылы жалпылау.
2. Мұғалім ұсынған бірнеше дербес жағдайларды, үйрену арқылы жалпылау.
3. Жалпы теореманың дербес жағдайларын табу
4. Есептерді талдау мен шешуге негізделіп берілгендерге керісінше алынған мәліметтер бойынша есептер құрастыру.
Жазықтықтағы фигуралардың аудандарын табу
1 - есеп
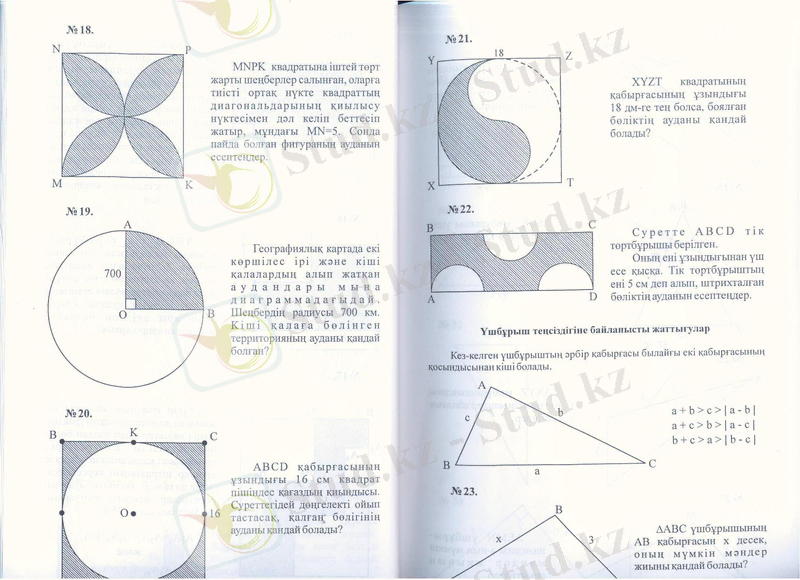
MNPK квадратына іштей жарты шеңберлер салынған. Оларға тиісті ортақ нүкте квадраттың диагональдарының қиылысу нүктесімен дәл келіп беттесіп жатыр, мұндағы MN=5. Сонда пайда болған фигураның ауданын есептеңдер.

MNPK - квадрат. PK=5 квадратқа іштей 4 жарты шеңбер салынған. Штрихталған бөліктің ауданын табу керек.
Шешуі: SMNPK - 2S жарты дөңг. = 2 S жарты дөңгелектің радиусы 2,5-ке тең.
2S=25-PI2,52=25 - 6,25 PI. MNPK квадратының ауданы төрт еселенген S аудандары мен ізделінді фигураның ауданының қосындысына тең. Олай болса,

S ізд.ф = SMNPK - 4S = 25-2(25 - 6,25 PI) = 25-50+12,5 PI = -25+12,5 PI
Жауабы: 12,5( PI - 2) кв.б.

Координаталары бойынша нүктені салу

№2-есеп
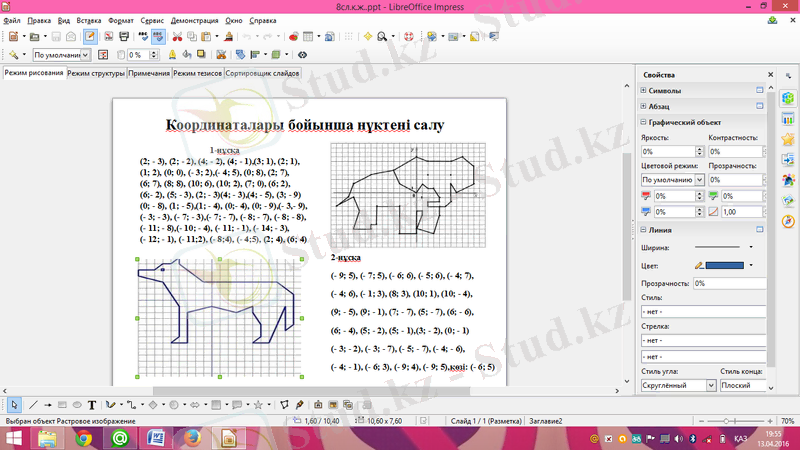
(2; - 3), (2; - 2), (4; - 2), (4; - 1),(3; 1), (2; 1),
(1; 2), (0; 0), (- 3; 2),(- 4; 5), (0; 8), (2; 7),
(6; 7), (8; 8), (10; 6), (10; 2), (7; 0), (6; 2),
(6;- 2), (5; - 3), (2; - 3)(4; - 3),(4; - 5), (3; - 9)
(0; - 8), (1; - 5),(1; - 4), (0;- 4), (0; - 9),(- 3,9),
(- 3; - 3), (- 7; - 3),(- 7; - 7), (- 8; - 7), (- 8; -8),
(- 11; - 8),(- 10; - 4), (- 11; - 1), (- 14; - 3),
(- 12; - 1), (- 11;2), (- 8;4), (- 4;5), (2; 4), (6; 4)

№3-есеп

(- 9; 5), (- 7; 5), (- 6; 6), (- 5; 6), (- 4; 7),
(- 4; 6), (- 1; 3), (8; 3), (10; 1), (10; - 4),
(9; - 5), (9; - 1), (7; - 7), (5; - 7), (6; - 6),
(6; - 4), (5; - 2), (5; - 1),(3; - 2), (0; - 1)
(- 3; - 2), (- 3; - 7), (- 5; - 7), (- 4; - 6),
(- 4; - 1), (- 6; 3), (- 9; 4), (- 9; 5),көзі: (- 6; 5)

Салу есептері
№4-есеп
Қабырғасы және диагоналі бойынша ромб салыңдар
Салу жолы: 2 жағдай қарастырамыз. d1=
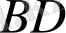
1. е сәулесін саламыз
2. сәуледен =а кесіндісін өлшеп саламыз
3. шеңбер саламыз, ВEuro болады
4.
5.
6. жүргіземіз
7. жүргіземіз
8. деп белгілейміз. - ізделінді ромб.
Ромб екенін дәлелдейміз. Салуымыз бойынша
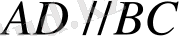
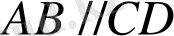бұдан 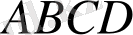параллелограмм
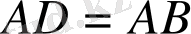болғандықтан 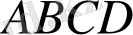ромб

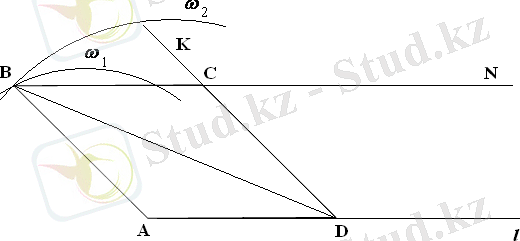
ІІ жағдай
d1=АС диагональ болса
1. е сәулесін саламыз;
2. сәуледен =а кесіндісін өлшеп саламыз,
3. шеңбер саламыз, СEuro;
4. ;
5. ;
6. жүргіземіз;
7. жүргіземіз;
8. ізделінді ромб.

№5-есеп
Радиусы 5 см-ге тең шеңбер центрінің бір жағында жататын, ұзындықтары 8 см және см ені параллель хорда жүргізілген. Осы хордалардың арақашықтығын табайық :
Шешуі: АВ және СД хордаларына перпендикуляр OL радиусы жүргіземіз, шеңбердің О центрін С, А, D және B нүктелерімен қосамыз. (радиустар) болғандықтан, мен үшбұрыштары теңбүйірлі үшбұрыштар және мен -олардың биіктіктері. Теңбүйірлі үшбұрыштың табанына түсірілген биіктігі оның медианасы да болатыны белгілі. Сондықтан және . және тікбұрышты үшбұрышында , . үшбұрышынан Пифагор теоремасы бойынша немесе болады.
Ал үшбұрышынан мынаны аламыз: немесе болады, сонда хордалардың арақашықтығы
Жауабы: 1 см
Осы айтылған жалпылауларға сүйеніп кұрастырылған есептер окушы білімін тереңдетіп, өзбетінше танымдық әрекетінің сапасын көтереді.
Қорытынды: Геометрия есептерінің шарттарын қалағанымызша өзгерту арқылы арнайы зерттеу жұмысын жүргізуге болады. Геометрия есептері - зерттеу жүргізудің негізі.