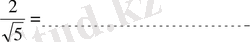8-сынып: Квадрат түбірлері бар өрнектерді түрлендірудің қорытынды практикалық сабағы

Сынып: 8г

Сабақ тақырыбы: Квадрат түбірлері бар өрнектерді түрлендіру.

Сабақ типі: қорытындылау сабағы

Түрі: практикалық

Сабақ мақсаттары:

білімділік -оқушылардың тақырып бойынша алған білімдерін тереңдетіп, жинақтау, жүйелеу, бекіту.
дамытушылық -логикалық ойлау қабілеті мен дағдыларын жетілдіру, белсенділіктерін, математикаға деген қызығушылықтарын арттыру;
тәрбиелік -оқуға, саналы сезімге, жауапкершілікке, өз бетінше еңбектенуге тәрбиелеу.

Сабақ көрнекілігі: компьютер, интерактивті тақта, карточкалар.

Сабақ әдістері : ауызша, көрнекілік, өз бетімен жұмыс, топпен жұмыс.

Сабақ барысы:

1. Ұйымдастыру. (4 мин)

2. Ой қозғау ( 10 мин)

3. « Сен-маған, мен -саған» ( 15 мин)

4. «Сергіту сәті» (2 мин)

5. «Біліміңді сынап көр»оқулықпен жұмыс. (6 мин)

7. қорытынды.

8. Ү й жұмысы.

« Адамның даңқы оның ойлау қабілетінде» Паскаль

Ұйымдастыру кезеңі. Сәлеметсіздер ме, балалар! Отырыңыздар. Балалардың сабаққа даярлығын тексеру. Бүгінгі біздің тақырыбымыз: «Квадрат түбірлері бар өрнектерді түрлендіру. Бүгін біз сабақта түрлендірудің қасиеттерін қайталаймыз.

Арифметикалық квадрат түбір:

\[{\sqrt{a}}=b\]

мұндағы а = в ² , а ≥ 0, в ≥ 0

Арифметикалық квадрат түбірдің қасиеттері:

\[{\sqrt{a b}}={\sqrt{a}}\cdot{\sqrt{b}}\]

\[a^{3}\ 0,b\ \geq0\]

\[{\sqrt{\frac{a}{b}}}={\frac{\sqrt{a}}{\sqrt{b}}}\]

\[(a\,^{3}\,\cup,b\,\geq0)\]

\[{\sqrt{a^{2n}}}=a^{n}\]

\[a\geq0\]

\[{\sqrt{a^{2}}}=\left|a\right|\]

І. Ой қозғау ( 10 мин) Конверт- сұрақ стретегиясы, конвертке өткен тақырыптар бойынша 3 сұрақ жазып барлық тортарға таратады. Жеке, жұптық, топтық жұмыс.

\[{\sqrt{0.64a^{6}}}=......\]

\[{\sqrt{369times256}}=\ldots\ldots\ldots-\]

\[{\sqrt{82^{2}-16^{2}}}=.......\]

\[{\sqrt{\frac{25\sqrt{64}}{16}}}=......\]

\[{\sqrt{8}}\times{\sqrt{2}}=_{\circ\circ\circ\circ\circ\circ\circ}\]

А) Арифметикалық квадрат түбірдің анықтамасы.

В) Арифметикалық квадрат түбірдің қасиеттері.

С) Квадрат түбірлері бар өрнектерді түрлендірудің тәсілдерін ата.

Д) Әрбір тәсіл жайлы ашып айт.

1. Арифметикалық квадрат түбірдің анықтамасын.

2. Көбейткішті түбір таңбасының алдына шығару ережесін.

3. Көбейткішті түбір таңбасының астына алу ережесін.

4. Көбейтіндіні қалай дәрежелейді?

5. Бөлшек санды қалай дәрежелеу керек?

ІІ. «Сен -маған, мен-саған» Деңгейлік тапсырмалар.

І кезең. Есіңе түсір

ІІІ кезең. Деңгейлік тапсырмалар.

деңгей. (5- ұпай)

1. Есепте:

\[\operatorname{OJS}(\log^{6}\mathbf{\nabla}-\sqrt{16a^{4}}\mathbf{\nabla}(\mathbf{\nabla}\cdot\mathbf{\operatorname{-}}\cdot\mathbf{\sqrt{}}\mathbf{\mathrm{-}}\cdot\mathbf{\mathrm{-}}\cdot\mathbf{\sqrt{}}\mathbf{\mathrm{-}}\cdot\mathbf{\mathrm{-}}\cdot\mathbf{\sqrt{}}\cdot\mathbf{\mathrm{-}}\cdot\mathbf{\sqrt{}}\cdot\mathbf{\hat{w}}\cdot\mathbf{\hat{w}}(\mathbf{\hat{--}})\]

2. Өрнектерді ықшамда:

\[{\sqrt{28}}\sim3{\sqrt{63}}=_{-<\cdots<\cdots<\cdots<\cdots<\cdots<\cdots<\cdots<\cdots<\cdots<\cdots<\cdots}\]

\[\frac{1}{x+y}\sqrt{2\bigl(x^{\ 2}+2x y+y^{\ 2}\bigr)}=_{\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\cdot\ldots}\]

\[(x:3){\sqrt{{\frac{3}{x^{2}\cdot6x+9}}}}=............................\]

5. Сандарды салыстыр:

а)

\[2{\sqrt{5}}\]

және 3

\[{\sqrt{3}}\]

ә)

\[12{\sqrt{20}}\]

және

\[\mathbf{1}{\sqrt{{\bf19}_{\cdot}...............+\cdot\cdot\cdot\cdot\cdot...-\cdot\cdot\cdot\cdot\cdot-\cdot\cdot\cdot\cdot-\cdot-\cdot-\cdot-\cdot-\cdot-\cdot-\cdot-\cdot-\cdot}}\]

б)

\[{\frac{1}{4}}{\sqrt{112}}\]

және

2-деңгей (10 ұпай)

Бөлімін иррационалдықтан арылт:

Теңдеуді шеш:

3-деңгей (15 ұпай)

1. Бөлшекті қысқарт:

\[\frac{\sqrt{a}+\sqrt{b}}{a\sqrt{a}+b\sqrt{b}}=_{\sim\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots}\]

2. Теңдеуді шеш:

\[{\big(}q+{\sqrt{x}}{\big)}8-{\sqrt{x}}{\big)}=1-x\]

Қате жіберген есептерді талқылау.

ІІІ . Сергіту сәті. Дұрыс жауапқа қолдарын жоғары көтереді, қате болса алға созады.

Бірдей көбейткіштерден тұратын көбейтінді дәреже д. а. (+)
Негіздері бірдей дәрежелерді көбейткенде, дәрежелерін қосамыз. (+)
Тік бұрыштың өлшемі 1800-қа тең. (-)
функциясының графигі парабола. (+)
функциясының графигі гипербола (-)
23=8 (+)
4*4=-16
(-5) 2=-25 (-)

6. Оқулықпен жұмыс. «Білімдіге - биіктен орын»

№84, №85(1, 3), №86 тақ

№84

$\mathbf{0, 5}\sqrt{\mathbf{80}}\mathbf{-}\frac{\mathbf{1}}{\mathbf{6}}\sqrt{\mathbf{180}}\mathbf{+ 9}\sqrt{\mathbf{605}}\mathbf{= 100}\sqrt{\mathbf{5}}$

$\frac{\mathbf{1}}{\mathbf{2}}\sqrt{\mathbf{1200}}\mathbf{-}\frac{\mathbf{2}}{\mathbf{5}}\sqrt{\mathbf{2700}}\mathbf{- 0, 4}\sqrt{\mathbf{243}}\mathbf{= - 5, 6}\sqrt{\mathbf{3}}$