Виет теоремасы және оның кері теоремасы: келтірілген квадрат теңдеудің түбірлерін табу және теңдеу құру


Сынып: 8 «ә» пән: алгебра
Сабақтың мақсаты: Виет теоремасын пайдаланып, келтірілген квадрат теңдеудің түбірлерін табуға және Виет теоремасына кері теореманы пайдаланып, квадрат теңдеу құруға үйрету.
Дамытушылық мақсаты:
1. Алған білімдерін әртүрлі жағдайда қолдана білуге дағдыландыру.
2. Белсенділігін көтеруге, ойлау қабілетін арттыруға, өз ойын жүйелеуге, тез шешім қабылдауға ұқсастықты, қарама-қайшылықты байқауға дағдыландыру.
Тәрбиелік мақсаты: Оқушылардың білімге деген қызығушылығын арттыру. Ұжым намысын қорғай білетін, шығармашылық қабілеті дамыған тұлға тәрбиелеу.
Сабақтың түрі: Жаңа сабақ
Әдісі: қызығушылықты ояту, «араласып кеткен оқиға» стратегиясы, «Иә, жоқ» стратегиясы.
Көрнекілігі:
1. Квадрат теңдеулердің түбірлерін табу формулалары.
2. Әр түрлі деңгейлік тапсырмалар жазылған үлестірмелер.
3. Плакаттар.
Сабақтың барысы:
І. Ұйымдастыру.
Сыныпты 3 топқа бөлемін. Топқа фигураларды таңдай отырып топқа бөлінеді. Және осы топтарға мінездеме беріледі. Топ басшысы сайланады. Бағалау парағы таратылып беріледі.
І Симатикалық картамен жұмыс.
ІІ. Өткен материалды еске түсіру.
Квадрат теңдеу дегеніміз не?
Квадрат теңдеудің түрлері?
Квадрат теңдеудің формулалары
ІІІ. Тарихи дерек (математик Франсуа Виет) туралы айту.
Француа Виет ( 1540-1603) -француз математигі, мамандығы бойынша заң қызметкері. Астрономияға қызығып оны терең үйрету үшін алгебрамен және тригонометриямен айналысқан. Ол бірінші болып әріптермен тек айнымалыларды ғана емес, берілген шамаларды да яғни теңдеудегі айнымалылардың коэффиценттерін де белгілеген. Оның еңбектерінде алгебра символиклық таңбаларға негізделген теңдеулер туралы жалпы ғылымға айналды. Осының арқасында теңдеу мен оның түбірлерінің жалпы қасиеттерін формуламен жазуға мүмкіндік туды. Алгебралық өрнектер амалдар қолдануға болатын болатын объектіге айналды. Математиканың қазіргі деңгейге жетуіне Виет енгізген жаңалықтардың шешуші әсері болды. Сондықтан европалықтар оны «алгебраның атасы» деп атаған.
ІV. Жаңа тақырып.
- квадрат теңдеудің түбірлерін қосайық
- квадрат теңдеудің түбірлерін көбейтейік
- екендігін көріп тұрмыз. Ендеше мынадай теорема шығады.
Теорема: Келтірілген квадрат теңдеудің түбірлерінің қосындысы қарама-қарсы таңбамен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең.
Егер келтірілген квадрат теңдеудегі
белгілесек, онда
,
.
Осы теореманы Виет теоремасы деп аталады.
D=0, Виет торемасын қолдануға болады ма?
теңдеуінің D=0 жағдайында өзара тең екі түбірі бар және олардың әрқайсысы
-ге тең.
Бұл екі түбірді
және
формуласынан
деп ұйғарып,
аламыз. D=0 жағдайы үшін де Виет теоремасы дұрыс. Расында

Виет теоремасына кері теорема да дұрыс.
Теорема. (Виет теоремасына кері теорема) . Егер екі санның қосындысы -р-ға, ал олардың көбейтіндісі q-ға тең болса, онда ол сандар
теңдеуінің түбірлері болады.
V. Деңгелік тапсырма.
А деңгейі
№147
В деңгейі
№159
1)
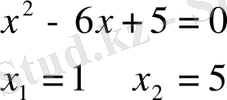 2)
2)
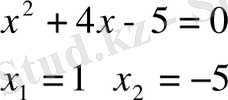 3)
3)
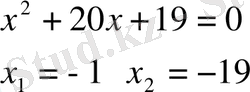 4)
4)
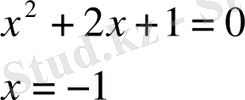
5)
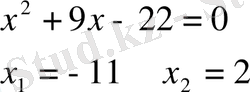 6)
6)
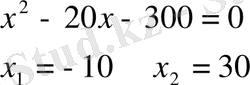
№160
1)
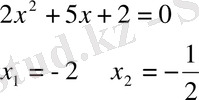 2)
2)
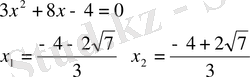 3)
3)
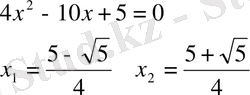 4)
4)
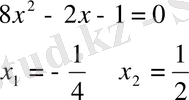 5)
5)
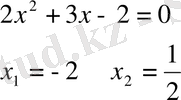 6)
6)
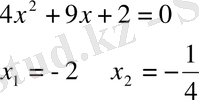
С деңгейі
№163

3)
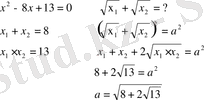 4)
4)
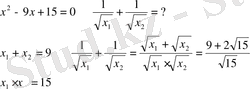
VІ. Сабақты бекіту.
- «Иә»немесе«Жоқ». ойыны.
Қатесін айтып дәлелдейді.
- Мен сіздерге мақал айтамын. Оның ішіндегі екі сан есім квадраттық теңдеудің түбірлері, яғни түбірлер арқылы квадраттық теңдеу құру керек?
- Алтауала болса ауыздағы кетеді, төртеутүгел болса төбедегі жетеді. (Б)
- Жетіжұрттың тілін біл, жетітүрлі білім ал. (І)
- Білімдімыңдыжығады, білектібірдіжығады. (Л)
- Ұлғаотызүйден, қызғақырықүйден тыю. (І)
- Біртал кессең, онтал ек(М)
VІІ. Қорытынды .
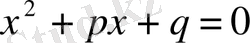 теңдеуінің х
1
және х
2
сандары түбірі болса, онда х
1
+х
2
=-р, х
1
*х
2
=q болады.
теңдеуінің х
1
және х
2
сандары түбірі болса, онда х
1
+х
2
=-р, х
1
*х
2
=q болады.
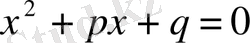 теңдеуінің х
1
, х
2
сандары түбірі болады.
теңдеуінің х
1
, х
2
сандары түбірі болады.
Бағалау.
Үйге тапсырма: № 149, №153
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz

