Түзулердің параллельдік белгілері

<<Бекітемін>> _______________директордың оқу ісі жөніндегі орынбасары
САБАҚ ЖОСПАРЫ

САБАҚ: Геометрия
№264 мектеп-лицей
Күні: 17.01.2017
Оқытушының аты-жөні: Жиенбаева Ботакөз Шаймағанбетқызы
СЫНЫП: 7
Барлық оқушы саны:
Қатыспағандар:
Сабақтың тақырыбы:
Түзулердің параллельдік белгілері
Сабақ негізделген оқу мақсаты
Түзулердің параллельдігінің белгілерімен танысып есептер шығаруда қолдану
Сабақтың мақсаттары
Барлық оқушылар:

Бірнеше түзу қиылысқанда пайда болатын бұрыштарды атап көрсете алады

Оқушылардың басым бөлігі:

Теоремаларды түсінеді, оларды қолданып түзулердің параллельдігін анықтай алады.

Кейбір оқушылар:

Ішкі тұстас бұрыштардың биссектрисаларының қандай бұрышпен қиылысатынын таба алады
Тілдік мақсат
Негізгі сөздер мен тіркестер:
Параллель түзулер, қиюшы, сәйкес бұрыштар, ішкі айқыш бұрыштар, ішкі тұстас бұрыштар, биссектриса, ...

Талдауға арналған тармақтар:
Параллельдік белгілерінің теоремалары

Жазылым бойынша ұсыныстар:
Есептер шығару, сызба сызу
Ресурстар
"Геометрия" оқулық, білім лэнд сайты, интербелсенді тақта, стикер, маркерлер.
Алдыңғы білім
параллель, қиылысушы түзулер, биссектрисаны салу.

Жоспарланған әрекеттер
Ресурстар
Басы
10 мин

І. Ұйымдастыру. Оқушылар тақтаға өздері жазған сандары бойынша топқа бірігеді
Әр оқушыға арналған жұмыс дәптерлері таратылып сол бойынша жұмыс жасайды.
ІІ. Қайталауға арналған сұрақтар.
"Зымыран сұрақтар" әдісі арқылы.

Ортасы
ІІІ. Тұсаукесер. (Жаңа тақырыпқа кіріспе)
6 сурет 1 жауап ойыны бойынша "параллель түзулер" тіркесін айқындау

Екі түзудің параллельдігін анықтау үшін не қажет? Геогебра бағдарламасын пайдаланып бір қарағанда паралель түзуге ұқсас болғанымен қиылысатын түзулер екендігін көз жеткізіп, параллельдіктің қандай белгілері бар екенін анықтау қажеттігін түсіндіру.

IV. Жаңа тақырып. Топтық жұмыс.
Әр топқа теоремаларды түсіндіріп сызбасын көрсету тапсырылады.

Теорема1. Егер екі түзудің әрқайсысы үшінші бір түзуге параллель болса, онда бұл екі түзу өзара параллель болады.
Теорема2. Егер екі түзуді үшінші түзу қиып өткенде айқыш бұрыштар тең болса, онда берілген екі түзу өзара параллель болады.
Теорема3. Егер екі түзуді үшінші түзу қиып өткенде сәйкес бұрыштар тең болса, онда берілген екі түзу өзара параллель болады.
Теорема4. Егер екі түзуді үшінші түзу қиып өткенде тұстас бұрыштардың қосындысы 1800-қа тең болса, онда берілген екі түзу өзара параллель болады.

Топтық жұмыстың бағалау критерийлері
oo Теореманың дұрыс берілуі 1 балл
oo Сызбаның дұрыс болуы 1 балл
oo Дәлелденуі 2 балл
oo Түсіндірілуі 1 балл
oo
V. Барлық дұрыс тұжырымдарды белгілеңіз
"Bilim land.kz" сайтының тапсырма

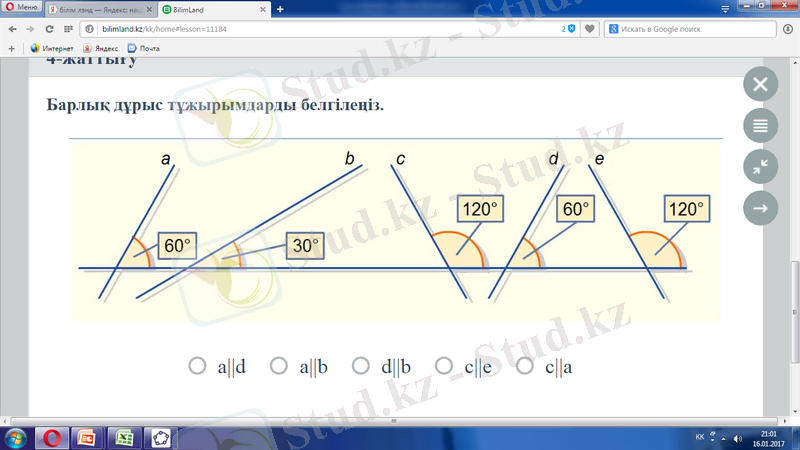
VІ Есептер шығару
oo Есеп шартының дұрыс берілуі 1 балл
oo Сызбаның дұрыс болуы 1 балл
oo Есеп шығарылуы 2 балл

№149 a, b, c түзулері d қиюшысымен қиылысқан .
∠1=42° , ∠2=140° , ∠3=138° a, b, c түзулерінің қайсысы параллель.
∠1 және ∠2 ішкі тұстас бұрыштар.
∠1+∠2=42°+140°=182°!=180, онда a∩b
∠2!=∠3 сәйкес бұрыштар тең емес. онда с∩b
∠1 және ∠3 ішкі тұстас бұрыштар.
∠1+∠3=42°+138°=180°, онда a∥с.
№161 Екі параллель түзуді үшінші түзумен қиғанда пайда болатын ішкі тұстас бұрыштардың биссектрисалары қандай бұрышпен қиылысады?
Шешуі:
∠3=х° ∠5=180-х°
∠3:2=х°/2 ∠5:2=180-х°2
∠9=180-(∠3:2+∠5:2)=х°2 +180°-х°2=90°

Соңы
І. Қорытынды.
Орындалған әрбір тапсырманы оқушы өзін-өзі түсінуіне қарай бағалау жүргізіледі.

Үйге тапсырма
1) Түзулердің параллельдік белгілері
2) №160 есептердің жұптарын аяқтап шығару
Бағалау.

Рефлексия
Сабақ мақсаттары/оқыту мақсаттары жүзеге асырымды болды ма?
Бүгін оқушылар нені үйренді?
Оқыту ортасы қандай болды? Менің бөліп оқытқаным өз мәнінде жүзеге асты ма?
Мен өз уақытымды ұтымды пайдалана алдым ба?
Мен жоспарыма қандай өзгерістер енгіздім және неліктен?

Қорытынды бағалау
Ең жақсы өткен екі тапсырманы атап көрсетіңіз (оқытуға және үйренуге қатысты)
1:

2:

Қандай екі нәрсе немесе тапсырма сабақтың одан да жақсы өтуіне ықпалын тигізер еді (оқытуға және үйренуге қатысты)?
1:

2:

Осы сабақтың барысында барлық сынып немесе жекелеген оқушылар туралы менің келесі сабағыма қажет болуы мүмкін қандай ақпаратты білдім?
1:

2: