Квадрат тендеуге келтірілетін тендеулер

Мұхит атындағы жалпы орта білім беретін мектебі

Сабақтың тақырыбы

[pic]

8-а сынып

Пән мұғалімі Ш Искакова

Cабақтың тақырыбы: Квадрат тендеуге келтірілетін тендеулер.

Сабақтың мақсаты:

1)Оқушылардың квадрат тендеуге келтірілген тендеулер жөніндегі білімдерін
тиянақтау, толықтыру бекіту

2)Оқушылардың іскерліктерін өз бетімен еңбектену сезімдерін білімдерін
дамыту.

3) Оқушыны шыдамдылыққа ұйымшылдыққа тәрбиелеу

Сабақтын түрі: қайталау білімдерін бекіту

Сабақтын көркемшілігі: слайд, логикалық есептер. Таратпа қағаз.

Сабақтын барысы:

І.Ұйымдастыру кезеңі. Оқушылармен амандасу,түгендеу,зейіндерін сабаққа
аудару;

ІІ."Миға шабуыл" қызығушылықты ояту кезеңі.

|№ |Берілген теңдеу |Жауабы |
|1 | [pic] |4;-4 |
|2 | 3[pic] |0;[pic] |
|3 | 2[pic] |2;2[pic] |
|4 |5[pic] |1;0,2 |
|5 |[pic] |-10;9 |

А) Үй тапсырмасын тексеру

Б)Сергіту сәті

Ойлап, тап анаграммаларды шешу. Әріптерді дүрыс орналастыру арқылы
математикалық терминнің атауын жазындар: роаблаап, цналриса, тавкдар.
Жауаптары: Парабола, рационал, квадрат.

II Ауызша сұрақтар

1) Квадрат тендеу дегеніміз не?

2) Толымсыз квадрат тендеу дегеніміз не?

3) Тендеу шешімінің қандай жағдайлары бар

4) Кез келген квадрат тендеудің түбірлерін табу үшін қандай формула
қолданады? X1/2= b+√d

2a

5)Квадрат тендеудің қанша түбірі болатынын қалай анықтауға болады?

6) Жаңа айнымалы енгізу әдісін қарастырудың қандай қажеті бар?

7) Квадрат тендеуге келтірілген тендеулерді жаңа айнымалы енгізу
әдісін шешу үшін қандай алгоритм қолданамыз?

III) Біліміңді тексер.(Оқулықпен жұмыс)

1) 194(2)

2) 196(4)

3) 199(4)

ІІІ."Қатені тап" тақтамен жұмыс.

|№ |Тапсырмалар |Дұрыс жауабы |
|1 |а[pic] |Теңдеудің екі түбірі бар|
|2 |а[pic] |Теңдеудің шешімі жоқ |
|3 |Келтірілген квадрат теңдеудің жалпы түрі |[pic] |
|4 |Квадрат теңдеудің түбірлерін табу |[pic] |
| |формуласы | |
|5 |a[pic], а[pic] түріндегі теңдеу |Толымсы квадрат теңдеу |

ІҮ."Білгенге маржан" берілген биквадрат теңдеулерді шешіңдер.

1.4n4-7n2+3=0;

2.x4-4x2-45=0;

3.t4-34t+225=0;

Ү тапсырма (Интерактивті тақтада тапсырма орындалады)

1-тапсырма

[pic], [pic]

[pic], [pic], [pic]

[pic],[pic], [pic]

Жауабы: 5;-5

2-тапсырма

[pic] /*27

[pic]

[pic]

[pic]

Жауабы:[pic]

3-тапсырма

(2[pic]6, (2[pic]

[pic]

2[pic]

2[pic], [pic]

Жауабы: [pic]

ҮІ.Деңгейлік тапсырмалар беру

|№ |А тобы |В тобы |С тобы |
|1 |[pic] |(3-2х[pic] [pic] |2[pic] |
|2 |[pic] |(2х-7[pic] |2[pic] |

ҮІІ.Үйге тапсырма беру №196(2,4,6)

Оқушыларды бағалау

Мұхит атындағы жалпы орта білім беретін мектебі

Сабақтың тақырыбы

[pic]

8-а сынып

Пән мұғалімі Ш Искакова

Сабақтың тақырыбы: Фалес теоремасы

Білімділік: Фалес теоремасының тұжырымдамасын білу, дәлелдей білу, дәлелдей
білу, алған білімді есеп шығаруда қолдана білу. Кесіндіні циркуль мен
сызғыштың көмегімен тең кесінділерге бөле білу.
Дамытушылық: Оқушылардың ой өрісін, жазу, есте сақтау, сызбамен жұмыс істеу
қабілеттерін, дағдыларын дамыту.
Тәрбиелік: Дәлдікке, ұқыптылыққа, іскерлікке баулу
Сабақтың түрі: Жаңа сабақты меңгерту
Сабақтың әдісі: түсіндіру, топтық жұмыс, практикалық.
Сабақтың барысы:
1. Ұйымдастыру кезеңі. (2 мин)
Амандасу, түгендеу. Оқушылардың назарын аударту.
2. Өткен сабақты қайталау. (13 мин)
Сыныпты екі топқа бөліп, бірінші топқа параллелограмм мен ромб, екінші
топқа тіктөртбұрыш пен квадраттың ұқсастықтары мен айырмашылықтарын венн
диаграммасында көрсетіп, қасиеттерін атау тапсырылады. Циркуль мен
сызғыштың көмегімен салу есептерін өткенбіз. Циркуль мен сызғышты
пайдаланып кесіндіні тең екі кесіндіге қалай бөлетін едік? Қалай салатынын
тақтада бір оқушы көрсетеді.

Ал енді кесіндіні циркульмен сызғышты пайдаланып үш, төрт, бес т.б.
кесінділерге қалай бөлуге болады? Бұл сұраққа жауап беру үшін ежелгі грек
математигі Фалес теоремасын қолданады екенбіз.

3.Фалес теоремасы

а) Тарихына тоқталу

Фалес Милетский грек ғалымдарының тұңғышы б.э.д. 625-547 жылдар шамасында
өмір сүрген. Бүгінгі өтетін теоремамыз кесіндіні циркуль мен сызғыштың
көмегімен тең бөліктерге бөлуге қолданылады. Фалес диаметр дөңгелекті қақ
бөлетінін, тең бүйірлі үшбұрыштың табанындағы бұрыштары тең болатынын,
вертикаль бұрыштардың теңдігін, үшбұрыштардың теңдігінің бірінші белгісін
алғаш дәлелдеген. Б.ж.с. бұрын 585 жылғы 28 майда болған күн тұтылу
құбылысын алдын ала, алты ай бұрын айтқан. Гректер дүниеде жеті-ақ адам
данышпан болып туады депойлаған, Фалес солардың біріншісі деп есептеген.

Фалеске берілген сұрақтардан

Фалеске берілген сұрақтардан мынандай жауаптар алыныпты.

1 “Бәрінен де жасы үлкен кім?” дегенге:

“Құдай, өйткені ол тумаған.

2“Бәрінен де не үлкен?” дегенге:

“Кеңістік, өйткені ол бүкіл Дүниені қамтиды”.

3 "Не нәрсе ең әсем?" дегенге:

"Дүние, өйткені әсемдіктің бәрі соның құрамында".

4 “Ең дана не?” дегенге: "Уақыт, ол бәрін тудырды, тағы да тудырады".

5 “Барлыққа ортақ не?” дегенге:

“Үміт. Қолында еш нәрсе жоқтарда да өмірге деген үміт болмай қалмайды”.

6 "Ең оңай не?" дегенде:

"Басқаларға ақыл айту, өйткені оны өзі орындамасаң да болады",

7 "Не нәрсе күшті" десе:

"Сөзсіздік, ол бәрін жеңеді" дейді,

.

ә) Фалес теоремасы.

Егер бұрыштың қабырғаларын қиятын параллель түзулер оның бір қабырғасында
тең кесінділер қиса, онда олар екінші қабырғасында да тең кесінділер қияды.

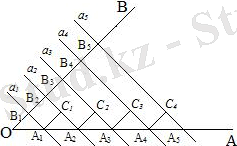Берілгені: <АОВ

а1 ІІ а2 ІІ а3 ІІ а4 ІІ а5 ІІ ...

а1 [pic] ОА=A1, а2 [pic] ОА=A2…

а1 [pic] ОB=B1 , а2 [pic] ОB=B2…

OA1=A1A2=A2A3=…

Д/к: ОВ1=B1B2=B2B3=…

Дәлелдеуі: A1C1II OB, A2C2 II OB, A3C3 II OB кесінділерін жүргіземіз.

Параллель түзулерді үшінші түзумен қиғандағы сәйкес бұрыштар
болғандықтан < C1A1A2=
ал шарт бойынша A1A2=A2A3=A3A4 онда үшбұрыштар бір қабырғасы және оған
іргелес екі бұрышы сәйкесінше тең болғандықтан ΔA1C1A2=ΔA2C2A3, ал
үшбұрыштардың теңдігінен А1С1=A2C2 болады. Сонда A1B1B2C1; A2B2B3C2
параллелограмм болады. Яғни А1С1=B1B2, A2C2=B2B3 немесе В1В2=B2B3

Қалған кесінділердің теңдігі де осылай дәлелденеді.

Ескерту: Бұрыштың қабырғаларының орнына кез келген екі түзуді алуға да
болады. Теореманың қорытындысы сол күйінде қала береді. Берілген екі түзуді
қиып өтетін және бір түзуден тең кесінділер қиып түсіретін параллель
түзулер екінші түзуден де тең кесінділер қиып түседі.

4. Фалес теоремасын практикада қолдануға есеп.

Есеп берілген АВ кесіндісін тең n белгілерге болу керек.

Шешуі:

1) АВ кесіндісін қамтитын түзуде жатпайтын А нүктесінен бастап а сәулесін
салам.

2) а сәулесінің бойына өзара тең АА1, А1А2, А2А3, …, Аn-1An кесінділерін
өлшеп саламыз.

3) АnB қосамыз

4) А1В1 ІІ А2В2 ІІ А3В3 ІІ AnВn түзулерін жүргіземіз

[pic] Фалес теоремасы бойынша АB1=B1B2=B2B3=…=Bn-1B

«Фалес» сөзжұмбағын шешу»

Сұрақтары:
1.Геометрия – ол геометриялық ... – лардың қасиеттері жөніндегі ғылым
2.Үшбұрыштың төбесін қарсы жатқан қабырғаның ортасымен қосатын кесінді?
3.Барлық қабырғалары тең үшбұрыш?
4.Бұрышты қақ бөлетін сәуле?
5.Бұрышты өлшейтін құрал?

|Ф | | | | | |
| | | | |А | | |

| | | | | | | | | |Л | | | | | | |Е | | | | | | | | | | | |С | | | | | | |
|

5. Сабақты бекіту, есеп шығару

Сыныпта №60 (1), №61 (1)

Берілген кесіндіні тең 3 бөлікке бөліңдер. Тақтада бір оқушы орындайды.
Қалғандары орнында орындайды.

1. Фалес теоремасының практикалық маңызы неде?

2. Фалес теоремасын дәлелдеу кезінде қандай теоремалар пайдаланылды?

6. Сабақты қорытындылау
7. Бағалау:
Бағасы:
Жалпы балл: 12
10-12 балл: «5»
7-9 балл: «4»
4-6 балл: «3»
0-3 балл: «2»

7. Үйге тапсырма §4. №60 (2), 61 (2)

.