Үшбұрыштар: негізгі теоремалар мен формулалар


Тлеулесова Жұмагүл Балташқызы
Астана қаласы,
Ә. Марғұлан атындағы №40 орта мектеп
Үшбұрыштар туралы теоремалар, олардың қасиеттері
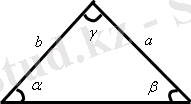
Үшбұрыштың бұрыштары
α 1 , β 1 , γ 1 - сыртқы бұрыштар
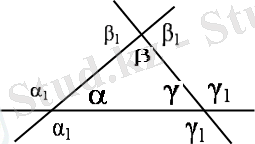 α, β, γ - ішкі бұрыштар
α, β, γ - ішкі бұрыштар
1) α + β + γ = 180 0
2) α 1 + β 1 + γ 1 = 360 0
3) α 1 = β + γ; β 1 = α + γ; γ 1 = α + β;
4) a + b › c; b + c › a; a + c › b;
5) a - b ‹ c; b - c ‹ a; a - c ‹ b;
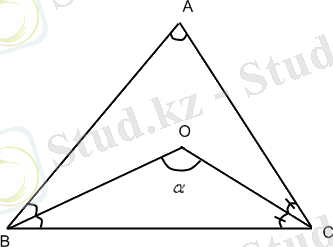
\[a=90^{0}-{\frac{A}{2}}\]
Биіктік
Үшбұрыштың төбесінен қарсы жатқан қабырғаны қамтитын түзуге түсірілген перпендикуляр.
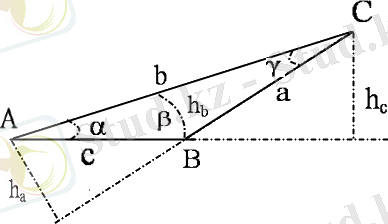 1) h
a
=
1) h
a
=
h b =
h c =
2) h a : h b : h c =
 3)
3)
r - іштей сызылған шеңбер радиусы.
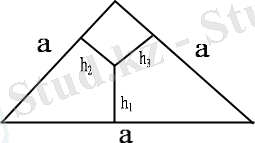
h 1 + h 2 + h 3 =
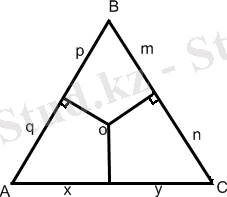
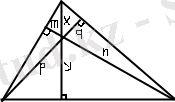 xy=pq=mn
xy=pq=mn
x 2 + n 2 + p 2 = y 2 + q 2 + m 2
Медиана
Үшбұрыштың төбесі мен қарсы жатқан қабырғаның ортасын қосатын кесінді.
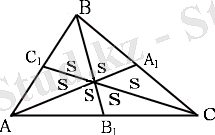 ВА
1
=СА
1
ВА
1
=СА
1
ВС 1 =АС 1
АВ 1 =СВ 1
- АА1= ma==;
BB 1 = m b =
\[\frac{1}{2}\sqrt{2(a^{2}+c^{2})-b^{2}}\]=\[\frac{1}{2}\sqrt{a^{2}+c^{2}+2a c{\cal C}o s\beta}\];CC 1 = m c =
\[\frac{1}{2}\sqrt{2(a^{2}+d^{2})-c^{2}}\]=\[\frac{1}{2}\sqrt{a^{2}+b^{2}+2a b C o s\gamma}\];
2)
m a 2 + m b 2 + m c 2 =
\[{\frac{3}{4}}{\Big(}a^{2}+b^{2}+c^{2}{\Big)}\];
3)
a =
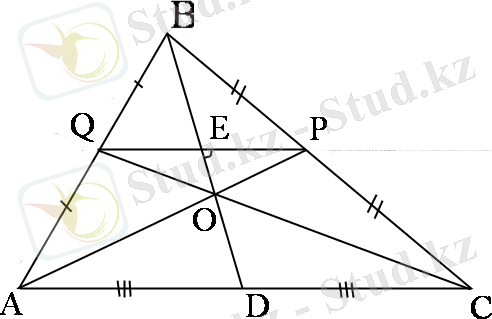 c =
c =
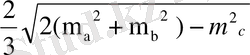
4)
A(x 1 ; y 1 ), B(x 2 ; y 2 ), C(x 3 ; y 3 )
O(x; y) x =
y =
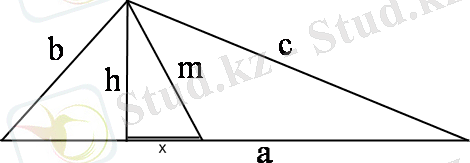
BD = m b , CQ = m c, AC = m a , OE =
S ∆EOP = S ∆EOQ =
S ∆BQE = S ∆BEP =
5) Бір төбеден шығатын биіктігі мен медианасының арасындағы кесінді:
x =
Биссектриса
Үшбұрыштың бұрышын қақ бөлетін сәуле.
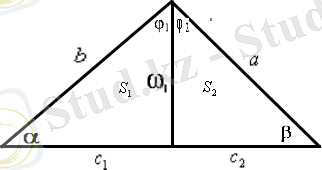
1)
2) ω α =
ω β =
ω φ =
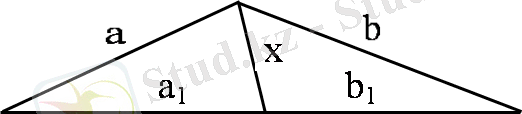
3)
x 2 = ab-a 1 b 1 , x - биссектриса;
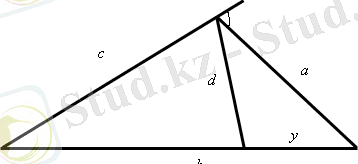
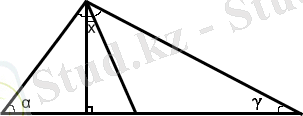
x =
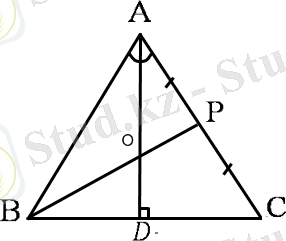
AC = BC, AP = PC,
Іштей және сырттай сызылған шеңбердің радиустары.
1) Үшбұрыштың биссектрисаларының қиылысу нүктесі іштей сызылған шеңбердің центрі болады.
2) Үшбұрыштың орта перпендикулярларының қиылысу нүктесі сырттай сызылған шеңбердің центрі болады.
 3) r =
3) r =
r - іштей сызылған шеңбердің радиусы;
4) R =
R - сырттай сызылған шеңбердің радиусы;
5) R =
6) r = (p-a) tg
Үшбұрыштың ауданы
- S =- биіктігі арқылы;
- S =- Герон формуласы;
- ==pr - іштей және сырттай сыз. шеңб. радиустары арқылы;
- S =m =- медиана арқылы;
- S =
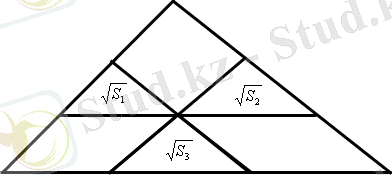
S = (
\[\sqrt{\mathrm{\stackrel{S}{B_{1}}}}\ +\sqrt{\mathrm{\stackrel{S}{B}}}\,+\sqrt{\mathrm{\stackrel{S}{B}}}_{3}\]) 2
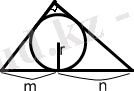
S = m n
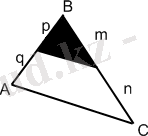
S 1 =
Үшбұрыштағы негізгі теоремалар
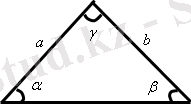 1. Синустар теоремасы:
1. Синустар теоремасы:
2. Косинустар теоремасы:
3. Мольвейде формуласы:
4. Тангенстер теоремасы:
5.
Жеке түрінде
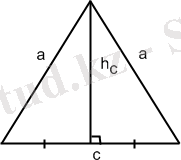 1. Тең бүйірлі үшбұрыш
1. Тең бүйірлі үшбұрыш
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz