Арифметикалық прогрессия: анықтама, n-ші мүшесінің формуласы және есептерді шығару

Скачать

Сабақтың тақырыбы: Арифметикалық прогрессия

Мақсаты: а) Арифметикалық прогрессияның анықтамасын меңгеріп, n-ші мүшесінің формуласын меңгеріп, есептер шығаруға қолдана білуге үйрету. АКТ-ны пайдаланып жаңа сабақ түсіндіру.

ә) Теориялық білімін практикада ұштастыра отырып, ойлау қабілеттерін, танымын, пәнге қызығушылығын арттыру, АКТ-ны пайдалануға баулу.

б) Оқушының белсенділігін арттыру, өз бетінше оқуға, ізденуге тәрбиелеу.

Күтілетін нәтиже: Арифметикалық прогрессияның тізбек екендігін, n-ші мүшесінің формуласын меңгеріп есептер шығара білу.

Түрі: дәстүрлі

Әдісі: сұрақ-жауап, есептер шығару, тест алу, деңгейлеп оқыту технологиясын қолдану.

Көрнекіліктері: интербелсенді тақта, ауызша есептеу, тест тапсырмалары, формулалар, топшамалар, т. б.

Сабақтың барысы:

I. Ұйымдастыру бөлімі

II. Үй тапсырмасын тексеру

III. Ой қозғау (арифметикалық прогрессия туралы айтқызу)

IV. Негізгі бөлім

V. Есептер шығару

а) Ауызша жаттығу

ә) Мысалдар шығару

б) Топшамамен жұмыс

VI. Оқулықпен жұмыс

VII. Кестемен жұмыс

VIII. Сергіту сәті

IX. Тест

X. Қорытынды

XI. Үй тапсырмасы

XII. Бағалау

II. Үй тапсырмасын тексеру

№165. 2, 4, 6, 8, 10, 12, 14, …

№167. 33, 35, 37, 53, 55, 57, 73, 75, 77 . . .

• Тізбек деген не?
• Шекті тізбек, шексіз тізбек деген не?
• Монотонды тізбектер деген не?
• Тізбектер қандай тәсілдермен беріледі?

III. Ой қозғау

Ежелгі замандардан бастап адамзат арифметикалық прогрессияның заңдылықтарын қолдана білген. Мәселен, Біздің заманымызға дейінгі ежелгі вавилондықтардың сына жазу (клинопись) кестелерінде, ежелгі мысырлық және гректердің папирустарында арифметикалық прогрессияға көптеген мысалдар кездеседі. Ежелгі грек ғалымдары прогрессиялардың кейбір қасиеттерін және олардың қосындысын таба білген.

Жалпы, арифметикалық прогрессия атауы сандардың арифметикалық ортасы (формуласы) ұғымынан ауысқан, ал геометриялық прогрессия атауы кесінділерінің геометриялық пропорционалдығынан (формуласы) ауысқан.

Арифметикалық прогрессия мүшелері қосындысының формуласын грек оқымыстысы Диофант (3ғ) дәлелдеген.

Арифметикалық прогрессиялар үшін жазылған формуласы формуласына байланысты атақты неміс математигі Карл Фредрих Гаусстың (1777-1855) өмірінен қызықты эпизод аңызға айналған. Мұғалім өзге сынып оқушыларының жұмыстарын тексеру мақсатында алдындағы оқушыларына 1-ден 40-қа дейінгі сандардың қосындысын табуды тапсырды. Бұл есепті 9 жасар Гаусс бір минутта шығарып, жауабын айтқан. Оның есепті шығару тәсілі мынадай еді:

1, 2, 3, . . . , 20

+

40, 39, 38, . . . , 21

41, 41, 41, . . . , 41

Мұндай парлар саны 20 болғандықтан, берілген қосынды 41*20=820-ға тең, Яғни Гаусс арифметикалық прогрессия заңдылықтарын қолданды.

IV. Негізгі бөлім

а ₁ =0, ал келесі мүшелері алдыңғы мүшесіне 2-ні қосқанда шығатын тізбекті жазайық: а ₁ =0, а ₂ =0+2=2, а ₃ =2+2=4, а ₄ =2+4=6, . . . Сонда а ₁ =0, а _n+1 =a _n +2.

Екінші мүшесінен бастап кез келген мүшесі өзінің алдыңғы мүшесіне тұрақты d санын қосқанда шығатын сандық тізбек арифметикалық прогрессия , ал

d саны - арифметикалық прогрессияның айырымы деп аталады.

Арифметикалық прогрессияның көршілес екі мүшесінің айырымы d санына тең:

а ₂ - а ₁ = а ₃ - а ₂ = а ₄ - а ₃ =…= а _n+1 - a _n =…=d.

1) а ₁ =а берілген сан, 2) а _n+1 =a _n + d шарттары берілсе, онда арифметикалық прогрессия анықталады.

Арифметикалық прогрессия айырымы оң сан болғанда - өспелі , ал теріс сан болғанда - кемімелі деп аталады.

Арифметикалық прогрессияның а ₁ мүшесі мен d айырымы берілсе:

а ₂ =a ₁ +d;

a ₃ = а ₂ +d=(a ₁ +d) +d= a ₁ +2d;

а ₄ = а ₃ +d=(a ₁ +2d) +d= a ₁ +3d;

a ₅ = а ₄ +d=(a ₁ +3d) +d= a ₁ +4d;

.

a _n =a _n-1 +d=a ₁ +(n-2) d+d= a ₁ +(n-1) d.

Сонымен,

a _n =a ₁ +(n-1) d - n-ші мүшесінің формуласы (1)

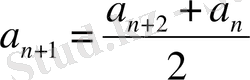Арифметикалық прогрессияның қатарлас үш мүшесінің ортаңғысы екі шеткі үш мүшелерінің арифметикалық орташасына тең.

1-мысал. а ₁ =3, 5 және d = 1, 5 болатын арифметикалық прогрессияның 100-мүшесін табайық:

а ₁₀₀ =3, 5+1, 5(100-1) =3, 5+148, 5=152.

Жауабы: 152

2-мысал. 6, 10, 14, . . . арифметикалық прогрессиясының кез келген мүшесін анықтайтын формуланы табайық.

Арифметикалық прогрессияның айырымы d=10-6=4, а ₁ =6 болатындықтан, (1) формуласы бойынша

a _n = а ₁ +(n-1) ^. d=6+(n-1) ^. 4=4n+2

Жауабы: a _n =4n+2

V. Есептер шығару

а) Ауызша жаттығу

Мысалы: а ₁ =5 d = 2 а ₂ =? Ж: 7

а ₁ =31 d = -5 а ₂ =? Ж: 26

а ₁ =1, 5 d = 3 а ₂ =? Ж: 4, 5

а ₁ =4 d = 1, 5 а ₂ =? Ж: 5, 5

ә) Мысалдар

1) 30, 45, 60, . . . d = ? Ж: 15

2) 160, 190, 210, . . . d = ? Ж: 30

3) 360, 240, 120, . . . d = ? Ж: -120

4) , , 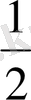, 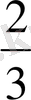. . . d = ? Ж:

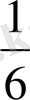
б) Топшамамен жұмыс

№1 топшама

Арифметикалық прогрессияның a ₁ =7, 2, d=3 болғанда а ₂ -і мүшесін тап.

№2 топшама

Арифметикалық прогрессияның a ₁ =6, 1, а ₂ =7, 1 болғанда, d-ны тап.

№3 топшама

3, 13, 23, 33, . . . тізбегі арифметикалық прогрессия бола ма?

№4 топшама

а ₁ , а ₂ , 20, 15, 10, … арифметикалық прогрессияның а ₁ ; а ₂ мүшелерін табыңдар.

№5 топшама

a ₁ =20, 3 d=-0, 4, n=30 арифметикалық прогрессияның a _n мүшелерін тап.

VI. Оқулықпен жұмыс

№193

1. а ₁ , а ₂ , 15, 20, 25, . . . 2. а ₁ , а ₂ , -20, -17, -14, ……

d = а ₄ - а ₃ = 20-15 = 5 d= а ₄ - а ₃ =- 17-(-20) =3

d = 5 d=3

а ₂ = а ₃ -d=15-5=10 а ₂ = а ₃ -d=-20-3=-23

a ₁ =a ₂ -d=10-5=5 a ₁ =a ₂ -d=-23-3=-26

Жауабы: a ₁ =5; а ₂ =10. Жауабы: a ₁ =-26; а ₂ =-23.

VII. Кестемен жұмыс

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс