11-сынып (жаратылыстану-математикалық бағыт): иррационал теңдеулер мен теңсіздіктерді және олардың жүйелерін шешу


11 сынып, жаратылыстану- математикалық бағыты.
Тақырыбы: Иррационал теңдеулерді, олардың жүйелерін және иррационал теңсіздіктерді шешу.
Сабақтың мақсаты:1. Иррационал теңдеулер мен олардың жүйелеріне арналған есептерді шешу дағдыларын жетілдіру, ҰБТ-де кездесетін иррационал теңдеулер мен теңсіздіктерді шешу.
2. Оқушылардың ақыл-ойын жан-жақты дамыту, математикалық сауаттылығын арттыру, теориялық білімдерін практика жүзінде қолдану дағдысын қалыптастыру.
3. Жауапкершілікке, өз бетімен жұмыс істеуге тәрбиелеу, пәнге қызығушылығын арттыру.
Сабақтың түрі: Бекіту сабағы
Сабақтың әдісі: Практикалық, сұрақ-жауап, өзіндік жұмыс, тест
тапсырмалары
Сабақтың көрнекілігі: интерактивті тақта, үлестірмелі карточкалар, жауап парақтары « Білім - біліктілікке жеткізер баспалдақ, ал біліктілік - сол білімді іске асыра білу дағдысы » Ахмет Байтұрсынов
Сабақтың барысы: І. Ұйымдастыру.
а) Оқушылармен амандасу, сабаққа дайындығын тексеру және
оларды түгендеу.
ІІ. Теориялық білімдерін тексеру. Сұрақ- жауап арқылы.
1. Иррационал теңдеу деп қандай теңдеуді айтамыз?
2. Иррационал теңдеулерді шешудің жалпы әдістері қандай?(Жауабы 1), 2), жаңа айнымалы еңгізу тәсілі, айнымалының табылған мәндерін міндетті түрде тексеру)
3. Бөгде түбір дегеніміз не?( Теңдеуді қанағаттандырмайтын айнымалының кейбір мәндерін бөгде түбірі болады)
4. Иррационал теңдеулер жүйесі дегеніміз не?
5. Иррационал теңдеулер жүйесі шешуде қандай тәсілдерді қолдану керек?
6. Иррационал теңсіздік деп қандай теңсіздікті айтамыз?
7. ииррационал теңсіздіктерді шешу үшін қолданылатын қатынастарды қайталайық. III . Ауызша есептеу : 1. Өрнектің мәнін есептеңдер: а) ( ) ә) 3 √ 8* 343*125;
Теңдеулерді шешіңдер:
2.
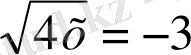 ; 3.
; 3.
 4.
4.
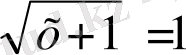
5.
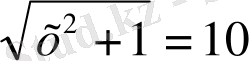 6.
6.
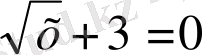 7.
7.
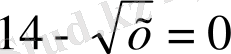 8.
8.
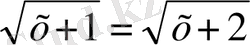 .
.
Бағалау: Әрбір дұрыс жауап 1балл. Жауаптары: 1. а) 1, 2 ә) 70
2. Жауабы жоқ, 3) . 162 4) . 0 5) -3, +3 6. Жауабы жоқ. 7) . 196 8) Жауабы жоқ.
IV. Деңгейлік есептер шығару.
А деңгейі : 1 . √27+ √х - 2 = √75; 2 . х - √х - 6 ═ 0;
Бағалау:Әрбір дұрыс жауап 1балл.
В деңгейі: 3. √ 15 - х + √3 - х ═ 6; 4 . 3√х + 2√у = 23,
10√х - 7√у = 22.
Бағалау: Әрбір дұрыс жауап 2 балл.
С деңгейі: 5 . √х + √у = 5, 6 . √х 2 - 2х - 8 ≤ х.
х + у + 4√ху =37.
Бағалау:Әрбір дұрыс жауап 3 балл.
Қосымша тапсырма : х -тің қандай мәнінде мына у ═ 10 + х - √2-х функциясы оң мән қабылдайды?
Бағалау:Дұрыс жауабына 3 балл.
Жауаптары: 1. х=14; 2. х=9; 3. х=-1; 4. (25, 16) ; 5. (4; 9), (9; 4) ;
6. х ; Қосымша тапсырманың жауабы: х (-1; 2] .
V. Тест :
1. Есепте:0, 1√400 +2, 1*√
А) 20, 9 В) 27 С) 2, 7 Д) 20, 7 Е) 0, 9
2. +
А) 28 В) 44 С) 36, 125 Д) - 10 Е) 35, 875.
3. Теңдеуді шішініз: 2
А) - В) С) түбірі жоқ Д) - , Е) .
4. Теңсіздікті шішініз:
А) (5; 8) U (8; ) В) (- ) U(5; ) С) (- ) U( ) Д) ( ) Е) (5; 8) .
5. 8 санының оң жағына да сол жағына да өзінен басқа бір санды жаздық. Шыққан сан 6-ға бөлінеді. Біз қандай сады жаздық?
А) 1 В) 2 С) 5 Д) 4 Е) 3
Бағалау: Әрбір дұрыс жауап 1балл.
Бағалау парағы:
25 балдан жоғары - «5»
15-24 балл - «4»
8 - 14 балл - «3»
VI. Қорытындылау.
VII. ҮЙ ТАПСЫРМАСЫ: 1. Х + = теңдеуін шішініз(ҰБТ-де кездескен есеп)
2. 2011 жылғы Азиадада қазақстандық команда 53- алтын мен күміс, 49- қола мен алтын және 38- күміс пен қола медаль женіп алды. Барлығы неше медаль женіп алды?
А) 38 В) 53 С) 70 Д) 110 Е) 140
VIII. Бағалау парақтарынды тапсырындар.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz