Иррационал теңдеулер мен жүйелері: түбір таңбасының астындағы шешу алгоритмі


Сабақтың тақырыбы: Иррационал теңдеулер және олардың жүйелерін шешу
Сілтеме: А. Әбілқасымова. Алгебра және анализ бастамалары 11сынып
Сабақтың мақсаты:
- Білімділік:Оқушыларды иррационал теңдеу және иррационал теңдеулер жүйесімен таныстыру. Иррационал теңдеулер мен олардың жүйесін шешуді үйрету.
- Дамытушылық:Деңгейлік тапсырмаларды әр оқушының қабілеті жеткенше біртіндеп орындауға жетелеу арқылы, оның дамуына жағдай жасау.
- Тәрбиелік:Оқушыларды өз бетінше жұмыс жасауға, қорытынды шығаруға, ізденуге дағдыландыру.
Сабақтың түрі: Дәстүрлі сабақ
Сабақтың типі: Жаңа білімді игеру және оны алғашқы бекіту сабағы.
Сабақтың көрнекілігі: Интерактивті тақта, слайдттар, тірек сызбалар, түсіндірмелер.
Сабақтың әдісі: Түсіндірмелі-иллстративтік, өз бетімен жұмыс.
Сабақтың барысы.
І. Ұйымдастыру кезеңі
Оқушылардың сабаққа қатысуы мен дайындығын тексеру
ІІ. Үй тапсырмасын тексеру №112, 114
ІІІ Жаңа сабақ
- Қайталау оқу анасы. (сәйкесін тап) Оқушылардың тірек білімдерін жүйелеу
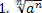
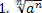 =
=
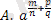
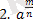
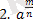 =
=
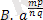
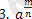
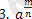 *
*
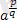
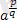 =
=
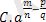
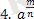
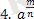 :
:
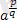
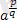 =
=
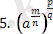
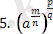 =
=
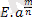
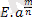 *
*
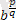
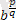
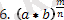
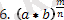 =
=
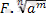
Жауаптары :1-D, 2-F, 3-A, 4-C, 5-B, 6-E.
- Жаңа сабаққа дайындық.
Теңдеу дегеніміз не?
Оң жақ және сол жақ бөлімдері құрамында x айнымалысы бар алгебралық өрнектер.
- Білімдіге биіктен орын
Жаңа сабақты түсіндіру
Анықтама. Иррационал теңдеу деп айнымалысы түбір таңбасының ішінде , сонымен қатар бөлшек көрсеткішті дәреженің негізі болатын теңдеуді атаймыз.
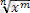
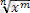 =b
=b
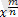
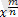 =b
=b
Мысалдар:
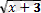
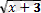 =2x-1;
=2x-1;

 -12
-12
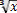
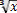 =3;
=3;
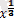
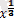 -5=0;
-5=0;
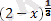
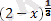 =
=
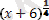
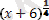 +7x
+7x
Иррационал теңдеуді шешудің жалпы әдісі
- Егер иррационал теңдеуде бір ғана түбір белгілі болса, онда түбір белгісі теңдеудің бір жақ бөлігінде қалатын етіп түрлендіреміз. Одан кейін теңдеудің екі жақ бөлігін де бірдей дәрежеге шығару арқылы рационал теңдеу аламыз;
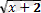
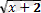 =x;
=x;
x+2=x 2 ;
x 2 -x-2=0;
x 1 =2; x 2 =-1
- Егер иррационал теңдеуде екі немесе одан да көп түбір белгісі болса, онда алдымен түбірдің біреуін теңдеудің бір жақ бөлігінде қалдырып, теңдеудің екі жақ бөлігін бірдей дәрежеге шығарамыз. Содан кейін рационал теңдеу алынғанша осы тәсілді қайталаймыз
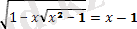
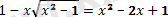
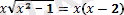
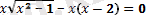
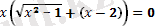
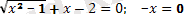

 бөгде түбір
бөгде түбір
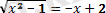
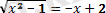
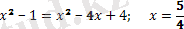
- Анықтама. Құрамында иррационал теңдеуі бар жүйені иррационал теңдеулер жүйесі деп атайды.
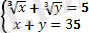
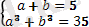
немесе
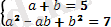
a=2; b=3; және
a=3; b=2
х=8, y=27;
x=27, y=8;
IV Ой толғаныс
Оқулықпен жұмыс
А-деңгейі №120, В-деңгейі №125, С-деңгейі №132
Сабақты қорытындылау
Тақырып соңындағы сұрақтарға жауап алу
V Оқушыларды бағалау
Бағалау парағы бойынша оқушыларды бағалау
VІ Үй тапсырмасы №121, №126
Жәлиев Сағдат Базарбайұлы
№264 мектеп-лицей, Қызылорда қаласы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz