Ұлттық бірыңгай тестіге арналған математикалық есептердің шығару жолдары


Ұлттық бірыңгай тестінде берілетін кейбір есептердің шығару жолдары.
Әлемдік білім кеңістігіне шығуда техникалық бағыттағы ғылым салаларын дамыту міндеті тұр. Ол үшін бұл бағытта, әсіресе математиканың оқыту сапасын көтеру кезек күттірмейтін міндет болып табылады.
Оқушылардың математикадан терең білімді болуы- өз білімін үнемі жетілдіріп, оқушылармен жұмыста деңгейлеп оқыту технологиясын жете меңгерген ұстазға тікелей байланысты. Осы орайда мен сіздерге бірнеше есептердің шығарылу жолдарын ұсынып отырмын .
1-есеп. (2014. 1-нұсқа 17 есеп) .
Теңбүйірлі трапецияның бүйір қабырғасы , ал табандары 3 пен 4 болса, диагоналін табыңдар.
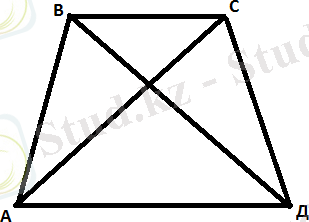 Берілгені: АВ=СД=
. ВС=3. АД=4
Берілгені: АВ=СД=
. ВС=3. АД=4
Табу керек: АС диагоналының ұзындығы.
Шешуі: Птолемей теоремасы: Шеңберге іштей сызылған төртбұрыштың диагоналдарының көбейтіндісі, оның қарама -қарсы жатқан қабырғаларының көбейтінділерінің қосындысына тең.
Олай болса АС·ВД=ВС·АД+АВ·СД
АС 2 =3·4+ АС=5
Ескерту: Теңбүйірлі трапецияға сырттай шеңбер сызуға болады.
2-есеп. (2014. 2-нұсқа 17 есеп)
Трапецияның бір табаны биіктігінен 3 см артық, ал екінші табаны биіктігінен 3 см қысқа. Егер трапецияның ауданы 100 см 2 болса, оның табандарын табыңдар.
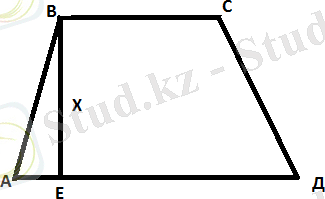 Берілгені: S=100 см
2
, ВЕ= х, АД= х+3, ВС= х-3
Берілгені: S=100 см
2
, ВЕ= х, АД= х+3, ВС= х-3
Табу керек: ВС, АД
Шешуі: Трапецияның ауданы
S= формуласымен табылады. Онда 100=
х 2 =100, х =±10
Ұзындықтың теріс санмен өрнектелмейтіндігін ескеріп х=ВЕ=10 см. Олай болса ВС=7 см, АД=13 см.
3-есеп. (2014. 3-нұсқа 11 есеп)
Теңдеулер жүйесін шешіңдер.
Шешуі: Теңдеулер жүйесін шешудің алгебралық қосу тәсілін пайдаланып аламыз.
х
У айнымалысын табу үшін жүйенің бірінші теңдігінен у
Жауабы: х=2. у= -2. 5
4-есеп. (2014. 3-нұсқа 17 есеп) .
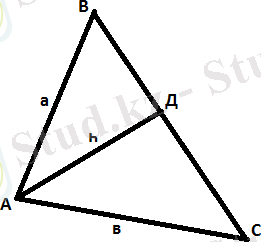 Үшбұрыштың қабырғалары а және в, үшінші қабырғаға түсірілген биіктік һ болса, сырттай сызылған шеңбердің радиусын табыңдар.
Үшбұрыштың қабырғалары а және в, үшінші қабырғаға түсірілген биіктік һ болса, сырттай сызылған шеңбердің радиусын табыңдар.
Шешуі: Синустар теоремасын қолданамыз.
АДС-дан sin C=
2R= = = , R=
Жауабы: R=
5-есеп. (2014. 3-нұсқа 25 есеп) .
MNPQ қабырғасы 6 см-ге тең квадрат . А мен В квадратты қақ бөлетін түзу бойында орналасқан . Нүктелер MAP және MBP сынығы квадратты аудандары бірдей 3 бөлікке бөледі. АВ -ның ұзындығын табыңыз.
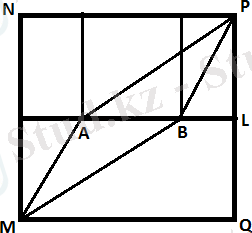 Берілгені: S
кв
=36 см
2
Берілгені: S
кв
=36 см
2
Табу керек: АВ кесіндісінің ұзындығы.
Шешуі: MAP және MBP сынықтары квадратты аудандары бірдей 3 бөлікке бөлетін болса, әр бөліктің ауданы төмендегідей болады.
36/3=12
S MAPB =12 см 2 және S APB = S MAB =6 см 2
S APB = мұнда PL = 6/2=3 Берілгендерді орнына қойып AB= 4 см табамыз.
Жауабы: AB= 4 см.
6-есеп. (2014. 4-нұсқа 8 есеп) .
Үшбұрыштың үш қабырғасы 21 см, 28 см, 35 см. Үшбұрыштың түрін анықтаңыз.
Шешуі:
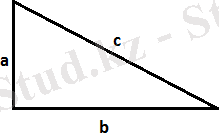
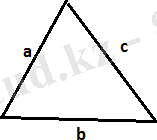
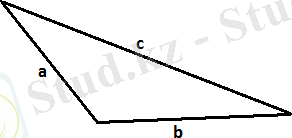
Үшбұрышта үлкен қабырғаға үлкен бұрыш жататындықтан с қабырға үшін, егер
c 2 =a 2 +b 2 теңдігі орындалса онда үшбұрыш тікбұрышты болады,
c 2 a 2 +b 2 теңсіздігі орындалса онда үшбұрыш доғалбұрышты болады,
c 2 a 2 +b 2 теңсіздігі орындалса онда үшбұрыш сүйірбұрышты болады.
Біздің мысалымызда 35 2 =21 2 +28 2 теңдігі орындалады. Олай болса берілген үшбұрыш тікбұрышты.
Жауабы: үшбұрыш тікбұрышты.
7-есеп. (2013. 1-нұсқа 20 есеп) .
Теңсіздікті шешіңіз: 2 sin 2 x-7 sin x-4 0
 Шешуі:
sin x= а белгілеуін енгізіп мынадай квадрат теңдеу аламыз. 2а
2
-7а-4 =0 оны шешімдері а
1
=-
, а
2
=4 болып табылады. Көбейткіштерге жіктеп берілген теңсіздікті төмендегідей теңсіздікті шешуге келтіреміз.
Шешуі:
sin x= а белгілеуін енгізіп мынадай квадрат теңдеу аламыз. 2а
2
-7а-4 =0 оны шешімдері а
1
=-
, а
2
=4 болып табылады. Көбейткіштерге жіктеп берілген теңсіздікті төмендегідей теңсіздікті шешуге келтіреміз.
(2 sin x +1) ( sin x -4) 0 мұнда, - sin x 1 болатынын ескерсек (осы жағдайды оқушылардың қөбі ескере бермейді, сондықтан теңсіздікті шешуде кедергілерге кездеседі. ) sin x -4 теңсіздігі орынды, олай болса 2 sin x +1 немесе sin x теңсіздігнің шешімі [- ] . Бұл берілген теңсіздіктің шешімі болып табылады.
8-есеп. (2014. 5-нұсқа 17 есеп) .
АВС үшбұрышында А=60 0 . =75 0 , болса қатынасын табыңыз.
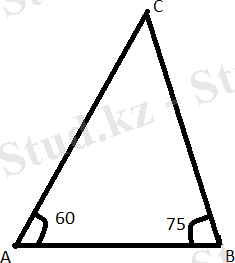 Шешуі:
Үшбұрыштың үшінші бұрышын тауып аламыз.
Шешуі:
Үшбұрыштың үшінші бұрышын тауып аламыз.
С = 180 0 -(60 0 +75 0 ) = 45 0
Синустар теоремасын пайдаланып
Теңдеуді түрлендіріп
Жауабы:
9-есеп. (2013. 3-нұсқа 19 есеп) .
Егер .
 Шешуі:
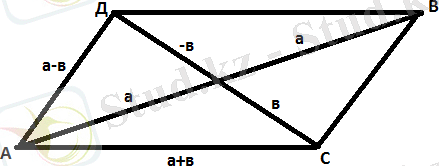
Мұндай есептерді шығаруда параллелограмм ережесін пайдаланган тиімді.
АВС үшін АВ қабырғасына жүргізілген медианаға
Шешуі:
Мұндай есептерді шығаруда параллелограмм ережесін пайдаланган тиімді.
АВС үшін АВ қабырғасына жүргізілген медианаға
m AB 2 = қасиет тән.
Онда берілгендерді пайдаланып 10 2 = аламыз. Теңдеуді түрлендіріп а 2 =225. a=15
Жауабы: a=15
10-есеп. (Математика Есеп жинақ. авторы Қиябаева. З. Н)
Кестенің көмегінсіз есепте. tg 20 0 tg 40 0 tg 60 0 tg 80 0
Шешуі. Есеп шығаруға мына қолайлы формуланы қолданамыз.
tg a tg(60 0 -a) tg(60 0 +a) = tg 3a
олай болса, tg 20 0 tg 40 0 tg 60 0 tg 80 0 = tg 20 0 tg (60 0 -20 0 ) tg (60 0 +20 0 ) = tg (3·20 0 ) = tg 60 0 = =3
Жауабы 3
Жоғарыда көрсетілген формуланы синус және косинус функциялары үшін беремін.
sin a sin (60 0 -a) sin (60 0 +a) = sin 3a
cos a cos (60 0 -a) cos (60 0 +a) = cos 3a
11-есеп . (Математика Есеп жинақ. авторы Қиябаева. З. Н)
Теңсіздікті шешіңдер.
Шешуі: 1-тәсіл . (Логарифмнің негізін екі жағдайда қарастыру. )
1-жағдай негізіндегі х 0 х 1 және х 1 болғанда, қарастырайық,
(0:1)
(2, 5:5)
Жауабы: (0:1) ᴜ (2, 5:5)
2-тәсіл. (Логарифмдік теңсіздікті оған мәндес рационал теңсіздіктер жүйесімен алмастыру. )
$\left\{ \begin{array}{r} `(х - 1) \bullet (5 - х - х) < 0 \\ \binom{х > 0}{х \neq 1} \\ 5 - х > 0 \end{array} \right. \ $
Бұл теңсіздіктердің біріншісін интервалдар әдісімен шешейік.
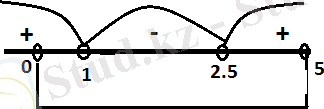 Жауабы: (0:1) ᴜ (2, 5:5)
Жауабы: (0:1) ᴜ (2, 5:5)
Негізі айнымалы болып келетін логарифмдік теңсіздіктерді шешкенде көп жағдайда төмендегі формуланы пайдаланган тиімді. (стандарт емес әдіс)
$\Leftrightarrow \left\{ \begin{array}{r} `(һ(х) - 1) \bullet (f(х) - g(х) ) < 0 \\ \binom{һ(х) > 0}{һ(х) \neq 1} \\ \binom{f(х) > 0}{g(х) > 0} \end{array} \right. \ $
12-есеп . (Математика Есеп жинақ. авторы Қиябаева. З. Н)
Көрсеткіштік теңсіздікті шешіңдер.
Шешуі: 1-әдіс (стандартты емес әдіс)
=(х-2) 0 деп алып түрлендіреміз:( -1) ( -0
(х-3) (х-2) (х-4) теңсіздігін интервалдар әдісімен шешсек,

Жауабы: х (2:3) ᴜ (4: )
теңсіздігін төмендегі формула арқылы рационал теңсіздікке келтіруге болады. ( ) ( ) 0
Бұл әдіс уақытты үнемдеуге мүмкіндік береді.
2-әдіс. (оқулықтағы стандартты әдіс, яғни, негізін 1-ден артық және 1-ден кіші деп екі жағдайды қарастырып барып шешеді. )
(х-2) 0
1-жағдай: х-2 болғанда,
2-жағдай: 0 ,
Екі аралықты біріқтірсек, х (2:3) ᴜ (4: )
13-есеп. (Математика Есеп жинақ. авторы Қиябаева. З. Н)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz