Виет теоремасы туралы

Алгебра-8 Мерзімі: 5.12.2015ж.

Сабақтың тақырыбы: Виет теоремасы.

Сабақтың мақсаты: Оқушылардың Виет теоремасын және оған кері теореманы есеп шығаруда қолдана білуге дағдыландыру.

Сабақтың міндеттері:1. Виет теоремасын қолданып есеп шығару дағдысын қалыптастыру, алған білімдерін практикалық іс-әрекетте қолдана білуге үйрету.
2. Оқушылардың ойлау дағдысын қалыптастыра отырып,есте сақтауын, танымын, пәнге деген қызығушылығын, шығармашылықпен жұмыс істеу дағдыларын дамыту.
3. Есеп шешімін іздеу арқылы қиыншылықты жеңуге, дербестікке, тиянақтылыққа және нақтылыққа тәрбиелеу.

Сабақтың өту әдісі: Деңгейлеп, саралап оқыту.

Сабақтың түрі: Біліктілік пен дағдыны игеру және қалыптастыру сабағы.

Сабақтың көрнекілігі: Слайд, флипчарттар

Сабақтың құрылымы:
І. Ұйымдастыру кезеңі. Сабақтың мақсатын беру 1 мин
ІІ. Үй тапсырмасын тексеру. 555
Бірінші деңгей - танымдық деңгей (ауызша сұрақтар) 5 мин
ІІІ. Сергіту сәті 5 мин
ІҮ. Екінші деңгей - алгоритмдік деңгей
<<Зерде>> ойыны. Мақалдардың жалғасын тап. 5 мин
Ү. Флипчарт. Кесте толтыру. 8 мин
ҮІ Үшінші деңгей - эвристикалық деңгей. Әр есептің жауабын таңдау.
ҮІІ. Флипчарт. Виет теоремасына кері теореманы қолдану. 6 мин
Түбірлері 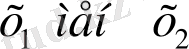болатын теңдеулерді жазыңдар:
ҮІІІ. Төртінші деңгей - шығармашылық деңгей. 10 мин
ІХ Квадрат теңдеудің түрлерін анықтау 2 мин
Х. Сабақты қорытындылау.
Квадрат теңдеуді шешудің әр түрлі әдістеріне тоқталу. 2 мин
ХІ. Оқушылар білімін бағалау.
Үйге тапсырма беру: № 297,299 1 мин

Сабақтың барысы:
І. Ұйымдастыру кезеңі. Сабақтың мақсатын беру
ІІ. Үй тапсырмасын тексеру.
Бірінші деңгей - танымдық деңгей (ауызша сұрақтар)
oo Квадрат теңдеудің анықтамасын кім айтады?
oo Қандай теңдеулер толымсыз квадрат теңдеулер деп аталады?
oo Дискриминантты табудың үш жағдайы
oo Квадрат теңдеулерді шешудің формуласы қалай жазылады?
oo Келтірілген квадрат теңдеу деп қандай теңдеуді айтамыз?
oo Виет теоремасы қалай жазылады?
oo Виет теоремасына кері теорема
ІІІ. Сергіту сәті

Жауабы: 1) З(2;5) 2) А(-5;3) 3) С(-6:-4) 4) А( -5;7)

ІҮ. Екінші деңгей - алгоритмдік деңгей
<<Зерде>> ойыны. Мақалдардың жалғасын тап.
А) х2 - 8х + 7 = 0 х1 + х2 = 8, х1х2 = 7 х1 = 1, х2 = 7
Жеті рет өлшеп, ( бір рет кес)
Ә) х2 - 11х + 10 = 0 х1 + х2 = 11, х1х2 = 10 х1 = 1, х2 = 10
Бір тал кессең, ( он тал ек)
Б) х2 - 9х + 8 = 0 х1 + х2 = 9, х1х2 = 8 х1 = 1, х2 = 8
Жігіт бір сырлы, ( сегіз қырлы)
В) х2 - 70х + 1200 = 0 х1 + х2 = 70, х1х2 = 1200 х1 = 30, х2 = 40
Ұлға 30 үйден, (қызға 40 үйден) тыю.

Ү. Флипчарт. Кесте толтыру.Келтірілген квадраттық теңдеудің түбірлерін, түбірлерінің қосындысы мен көбейтіндісінің мәндерін табыңдар және жауаптарын кестеге толтырыңдар.
Теңдеулер
х1+ х2
х1 · х2
Түбірлер
х1 және х2
х[2] - 2х - 3 = 0
-1+3=2
-1*3=-3
-1:3
Х2 + 5х - 6 = 0
-6+1=-5
-6*1=-6
-6:1
х[2] - х - 2 = 0
-1+2=1
-1*2=-2
-1:2
х[2]+ 7х + 12 = 0
-4+ (-3)=-7
-4* (-3)=12
-4:-3
ҮІ. Үшінші деңгей - эвристикалық деңгей. Әр есептің жауабын таңдау.
oo А) х2 - 2х - 35 = 0 1) х1 = 1, х2 = 7
oo Ә) х2 + 4х + 3 = 0 2) х1 = -11, х2 = 1
oo Б) х2 - 8х + 7 = 0 3) х1 = -1, х2 = -3
oo В) х2 + 10х - 11 = 0 4) х1 = -5, х2 = 7

ҮІІ. Флипчарт. Виет теоремасына кері теореманы қолдану.
Түбірлері 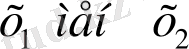болатын теңдеулерді жазыңдар:

Түбірлері
Қосындысы
Көбейтіндісі
Теңдеу
X1=-2 X2=3
-2+3=1
-2*3=-6
х2 -х - 6 = 0
X1=-5 X2=6
-5+6=1
-5*6=-30
х2 -х - 30 = 0
X1=-4 X2=-3
-4+(-3)=-7
-4*(-3)=12
х2 + 7х +12 = 0
X1=1,5 X2=4
1,5+4=5,5
1,5*4=6
Х2 -5,5х - +6 = 0

ҮІІІ Төртінші деңгей - шығармашылық деңгей.
1) а) 2х ( 5х - 7) = 2х2 - 5 ә) ( х + 4) 2 = 4х2 + 5
2) а) 5х2 + 4х - 1 = 0 ә) -23х2 - 22х + 1 = 0

Жауабы: 1) а) х1=5/4, х2=1/2 ә) х1=11/3, х2=-1
2) а) х1=1/5, х2=-1 ә) х1=1/23, х2=-1

ІХ.Квадрат теңдеудің түрлерін анықтау

Х.Сабақты қорытындылау.
Квадрат теңдеуді шешудің әр түрлі әдістеріне тоқталу.

ХІ. Оқушылар білімін бағалау. Үйге тапсырма беру: № 297,299