Тікбұрышты үшбұрыш салу

Сабақ: «Тікбұрышты үшбұрыш салу»

Мектеп: Подхоз ЖББНМ

Сабақ:«Тікбұрышты үшбұрыш салу»: Күні: 26. 01. 2016ж

Мектеп:Подхоз ЖББНМ: Аты-жөні: Мухтарова Айтканым Булатовна

Сабақ:«Тікбұрышты үшбұрыш салу»: Сынып: 8

Мектеп:Подхоз ЖББНМ: Қатысқан оқушы саны

Қатыспағандар

Сабақ:«Тікбұрышты үшбұрыш салу»: Сабаққа негізделген оқу мақсаттары:

Мектеп:Подхоз ЖББНМ: Тікбұрышты үшбұрышты сала білуге үйрену

Сабақ:«Тікбұрышты үшбұрыш салу»: Сабақ мақсаттары:

Мектеп:Подхоз ЖББНМ: Барлық оқушылар

Сабақ:«Тікбұрышты үшбұрыш салу»: А. Тікбұрышты үшбұрыштың анықтамасын біледі

Сабақ:«Тікбұрышты үшбұрыш салу»: Оқушылардың басым бөлігі

Сабақ:«Тікбұрышты үшбұрыш салу»: В. Тригонометриялық өрнетерді ажырата алады

Сабақ:«Тікбұрышты үшбұрыш салу»: Кейбір оқушылар :

Сабақ:«Тікбұрышты үшбұрыш салу»: С. Тікбұрышты үшбұрыштарды салу алгоритмін қолданып есеп шығара алады

Сабақ:«Тікбұрышты үшбұрыш салу»: Тілдік мақсат

Мектеп:Подхоз ЖББНМ: Оқушылар

Сабақ:«Тікбұрышты үшбұрыш салу»: Тікбұрышты үшбұрыщтың, тригонометриялық өрнектердің анықтамасын береді

Сабақ:«Тікбұрышты үшбұрыш салу»: Негізгі сөздер мен тіркестер

Сабақ:«Тікбұрышты үшбұрыш салу»: Даптермен, оқулықпен жұмыс

Сабақ:«Тікбұрышты үшбұрыш салу»: Сыныптағы диалог/жазылым үшін пайдалы тілдік бірліктер:

Сабақ:«Тікбұрышты үшбұрыш салу»: Талқылауға арналған тармақтар (тыңдалым)

Сабақ:«Тікбұрышты үшбұрыш салу»: Тікбұрышты үшбұрыш дегеніміз

Сабақ:«Тікбұрышты үшбұрыш салу»: Сіз неліктен екенін айта аласыз ба? (айтылым)

Сабақ:«Тікбұрышты үшбұрыш салу»:

Сабақ:«Тікбұрышты үшбұрыш салу»: Жазылым бойынша ұсыныстар

Сабақ:«Тікбұрышты үшбұрыш салу»:

Сабақ:«Тікбұрышты үшбұрыш салу»: Алдыңғы оқу

Мектеп:Подхоз ЖББНМ: «Негізгі тригонометриялық тепе-теңдіктер» және «Үшбұрыштарды шешу» салыстыра отырып айту

Сабақ:«Тікбұрышты үшбұрыш салу»: Жоспар

Мектеп:Подхоз ЖББНМ:

Сабақ:«Тікбұрышты үшбұрыш салу»: Жоспарланған уақыт

Мектеп:Подхоз ЖББНМ: Жоспарланған жаттығулар (төменде жоспарланған жаттығулармен қатар, ескертпелерді жазыңыз)

Формативті бағалау (ОҮБ)

Ресурстар

Сабақ:«Тікбұрышты үшбұрыш салу»: Басталуы

Мектеп:Подхоз ЖББНМ:

Кіріспе. Таныстырылым

(1-2 мин)

Ұйымдастыру

Үй тапсырмасын тексеру

Жаңа сабақтың табыс критериийін бірге анықтау.

Сабақ:«Тікбұрышты үшбұрыш салу»: Үй тапсырмасын тексеру (5мин)

Мектеп:Подхоз ЖББНМ:

Әр оқушы жеке тапсырмалар бойынша үй тапсырмасына жауап береді.

1) Кеспе қағаздар арқылы сұрау

а) Пифагор теоремасы

ә) Бұрыштың синусы

б) Бұрыштың косинусы

в) Бұрыштың тангенісі

д) Негізгі тригонометриялық теңбе-теңдік

2) Ауызша есеептер

3 ) Үй тапсырмасын өзара дәптерлерін ауыстыру арқылы тексеру.

Оқушылар бірін-бірі бағалайды

маркерлер, кесте, ноутбук, бағалау парақшалар, стикерлер

Сабақ:«Тікбұрышты үшбұрыш салу»: Ортасы

Мектеп:Подхоз ЖББНМ:

«Бірік, ойлан, бөліс»стратегиясы бойынша тақырыпты еске түсіру. Ресурс бойынша талдау

Мысалы. Сүйір бұрышының косинусы 3:5 қатынасына тең болатын үшбұрышты салайық.

Шешуі: Ізделінді тікбұрышты үшбұрыш АВС болсын, мұндағы АВ=c-гипотенуза; <С=90 ⁰ ; <A=α, BC=a, CA=b-катеттер.

cosα= 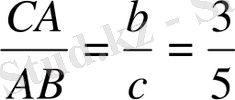теңдігі орындалу керек. Бірлік кесінді е таңдап аламыз. 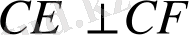сәулелерін жүргіземіз. 29 -сурет.

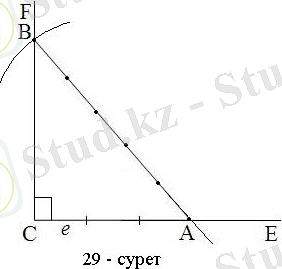
СЕ сәулесіне СА=3е кесіндісін өлшеп саламыз. Центрі А нүктесі етіп, АВ=5a кесіндісіне тең радиус етіп шеңбер жүргіземіз. Ол CF сәулесін В нүктесінде қиып өтеді. Нәтижесінде АВС тікбұрышты үшбұрышы салынады. Ол тікбұрышты үшбұрышта

cosα= 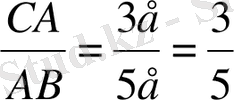болады. Демек, салынған үшбұрыш есептің шартын қанағаттандырады.

Есептер шығарады

№118, 120, 123

Екі жұлдыз, бір ұсыныс

Критерий бойынша бағалау

маркерлер, кесте, бағалау парақшалар, стикерлер

Сабақ:«Тікбұрышты үшбұрыш салу»: Аяқталуы

Мектеп:Подхоз ЖББНМ: Бекіту «Бір минут» әдісі бойынша сабақты бекіту. Ыстық орындыққа отырған оқушы бір минутта өтілген тақырыпқа байланысты өзінің ақпаратын ұсынады.

Сабақ:«Тікбұрышты үшбұрыш салу»:

Мектеп:Подхоз ЖББНМ:

Бағалау

Үйге тапсырма: №119, 125

Кері байланыс (Рефлексия)

Сабақтан алған әсерім (Сообщение)

Сабақ туралы пікір жазу мен қаншалықты меңгердім?

Сабақ:«Тікбұрышты үшбұрыш салу»: Саралау-Сіз қосымша көмек көрсетуді қалай жоспарлайсыз? Сіз қабілеті жоғары оқушыларға тапсырманы күрделендіруді қалай жоспарлайсыз?

Мектеп:Подхоз ЖББНМ: Бағалау-оқушылардың үйренгенін тексеруді қалай жоспарлайсыз?

Пәнаралық байланыс қауіпсіздік және еңбекті қорғау ережелері

АКТ-мен байланыс

Құндылықтардағы байланыс

Сабақ:«Тікбұрышты үшбұрыш салу»: Дарынды және талантты оқушыларға деңгей бойынша есеп шығару, төмен деңгейдегі оқушыларға оқулықты пайдаланып кесте толтыру жұмысы берілді.

Мектеп:Подхоз ЖББНМ: Қалыптастырушы бағалау әдістері, критерий арқылы бағаланды

Оқушылардың жеке, топтық жұмыс жасау арқылы ұжымдық қарым-қатынас мәдениеті нығая түсті.

Power Point программасында таныстырылым ұсынуда санитарлық ережелер ескерілді.

АКТ пайдалана отырып жұмыстанды. Мәліметтер іздеді.

Математика информатика, пәндерімен байланыс болды.