Алғашқы функция және анықталмаған интеграл: анықтамалар, негізгі қасиеттер және есептер

Сабақтың тақырыбы: Алғашқы функция және анықталмаған интеграл

Сабақтың мақсаты:

Білімділік міндеті:Оқушыларға алғашқы функция мен анықталмаған интегралдың анықтамасы, алғашқы функцияның негізгі қасиетімен танысып, алғашқы функцияны табу ережелерін білу.
Дамытушылық міндеті:Алғашқы функция мен анықталмаған интегралды табу бойынша білім, білік дағдыларын қалыптастыру, алғашқы функцияны табу ережелерін қолдана білу дағдыларын қалыптастырып дамыту.
Тәрбиелік міндеті:

Оқуға саналы сезімге жауапкершілікке, өз бетінше еңбектенуге тәрбиелеу.

Сабақтың көрнекілігі:

Интерактивті тақта
Интерактивті тақтада:

Өткенге шолу: Туынды тарауын қайталау сұрақтары. Туынды кестесі.
Жаңа тақырып бөлімдері, алғашқы функция кестесі
Тест тапсырмасы
Сәйкестік тест

Сабақтың түрі: Жаңа білім беру сабағы

Әдістері: сұрақ - жауап, баяндау, деңгейлік тапсырма, тест тапсырмалары.

Сабақтың барысы:

І. Ұйымдастыру

ІІ. Өткен сабаққа шолу

ІІІ. Жаңа сабақ түсіндіру

ІV. Жаңа білімді меңгерту

Деңгейлік тапсырмалар
Тест тапсырмалар

V. Сабақты қорытындылау

Сәйкестік тест орындау

VI. Бағалау

VII. Үйге тапсырма

І. Ұйымдастыру кезеңі

ІІ. Өткен сабаққа шолу

Туынды анықтамасын айтыңыз, белгілерін формуламен жазыңыз.
Туынды табу кестесін толтыр:

функция

х ⁿ

\sqrt{x}

\sin x

\cos x

tgx

{ctg}x

функция: туындысы

с:

х:

хn:

x\sqrt{x}:

sin⁡x\sin x:

cos⁡x\cos x:

tgxtgx:

ctgx{ctg}x:

ІІІ. Жаңа сабақты түсіндіру:

Туынды табу кестесін пайдаланып: «Туындысы белгілі болған жағдайдабастапқы функцияны» қалай табуға болады?
Алғашқы функция анықтамасы, белгілеуі, мысалдар.
Алғашқы функцияның негізгі қасиеті

F ¹ (x) = f(x)

(F(x) + c) ¹ = f(x)

Алғашқы функцияның геометриялық мағынасы

Ескерту:

Тұрақты шаманы табу ол

алғашқы функцияның біреуін

таңдау

Алғашқы функцияны табу кестесі

Функция

Алғашқы функцияның жалпы түрі

Функция:

f(x) =R

R - тұрақты

Алғашқы функцияның жалпы түрі: F(x) = kx + c

Функция:

f(x) = x ^ɑ

ɑ $\in$ $\in$ Z, ɑ $\neq$ $\neq$ -1

Алғашқы функцияның жалпы түрі:

Функция: f(x) =

\frac{1}{\sqrt{x}}

\frac{1}{\sqrt{x}}

Алғашқы функцияның жалпы түрі: F(x) = 2

\sqrt{x} + C

\sqrt{x} + C

Функция: f(x) = sin x

Алғашқы функцияның жалпы түрі: F(x) = -cos x+C

Функция: f(x) = cos x

Алғашқы функцияның жалпы түрі: F(x) = sin x+C

Функция:

Алғашқы функцияның жалпы түрі: F(x) = tg x +C

Функция:

Алғашқы функцияның жалпы түрі: F(x) =-ctg x +C

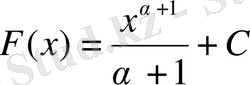
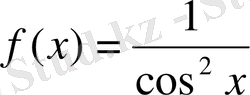
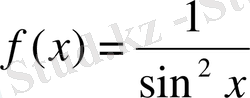
Анықталмаған интеграл анықтамасы, белгілеуі, теңдігі
Алғашқы функцияны табудың үш ережесі, дәлелдеу, мысал

ІV. Жаңа білімді меңгерту. Деңгейлік тапсырмаларА

Есеп

номері

тапсырма

жауабы

Есепномері:

тапсырма:

жауабы: Функция f(х)

Алғашқы функцияны табыңдар F(x) = ?

Есепномері: №1

тапсырма: 2

жауабы: f(x) =4x ² +x-2

F(x) =

\frac{{4x}^{3}}{3} + \ \frac{x^{2}}{2} - \ 2x + c

\frac{{4x}^{3}}{3} + \ \frac{x^{2}}{2} - \ 2x + c

Есепномері:

тапсырма: 4

жауабы: f(x) =

\frac{1}{x^{2}}

\frac{1}{x^{2}}

F(x) = -

\frac{1}{x}

\frac{1}{x}

+ c

Есепномері: №2

тапсырма: 3

жауабы: f(x) =3Cosx - 4Sinx

F(x) = 3Sinx + 4Cosx + c

Есепномері: №3

тапсырма: 2

жауабы: f(x) =x ³ -

\frac{4}{\sqrt{x}}

\frac{4}{\sqrt{x}}

F(x) =

\frac{x^{4}}{4} - \ 8\sqrt{x}

\frac{x^{4}}{4} - \ 8\sqrt{x}

+ c

Есепномері:

тапсырма: 4

жауабы: f(x) = Cos(2x +

\frac{\pi}{6}

\frac{\pi}{6}

)

F(x) =

\frac{1}{2}\ Sin\left( 2x + \ \frac{\pi}{6} \right) + \ c

\frac{1}{2}\ Sin\left( 2x + \ \frac{\pi}{6} \right) + \ c

В №9. 2

Есеп

тапсырма

жауабы:

Есеп: номері

тапсырма:

F(x) функция

M (a; 6) нүкте

жауабы:: Алғашқы функцияның жалпы түрі

Графигі М(а; 6) нүктесі арқылы өтетін F(x) алғашқы функция

Есеп: №9. 2

тапсырма:

f(x) =3x ² - 2

M(2; 4)

жауабы:: F(x) = x ³ - 2x + c

F(2) =2 ³ -2*2+c = 4

4 + c = 4

F(x) = x ³ - 2x

Есеп: №9. 4

тапсырма:

F(x) =3Cosx - 2

M( $\frac{\pi}{2};$ $\frac{\pi}{2};$ -1)

жауабы:: F(x) = 3Sinx - 2x + c

3Sin $\frac{\pi}{2} - 2*\frac{\pi}{2} + c = -$ $\frac{\pi}{2} - 2*\frac{\pi}{2} + c = -$

3- $\pi + c = - 1$ $\pi + c = - 1$ c= $\pi - 4$ $\pi - 4$

F(x) = 3Sinx - 2x + $\pi - 4$ $\pi - 4$

С №14

F1(x) =4x3- 3x2және F(1) =3

f(x) =4x ³ - 3x ² 1 ⁴ - 1 ³ + c = 3, c = 3

F(x) = x ⁴ - x ^{3 + c} F(x) = x ⁴ - x ³ + 3

Тест тапсырмасын орындау

Ұқсас жұмыстар

Алғашқы функция және интеграл: анықтамалар, қасиеттер және практикалық есептер

Алғашқы функция және интеграл: есептер арқылы білімді жүйелеу

Алғашқы функция және интеграл - 11-сынып алгебра сабақ жоспары

Алғашқы функция және интеграл тақырыбы бойынша саралап оқытуды қолданудың әдістемелік сабақ жоспары

Алғашқы функция және интеграл: 11-сыныпқа арналған ҰБТ-ға дайындық сабақ жоспары

Алғашқы функция және интеграл: қисық сызықпен шектелген фигуралардың ауданын есептеуге арналған практикалық сабақ жоспары

8-сыныпқа арналған сабақ: Тіктөртбұрыш, ромб және квадрат - анықтамалар, қасиеттер және есептер

Функция шектері: теория, тамаша шектер және есептер

Механикалық жұмыс және қуат: анықтамалар, формулалар және есептер

Туынды, алғашқы функция және интегралдың қолданылуы: жинақтау сабағының ашық сабақ жоспары

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz