Интегралды есептеуге есептер шығару жайлы

Мұғалімнің аты-
жөні:
Әбдірзақ Мейрім Мақуұлы
Ақтөбе облысы Ойыл ауданы
Амангелді орта мектебінің
математика пәнінің мұғалімі

Сүйікті ісі: Табиғат
аясында серуендеу.
Көл
жағасында қармақпен
балық
аулау.

Педагогикалық ұстанымы:
Математикалық біліммен жан-
жақты
қаруланған, алған білімімен
тәуелсіз еліміздің
өсіп, өркендеуіне үлес қосатын
шәкірт дайындау.

Мектепте математика пәнінің мұғалімі болу неліктен ұнайды ?

Себебі, математика пәні басқа пәндерге қарағанда өзінің қиындығы
мен қызық мол пән. Математика пәнінің осы жақтары мені өзіне
қызықтырады. Математика пәнінен сабақ беру кезінде шығарылу қиындық
келтіретін тапсырмалар не болмаса жауаптары дәл шығпайтын есептер
тобы кездеседі. Осындай тапсырмалардың шешімдерін оқушылармен бірлесе
отырып табу, талдау мұғалімді де, оқушыны да шығармашылықпен жұмыс
істеуге жетелейді. Математика пәнін оқушыларға оқытып, меңгерту арқылы
олардың бойында өмірге деген дұрыс ұтымды көзқарас, жақсы
әлеуметтік жағдай қалыптастыруға, әртүрлі қаржылық талдаулар жасай
білуге және де математикадан алған білімдері арқылы тәуелсіз
еліміздің экономикасын көтеріп, өркендетуге болады. Математика
пәнінің мұғалімі болып жұмыс істеу арқылы осылардың бәріне қол
жеткізуге болады.

11-кластағы математика сабағы.

Сабақ тақырыбы: Интегралды есептеуге есептер шығару.

Сабақ мақсаты: 1) Қисық сызықпен шектелген фигураның ауданын

табуда интегралмен есептеудің
тиімділігін пайдалана

отырып оқушыларға тақырыптық
берілген есептерді

дұрыс, тиімді шығара білу тәсілдерін
меңгерту.

2) Интегралдарды есептеу кестесін
оқушылардың есте

сақтау мүмкіндігін арттыру және
кестедегі формуланы

есептер шығаруда қолдана білуге
дағдыландыру.

3) Оқушылардың тақырыптық есептерді өз
беттерінше

шығара білуге дағдыландыру.

Қолданылған құрал-жабдықтар: Интерактивті тақта, электронды оқулық,

презентация.

Сабақ барысы: І. Ұйымдастыру кезеңі.

ІІ. «Есіңде ме, формула ?» ойыны. (Өтілген формулаларды еске түсіру)

ІІІ. Есептер шығару.

Интегралға берілген есептерді дұрыс шығара білу үшін интегралдар
кестесін жатқа білу керек. Себебі, кез-келген интегралды есептеу,
тапсырма жеңіл болсын немесе күрделі болсын осы кестеге әкеліп
тірейді. Интегралға берілген есептерді әр түрлі жолдармен есептеуге
болады. Бірақ мұғалім оқушыға дұрыс шешімді дәл табуға болатын
тиімді тәсілді меңгертіп үйрету керек.

Шығарылатын есептер үш деңгейде берілгені жөн. Әр деңгейді мына
түрде бөліп көрсетуге болады.

І деңгей: 4 есеп.
ІІ деңгей: 4 есеп.
ІІІ деңгей: 4 есеп.
Әр деңгейдегі есеп санынын мұғалім класс оқушыларының білім
деңгейлеріне қарап өзгертуіне болады.
Әр деңгейдегі тапсырмалардың жартысы үйге берілуі керек. Мәселен,
І деңгейдегі 4 есептің 2-і, ІІ деңгейдегі 4 есептің 2-і, ІІІ
деңгейдегі 4 есептің 2-і. Себебі, оқушы әр деңгейдің
мектепте қарастырылған бөлігін өздігінен шығарсын немесе мұғалім
көмегімен шығарсын әйтеуір мектепте класта шығарады. Ал әр
деңгейдегі үйге берілген қалған бөлігін класта шығарылған есепті
үлгі ретінде пайдаланып өздігінен шығарады.
Деңгейлік тапсырмалардың бәрі «Талапкер» электронды тест жинағынан
алынған.
І деңгей тапсырмасы:
Есеп №23/1951.
Мына сызықтармен шектелген фигураның аудынын табыңыз:
, , .
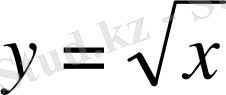Шығарылуы:

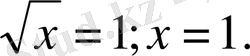
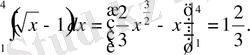Жауабы:
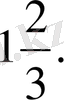
Есеп № 23/1952.
а-ның қандай мәнінде мына сызықтармен шектелген фигураның ауданы 4-
ке тең: у=2х+2, у=0, х=а.
Шығарылуы:
2х+2=0; х= -1.

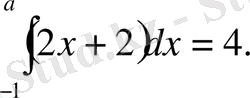
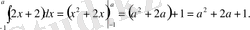
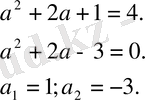Жауабы: 1.
ІІ деңгей тапсырмалары:
Есеп №13/1967.
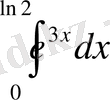интегралын есепте.
Шығарылуы:
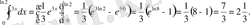
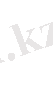Жауаыбы:

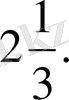
Есеп №2/3.
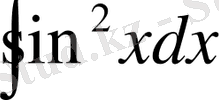интегралын есепте.
Шығарылуы:

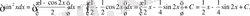
Жауабы:
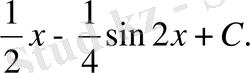
ІІІ деңгей тапсырмалары:
Есеп №3/1.
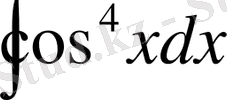интегралын есепте.

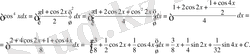
Жауабы:

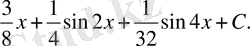
Есеп №3/3.
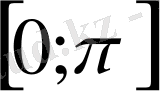аралығында косинусойдасымен ОХ осінің арасындағы фигураның
ауданын табыңыз.
Шығарылуы:
у

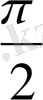0
х

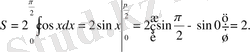
Интеграл таңбасының алдындағы 2 коэфициенті сызбада симметриялы
орналасуына байланысты.
Жауабы: 2.
IV. Үйге тапсырма:
Есеп №23/1953.
Есептеңіз: .
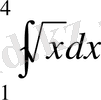Есеп №23/1956.
а-ның қандай мәніндерінде 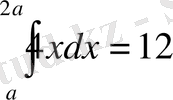теңдеуі дұрыс.
Есеп №12/1968.
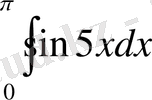интегралын есепте.
Шығарылуы:

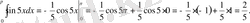
Жауабы:
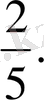
Есеп №2/4.
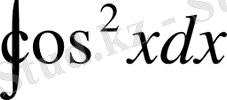интегралын есепте.
Шығарылуы:

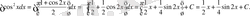
Жауабы:

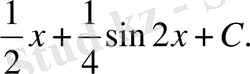
Есеп №3/2
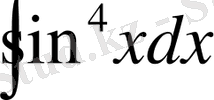интегралын есепте.

Жауабы:
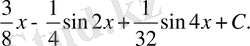
Есеп №3/4.
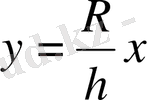түзуі 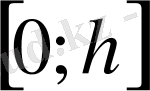кесіндісінің төңірегінде шыр айналсын. Сонда пайда
болған дененің көлемін есептеңіз.
у

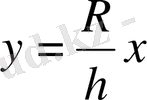
R

0
x

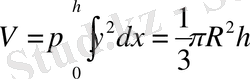
- бұл формула
биіктігі h-қа, табан радиусы
R-ға тең конустың
көлемінің формуласы.

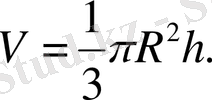
Жауабы:
-----------------------