Сызықтық, квадраттық, рационал-дәрежелі және жоғары дәрежелі теңдеулер: сабақ жоспары мен шешу әдістері


САБАҚ ЖОСПАРЫ
Күні
Тобы
Сабақтың тақырыбы: Сызықтық теңдеу, квадраттық теңдеу және оған келтірілген теңдеу. Рационал-дәрежелі теңдеу
Сабақтың мақсаты:
1. Білімділік: Теңдеуді шешу әдістерін меңгеру.
2. Дамытушылық: Оқушыларды өз бетімен ғылыми ой қорытындыларын жасай білуге жетелеу.
3. Тәрбиелілік: Жауапкершілікке, тиянақтылыққа, еңбекке баулу.
Сабақтың түрі: теориялық
Оқытудың әдістері мен әдістемелік амалдары: баяндау, сұрақ-жауап.
Көрнекті оқу құралдары мен техникалық құралдар: Сызықтық теңдеу, квадраттық теңдеу және оған келтірілген теңдеу. Рационал-дәрежелі теңдеу жалпы түрі мен формулалар жазылған плакаттар.
Сабақтың барысы:
1. Ұйымдастыру бөлімі: Оқушылармен сәлемдесу. Сабаққа даярлығын тексеру.
2. Өткен тақырыпты тексеру: §4 (286-бет) №130-133 [3]
3. Жаңа тақырыпты түсіндіру:
Негізгі формулалар
ах 2 +bx+c=0, a≠0 (1) квадраттық теңдеуінің нақты түбірлері бар болады, егер оның дискриминанты теріс емес болса:
D=b 2 -4ac≥0 (2)
Бұл жағдайда (1) теңдеу түбірлері
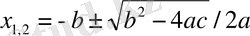 (3) формуласы бойынша табылады.
(3) формуласы бойынша табылады.
Егер
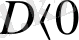 болса, онда (1) теңдеудің нақты тубірдері болмайды.
болса, онда (1) теңдеудің нақты тубірдері болмайды.
ax 2 +bx+c=0 квадрат теңдеуі үшін Виет теоремасы бойынша, теңдеудің
х 1 және х 2 түбірлері және оның коэффициенттері арасындағы келесі қатыстар орындалады:
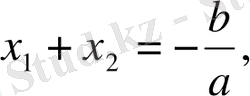
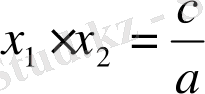 (4)
(4)
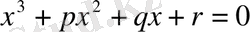 (5) кубтық теңдеу үшін де Виет теоремасы дұрыс:
(5) кубтық теңдеу үшін де Виет теоремасы дұрыс:
 (6)
(6)
1.
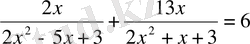
Шешуі:
 мұндағы
мұндағы
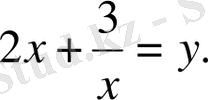
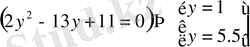
Содан соң х-ты табу үшін келесі теңдеулерді шешеміз:
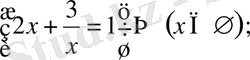
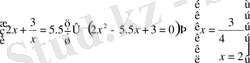 Жауабы:
Жауабы:
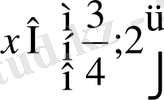
2.
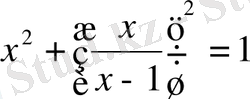
Шешуі:Теңдеудің екі жағына да
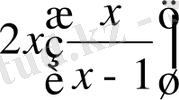 өрнегін қосып, түрлендіру жүргіземіз:
өрнегін қосып, түрлендіру жүргіземіз:
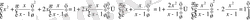
 деп белгілесек, аламыз:
деп белгілесек, аламыз:
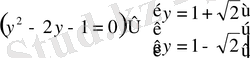
у-тің орнына мәндерін қойып, х-ті табамыз:
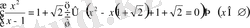 ;
;
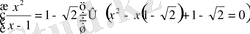
Жауабы:
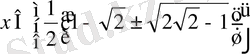
4. Жаңа тақырыпты бекіту:
1)
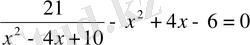 теңдеуін шешу.
теңдеуін шешу.
Шешуі: оған тең күшті
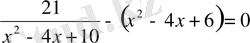 теңдеуін қарастырамыз.
теңдеуін қарастырамыз.
 деп белгілейміз, сонда у-ті табу үшін мына теңдеуді аламыз:
деп белгілейміз, сонда у-ті табу үшін мына теңдеуді аламыз:

У-тің орнына мәндерін қойып, аламыз:
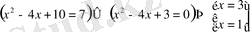
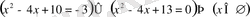
Жауабы:
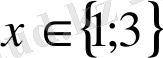 .
.
2)
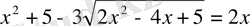
Шешуі:Түрлендіріп аламыз:
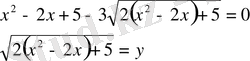
деп белгілейміз, сонда

Берілген теңдеу
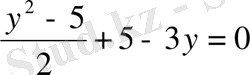 түріне келеді.
түріне келеді.
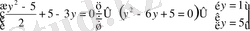
Содан соң келесі екі теңдеуді шешеміз.


Жауабы:
 .
.
5. Үйге тапсырма беру: §4 (286-бет) №136-141 [3]
САБАҚ ЖОСПАРЫ
Күні
Тобы
Сабақтың тақырыбы: Сызықтық теңдеу, квадраттық теңдеу және оған келтірілген теңдеу. Рационал-дәрежелі теңдеу
Сабақтың мақсаты:
1. Білімділік: Теңдеуді шешу әдістерін меңгеру.
2. Дамытушылық: Оқушыларды өз бетімен ғылыми ой қорытындыларын жасай білуге жетелеу.
3. Тәрбиелілік: Жауапкершілікке, тиянақтылыққа, еңбекке баулу.
Сабақтың түрі: теориялық
Оқытудың әдістері мен әдістемелік амалдары: баяндау, сұрақ-жауап.
Көрнекті оқу құралдары мен техникалық құралдар: Сызықтық теңдеу, квадраттық теңдеу және оған келтірілген теңдеу. Рационал-дәрежелі теңдеу жалпы түрі мен формулалар жазылған плакаттар.
Сабақтың барысы:
1. Ұйымдастыру бөлімі: Оқушылармен сәлемдесу. Сабаққа даярлығын тексеру.
2. Өткен тақырыпты тексеру: §4 (286-бет) №130-133 [3]
3. Жаңа тақырыпты түсіндіру:
Негізгі формулалар
ах 2 +bx+c=0, a≠0 (1) квадраттық теңдеуінің нақты түбірлері бар болады, егер оның дискриминанты теріс емес болса:
D=b 2 -4ac≥0 (2)
Бұл жағдайда (1) теңдеу түбірлері
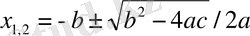 (3) формуласы бойынша табылады.
(3) формуласы бойынша табылады.
Егер
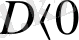 болса, онда (1) теңдеудің нақты тубірдері болмайды.
болса, онда (1) теңдеудің нақты тубірдері болмайды.
ax 2 +bx+c=0 квадрат теңдеуі үшін Виет теоремасы бойынша, теңдеудің
х 1 және х 2 түбірлері және оның коэффициенттері арасындағы келесі қатыстар орындалады:
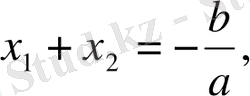
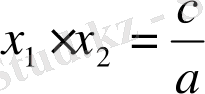 (4)
(4)
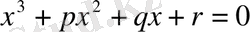 (5) кубтық теңдеу үшін де Виет теоремасы дұрыс:
(5) кубтық теңдеу үшін де Виет теоремасы дұрыс:
 (6)
(6)
1.
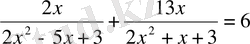
Шешуі:
 мұндағы
мұндағы
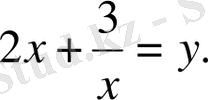
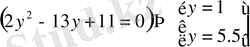
Содан соң х-ты табу үшін келесі теңдеулерді шешеміз:
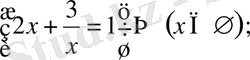
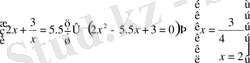 Жауабы:
Жауабы:
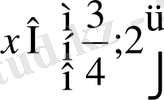
2.
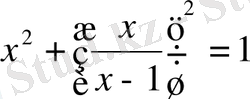
Шешуі:Теңдеудің екі жағына да
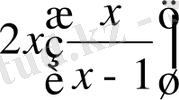 өрнегін қосып, түрлендіру жүргіземіз:
өрнегін қосып, түрлендіру жүргіземіз:
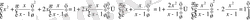
 деп белгілесек, аламыз:
деп белгілесек, аламыз:
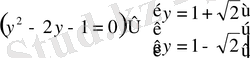
у-тің орнына мәндерін қойып, х-ті табамыз:
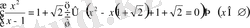 ;
;
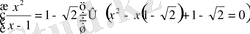
Жауабы:
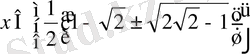
4. Жаңа тақырыпты бекіту:
1)
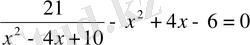 теңдеуін шешу.
теңдеуін шешу.
Шешуі: оған тең күшті
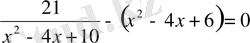 теңдеуін қарастырамыз.
теңдеуін қарастырамыз.
 деп белгілейміз, сонда у-ті табу үшін мына теңдеуді аламыз:
деп белгілейміз, сонда у-ті табу үшін мына теңдеуді аламыз:

У-тің орнына мәндерін қойып, аламыз:
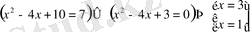
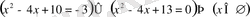
Жауабы:
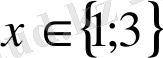 .
.
2)
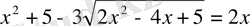
Шешуі:Түрлендіріп аламыз:
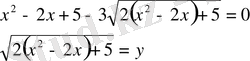
деп белгілейміз, сонда

Берілген теңдеу
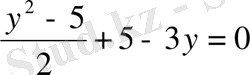 түріне келеді.
түріне келеді.
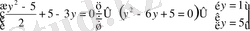
Содан соң келесі екі теңдеуді шешеміз.


Жауабы:
 .
.
5. Үйге тапсырма беру: §4 (286-бет) №136-141 [3]
Алгебралық теңдеулер
4. Мысал:
 если
если
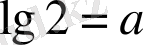
Шешуі

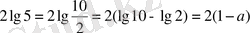
Мысал:
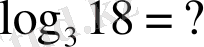 если
если

1 әдіс.
 .
.
Енді
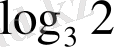 табамыз, ол үшін
табамыз, ол үшін
 санын
санын
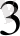 және
және
 бойынша өрнектейміз.
бойынша өрнектейміз.
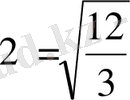 . Онда
. Онда
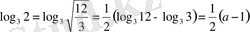 .
.
сонымен
 .
.
2 әдіс.
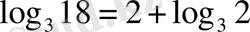 .
.
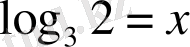 деп белгілейміз, онда
деп белгілейміз, онда
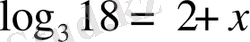 . Ендеше,
. Ендеше,
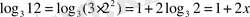
Шарт бойынша
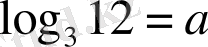 , олай болса
, олай болса
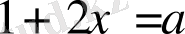 , бұдан
, бұдан
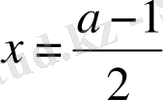
сонымен
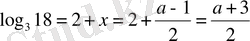 .
.
Мысал
:
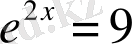 , онда
, онда
 . негізі бойынша логарифмдейміз
. негізі бойынша логарифмдейміз
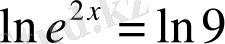 ,
,
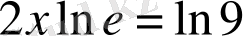 ,
,
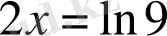 бұдан
бұдан
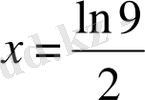
Мысал:
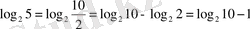 .
.
Теңсіздікті дәлелдеу
1.
a+b+c >=
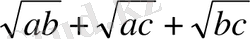

(
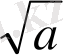 -
-
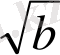 )
2
>=0 a+b>=2
)
2
>=0 a+b>=2

(
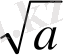 -
-
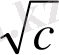 )
2
>=0 a+c>=2
)
2
>=0 a+c>=2
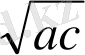
(
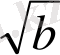 -
-
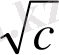 )
2
>=0 b+c>=2
)
2
>=0 b+c>=2
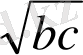
2(a+b+c) >= 2(
 +
+
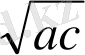 +
+
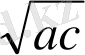 )
)
a+b+c>=
 +
+
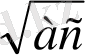 +
+
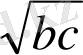
2. (a+b) (b+c) (a+c) =8a*b*c
(
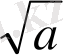 -
-
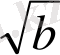 )
2
>=0 a+b>=2
)
2
>=0 a+b>=2

(
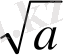 -
-
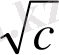 )
2
>=0 a+c>=2
)
2
>=0 a+c>=2
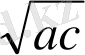
(
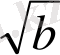 -
-
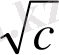 )
2
>=0 b+c>=2
)
2
>=0 b+c>=2
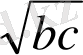
. (a+b) (b+c) (a+c) =8a*b*c
3. a>=0 b>=0 c>=0 a+b+c=1
(
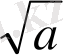 -
-
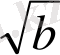 )
2
>=0 a+b>=2
)
2
>=0 a+b>=2

(
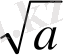 -
-
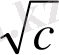 )
2
>=0 a+c>=2
)
2
>=0 a+c>=2
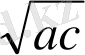
(
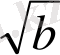 -
-
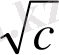 )
2
>=0 b+c>=2
)
2
>=0 b+c>=2
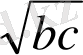
(a+b) (b+c) (a+c) =8a*b*c a=1-b-c
b=1-a-c
c=1-a-b
(1-b-c+b) (1-a-c+c) (1-b-a+a) >8a*b*c
(1-c) (1-a) (1-b) >8a*b*c
4. a>=0 b>=0 c>=0
(a+1) (b+1) (c+a) (b+c) >=16a*b*c
(
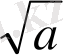 +1)
2
>=0 a+1>=2
+1)
2
>=0 a+1>=2
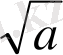
(
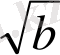 +1)
2
>=0 b+1>=2
+1)
2
>=0 b+1>=2
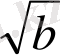
(
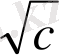 +
+
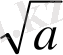 )
2
>=0 c+a>=2
)
2
>=0 c+a>=2
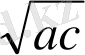
(
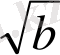 -
-
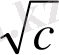 )
2
>=0 b+c>=2
)
2
>=0 b+c>=2
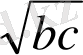
(a+1) (b+1) (c+a) (b+c) >=16a*b*c
5.
log 2 3+log 3 2>2
log 3 3/log 2 3+log 3 2>2
(1+log 3 2 2) /log 2 3>2
1+log 3 2 2>2log 3 2
(1+log 3 2) 2 >0

6. (a
2
+2 ) /
 >=2
>=2
. (a
2
+2 ) /
 -2=a
2
+2-2
-2=a
2
+2-2
 =(
=(
 -1)
2
/
-1)
2
/

7
a>=0 b>=0 c>=0 d>=0
a 4 +b 4 +c 4 +d 4 >4a*b*c*d
(a 2 -b 2 ) 2 +2a 2 b 2 +(c 2 -d 2 ) +2c 2 d 2 >=4a*b*c*d
(a 2 -b 2 ) 2 +2a 2 b 2 +(c 2 -d 2 ) +2c 2 d 2 - 4a*b*c*d>=0
(a 2 -b 2 ) 2 +(c 2 -d 2 ) +2(a 2 b 2 -2abcd+c 2 d 2 ) >=0
(a 2 -b 2 ) 2 +(c 2 -d 2 ) 2 +2(ab-cd) 2 >=0
- a>=0 b>=0 c>=0 d>=0
=<
(a+c) +
(b+d)

(
+
) 2 >=0
a+b-2
+c+d>=0
(a+b+c+d) >=

=<
(a+c) +
(b+d)
9. a 1 >=0 a 2 >=0 … a n >=0
+
+…. +
+
+…. +
+…+
=>
(a 1 +a 2 +…. +a n )
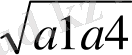
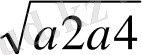
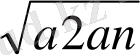

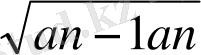
n=4
+
+
+
+
+
=<
(a 1 +a 2 +a 3 +a 4 )
a 1 +a 2 =<2
a 2 +a 3 =<2
a 3 +a 4 =<2

a 1 +a 3 =<2
a 2 +a 4 =<2
………
a 1 +a 4 =<2
………. . a 3 +a n =<2
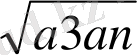
………. . . a 2 +a n =<2
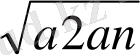
a 1 +a n =<2
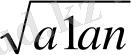

Жоғары дәрежелі теңдеулер
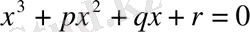 (7) кубтық теңдеуін қарастырайық.
(7) кубтық теңдеуін қарастырайық.
Егер p, q, r коэффициенттері- бүтін сандар болса, онда (7) теңдеудің бүтін түбірлерін r бос мүшесінің бөлгіштерінің ішінен іздеу қажет. Бұл (6) қатыстан шығады. Егер х 1 бүтін түбірін тапсақ,
 көпмүшесін (х-х
1
) -ге бөлеміз. Бөлінді де -екінші дәрежелі көпмүше. Оны 0-ге теңестіріп, квадрат теңдеу аламыз.
көпмүшесін (х-х
1
) -ге бөлеміз. Бөлінді де -екінші дәрежелі көпмүше. Оны 0-ге теңестіріп, квадрат теңдеу аламыз.
1.
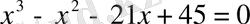 теңдеуін шешу.
теңдеуін шешу.
Шешуі. Бүтін түбірлерді бос мүшенің бөлгіштері:
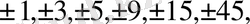 сандарының ішінен іздейміз. Бұл сандарды тексере отырып,
сандарының ішінен іздейміз. Бұл сандарды тексере отырып,
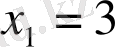 түбірін табамыз.
түбірін табамыз.
 көпмүшесін (х-3) -ке бөлеміз, бөліндіде
көпмүшесін (х-3) -ке бөлеміз, бөліндіде
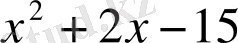 көпмүшесін аламыз. Сонан соң
көпмүшесін аламыз. Сонан соң
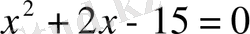
Теңдеуін шешеміз. Оның екі түбірі бар: x=3, x=5.
Жауабы:
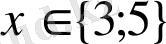 .
.
2.
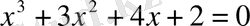 теңдеуін шешеміз.
теңдеуін шешеміз.
Шешуі: Бүтін түбірлерін
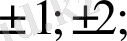 сандарының ішінен іздейміз. Тексере отырып,
сандарының ішінен іздейміз. Тексере отырып,
 аламыз.
аламыз.
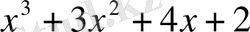 - ні
- ні
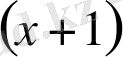 -ге бөлеміз және
-ге бөлеміз және
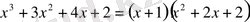 .
.
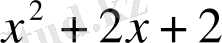 -ні 0-ге теңестіріп,
-ні 0-ге теңестіріп,
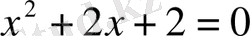 квадрат теңдеуін шешеміз.
квадрат теңдеуін шешеміз.
 болғандықтан, бұл теңдеудің нақты түбірлері болмайды.
болғандықтан, бұл теңдеудің нақты түбірлері болмайды.
Жауабы:
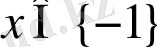
3.
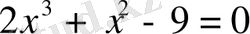 теңдеуін шешу.
теңдеуін шешу.
Шешуі:Бос мүшенің бөлгіштері:
 Бүтін түбірлері болмайтынына көз жеткіземіз. Бұл теңдеудің мүмкін болатын рационал түбірлерін іздеу үшін теңдеудің екі жағын 4-ке көбейтеміз:
Бүтін түбірлері болмайтынына көз жеткіземіз. Бұл теңдеудің мүмкін болатын рационал түбірлерін іздеу үшін теңдеудің екі жағын 4-ке көбейтеміз:
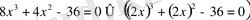 .
.
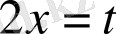 алмастыруы түбірі
алмастыруы түбірі

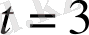 болатын
болатын
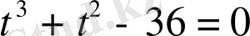

 теңдеуіне әкеледі. Әрі қарай
теңдеуіне әкеледі. Әрі қарай
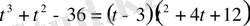 ;
;
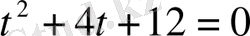 теңдеуінің нақты түбірлері болмайды, сондықтан
теңдеуінің нақты түбірлері болмайды, сондықтан
 түбірі, демек
түбірі, демек
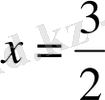 -берілген теңдеудің жалғыз түбірі болып табылады.
-берілген теңдеудің жалғыз түбірі болып табылады.
Төртінші дәрежелі және жоғары дәрежелі теңдеулер осыған ұқсас шешіледі.
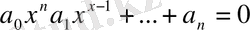 (8) мұндағы
(8) мұндағы
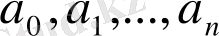 бүтін сандар, теңдеуінің рационал түбірлерін іздеу үшін әр түрлі әдістер қолданылады.
бүтін сандар, теңдеуінің рационал түбірлерін іздеу үшін әр түрлі әдістер қолданылады.
Олардың бірі (8) теңдеуінің рационал түбірлерін
 , мұндағы
, мұндағы
 -ң бөлгіші,
-ң бөлгіші,
 -ң бөлгіші және
-ң бөлгіші және
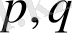 - өзара жай, түрінде іздеуден тұрады. Осы әдістерді мысал арқылы сипаттайық.
- өзара жай, түрінде іздеуден тұрады. Осы әдістерді мысал арқылы сипаттайық.
4.
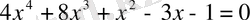 теңдеуін шешу.
теңдеуін шешу.
Шешуі: теңдеудің екі жағын 4-ке көбейтеміз және
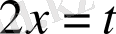 алмастыруын жүргізіп, мынаны аламыз.
алмастыруын жүргізіп, мынаны аламыз.
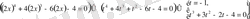
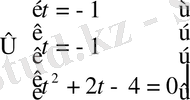
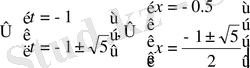
Жауабы:
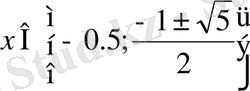
Осы теңдеудің басқа тәсілмен шешсек, оны мына түрге келтіреміз:
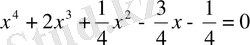 бос мүшенің бөлгіштері:
бос мүшенің бөлгіштері:
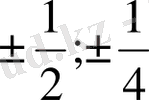 . Бұл сандарды тексере отырып,
. Бұл сандарды тексере отырып,
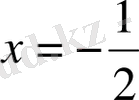 табамыз.
табамыз.
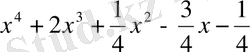 көпмүшесін
көпмүшесін
 -ге бөлуді орындап, бөлінді де
-ге бөлуді орындап, бөлінді де
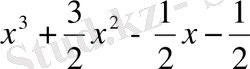 көпмүшесін аламыз. Бұл көпмүшенің
көпмүшесін аламыз. Бұл көпмүшенің
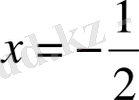 түбірін аналогиялы түрде табамыз. Әрі қарай
түбірін аналогиялы түрде табамыз. Әрі қарай
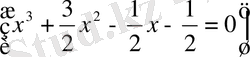
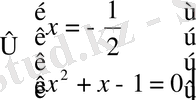
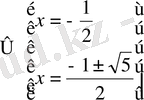
жауабы :
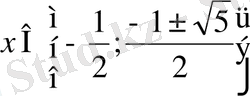
Теңдеуді шешіңіз:
Алмастыру тәсілі
Көптеген алгебралық теңдеулер алмастыру арқылы квадрат теңдеулерге не жоғары дәрежелі теңдеулерге келеді. Бірнеше мысал келтірейік.
Егер
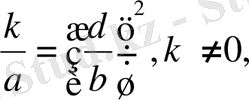 шарты орындалса, онда ax
4
+bx
3
+cx
2
+dx+k=0 түріндегі теңдеу қайтарымды деп аталады. X=0-қайтарымды теңдеудің шешімі бола алмайтындықтан, теңдеудің екі жағын да х
2
-қа бөліп және айнымалылардың сәйкес алмастыруынан соң квадрат теңдеу алуға болады. Қайтарымды теңдеуді шешуге мысал келтірейік.
шарты орындалса, онда ax
4
+bx
3
+cx
2
+dx+k=0 түріндегі теңдеу қайтарымды деп аталады. X=0-қайтарымды теңдеудің шешімі бола алмайтындықтан, теңдеудің екі жағын да х
2
-қа бөліп және айнымалылардың сәйкес алмастыруынан соң квадрат теңдеу алуға болады. Қайтарымды теңдеуді шешуге мысал келтірейік.
- 2х4-21х3+74х2-105х+50=0
Шешуі: Теңдеулің екі жағын х 2 -қа бөліп, қосылғыштарды топтаймыз:
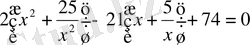
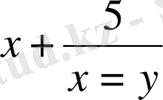 белгілеуін енгіземіз, сонда
белгілеуін енгіземіз, сонда
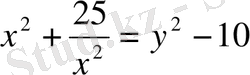 аламыз.
аламыз.

Сонымен,
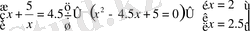

Жауабы:
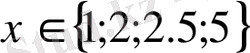 .
.
Қайтарымды теңдеудің жеке жағдайлары болып симметриялы деп аталатын ах
4
+bx
3
+cx
2
+bx+a=0 түріндегі теңдеу (ұштарынан бірдей қашықтықтағы мүшелер коэффициенттері бірдей) және қиғаш симметриялы деп аталатын ах
4
+bx
3
+cx
2
-bx+a=0 түріндегі теңдеу (ұштарынан бірдей қашықтықта жұп дәрежелі мүшелер коэффициенттері тең, ал тақ дәрежелі мүшелер коэффициенттері абсолют шамасы жағынан тең және таңбалары қарама-қарсы) табылады. Симметриялы теңдеу
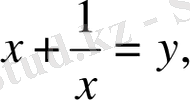 қиғаш симметриялы теңдеу
қиғаш симметриялы теңдеу
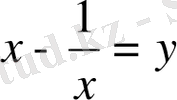 алмастыруы арқылы квадрат теңдеулерге келеді.
алмастыруы арқылы квадрат теңдеулерге келеді.
Егер а+b=c+d шарты орындалса, (х+а) (x+b) (x+c) (x+d) =m түріндегі теңдеу квадрат теңдеуге келтіріледі.
- (x-1) x(x+1) (x+2) =24 теңдеуін шешу.
Шешуі: түрлендіру жүргізіп, аламыз:(x 2 +x) (x 2 +x-2) =24 x 2 +x=y белгілеуін енгіземіз, сонда

Х-ті табу үшін екі теңдеу жиынтығын шешеміз:
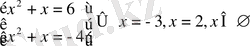
Жауабы:
.
Теңдеуді шешеңіз:
25. (x+3) 4 +(x+5) 4 =16 теңдеуін шешу.
Шешуі: x+4=t алмастыруын жасаймыз. Сонда
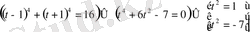
(x+4) 2 =1 теңдеуін шешіп, x=-3, x=-5 табамыз.
t 2 =-7теңдеуінің нақты түбірлері болмайды.
Жауабы:
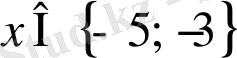 .
.
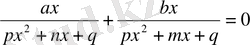 түріндегі теңдеу әрбір бөлшектің алымын да, бөлімін де х-ке бөлу арқылы
түріндегі теңдеу әрбір бөлшектің алымын да, бөлімін де х-ке бөлу арқылы
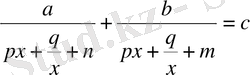 түріне келеді.
түріне келеді.
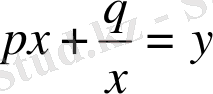 деп белгілеп, квадрат теңдеуге апаратын
деп белгілеп, квадрат теңдеуге апаратын
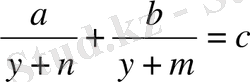 теңдеуін аламыз.
теңдеуін аламыз.
26.
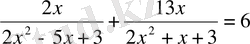
Шешуі:
 мұндағы
мұндағы
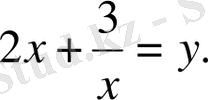
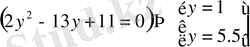
Содан соң х-ты табу үшін келесі теңдеулерді шешеміз:
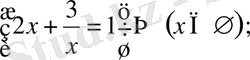
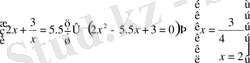 Жауабы:
Жауабы:
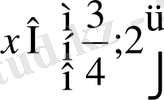
27.
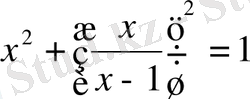
Шешуі:Теңдеудің екі жағына да
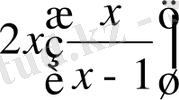 өрнегін қосып, түрлендіру жүргіземіз:
өрнегін қосып, түрлендіру жүргіземіз:
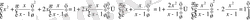
 деп белгілесек, аламыз:
деп белгілесек, аламыз:
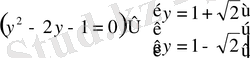
у-тің орнына мәндерін қойып, х-ті табамыз:
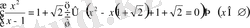 ;
;
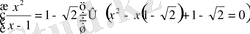
Жауабы:
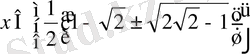
28. (6х+7) 2 (3x+4) (x+1) =6 теңдеуін шешу.
Шешуі: Қарапайым түрлендіру жүргізіп аламыз:
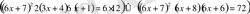
6x+7=t алмастыруын жасап аламыз:
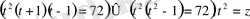 деп белгілейік, Сонда:
деп белгілейік, Сонда:
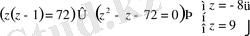 z-тің орнына мәндерді қойып аламыз:
z-тің орнына мәндерді қойып аламыз:
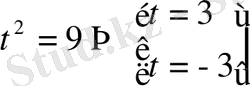
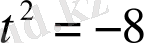 теңдеуінің нақты түбірі болмайды.
теңдеуінің нақты түбірі болмайды.
t=6x+7 екенін ескеріп, х-ті табу үшін мына теңдеулерді шешеміз:
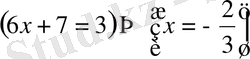
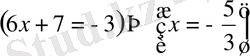
Жауабы:
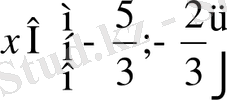 .
.
Теңдеулерді шешіңіз:
ау
2а
+ву
а
z
a
+cz
2a
=0 (9) түріндегі теңдеу бірыңғай теңдеу деп аталады, мұндағы а, в, с,
 -нөлден өзге берілген сандар у және z x-тн алынған қайсыбір функциялар.
-нөлден өзге берілген сандар у және z x-тн алынған қайсыбір функциялар.
(9) теңдеуді шешерде z(x) =0 теңдеудің түбірлері (9) теңдеу түбірі бола ала ма, соны тексереміз. Содан соң (9) теңдеудің екі жағын да z 2a -не бөліп аламыз.
 а(y/z)
2a
+b(y/z)
a
+c=0
а(y/z)
2a
+b(y/z)
a
+c=0
(y/z) =t деп белгілеп, t-ға қатысты квадрат теңдеу аламыз.
Бірыңғай теңдеулерді шешуге мысал келтірейік.
45. 3 (x-2) 2 + 3 (x-3) 2 =5/2 3 (x-2) (x-3)
Шешуі: х=3 теңдеудің түбірі болмайтындықтан, теңдеудің екі жағын 3 (x-3) 2 -қа бөлуге болады:
3 ((x-2) /(x-3) ) +1=5/2 3 (x-2) (x-3)
3
(x-2) (x-3) =y деп белгілесек: (y
2
+1=5y/2)
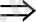 [y=0, 5; y=2 y-тің орнына мәндерін қойып аламыз:
[y=0, 5; y=2 y-тің орнына мәндерін қойып аламыз:
(
3
(x-2) /(x-3) =2)
 ( (x-2) /(x-3) =8)
( (x-2) /(x-3) =8)
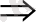 (x=22/7),
(x=22/7),
(
3
(x-2) /(x-3) =1/2)
 ( (x-2) /(x-3) =1/8)
( (x-2) /(x-3) =1/8)
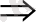 (x=13/7)
(x=13/7)
Жауабы: х
 {13/7; 22/7}
{13/7; 22/7}
46. 3(x 2 -x+1) 2 -2(x+1) 2 =5(x 3 +1) .
Шешуі: x=-1 теңдеудің түбірі болмайтындықтан, теңдеудің екі жағын (x+1) 2 -қа бөлеміз:
(3((x
2
-x+1) /(x+1) )
2
-2=5((x
3
+1) /(x+1)
2
)
 (3((x
2
-x+1) /(x+1) )
2
-2=5(((x
2
-x+1) /(x+1) )
(3((x
2
-x+1) /(x+1) )
2
-2=5(((x
2
-x+1) /(x+1) )
(x
2
-x+1) /(x+1) =t деп белгілейміз, сонда (3t
2
-5t-2=0)
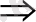 [t=-1/3; t=2] t-нің орнына мәндерін қойып, х-ты табамыз:
[t=-1/3; t=2] t-нің орнына мәндерін қойып, х-ты табамыз:
[ (x
2
-x+1) /(x+1) =2; (x
2
-x+1) /(x+1) =-1/3
 [ x
2
-x+1=2x+2; 3x
2
-2x+4=0
[ x
2
-x+1=2x+2; 3x
2
-2x+4=0
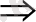 [ x=(3+-13) /2, x
[ x=(3+-13) /2, x

Жауабы: х
 {(3+-
{(3+-
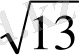 ) /2}
) /2}
Теңдеулерді шешіңіз:
 Тең күшті теңдеулер
Тең күшті теңдеулер
Екі f 1 (x) =g 1 (x) және f 2 (x) =g 2 (x) (1) теңдеулері тең күшті(эквивалентті) деп аталады, егер олардың барлық шешімдерінің жиыны беттесетін болса немесе екуінің де шешімдері болмаса.
Тең күштілік анықтамасынан берілген теңдеудің орнына оған тең күшті теңдеу шешуге болатындығы шығады.
Тең күштілік ұғымы транзитивтілік қасиетке ие, яғни, егер f(x) =g(x) теңдеуі
 (х) =
(х) =
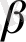 (x) теңдеуіне тең күщті және
(x) теңдеуіне тең күщті және
 (х) =
(х) =
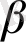 (x) теңдеуі m(x) =p(x) теңдеуіне тең күшті болса, онда f(x) =g(x) теңдеуі m(x) =p(x) теңдеуіне тең күшті болады.
(x) теңдеуі m(x) =p(x) теңдеуіне тең күшті болса, онда f(x) =g(x) теңдеуі m(x) =p(x) теңдеуіне тең күшті болады.
Теңдеуді оған тең күшті теңдеумен немесе теңдеуді оған тең күшті теңдеулер (теңсіздіктер, жүйе) жиынтығымен алмастыру тең күшті көшіру деп аталады.
Мысалы: 1. а) x=1теңдеуі
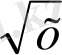 =1теңдеуімен тең күшті, өйткені 1 саны теңдеулердің әрқайсысының түбірі болады және бұл теңдеулердің ешқайсысында да басқа түбірлер жоқ.
=1теңдеуімен тең күшті, өйткені 1 саны теңдеулердің әрқайсысының түбірі болады және бұл теңдеулердің ешқайсысында да басқа түбірлер жоқ.
б) x(x-1) =0 және x(x-1) (x-2) =0 теңдеулері тең күшті болып табылмайды, өйткені 2 саны бір теңдеудің түбірі болғанымен екіншісінің түбірі болмайды.
Теңдеулерді шешкенде теңдеуледің тең күштілігі ұғымының орнына теңдеулердің жиында тең күштілігі ұғымы жиі қолданылады: екі теңдеу А жиынында тең күшті деп аталады, егер олардың А жиынына тиісті болатын барлық түбірлерінің жиыны беттесетін болса немесе олардың екеуінің де осы жиында шешімі болмаса.
Теңдеулер тең күшті болмағанмен де қайсыбір жиында тең күшті болуы мүмкін. Оң сандар жиынында тең күшті болатын x=1 және x=1 теңдеулері мысал бола алады, бірақ олар тең күшті болып табылмайды.
Егер берілген (1) теңдеулер қосы үшін бірінші теңдеудің кез-келген түбірі екінші теңдеудің түбірі болып табылса, онда екінші теңдеу бірінші теңдеудің салдары деп аталады және былай жазылады:
f
1
(x) =g
1
(x)
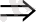 f
2
(x) =g
2
(x)
f
2
(x) =g
2
(x)
Егер теңдеуді оның салдарымен ауыстырса, онда екінші теңдеудің шешімдері жиынында алғашқы теңдеудің барлық түбірлері болады және және олардан басқа алғашқы теңдеудің бөгде түбірлері деп аталатын қайсыбір сандар болуы мүмкін. Сондықтан, егер шешу барысында теңдеуден оның салдарына көшсе, онда шешу соңында түбірлерге зерттеу(тексеру) жүргізу қажет.
Мысалы,
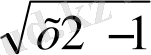 =
=

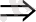 x
2
-1=x
4
-1
x
2
-1=x
4
-1
Екінші теңдеуді шешіп, х 1 =-1, x 2 =0, x 3 =1 табамыз, бірақ 0 саны бірінші теңдеудің түбірі болып табылмайды.
Бұл мысал x 2 =0 бөгде (бірінші теңдеу үшін) түбірі екінші теңдеудің ММО бірінші теңдеудің ММО-нан кңірек болғандығы салдарынан пайда болып отырғандығын көрсетеді. Дегенмен теңдеуден оның салдарына көшкенде теңдеудің ММО-ның кеңеюі әруақытта бола бермейді. (мысал1б-ны қарңыз) .
Теңдеуді шешу процесі әдетте теңдеуді анағұрлым қарапайым теңдеумен біртіндеп алмастырудан немесе оны теңдеулер(теңсіздіктер, жүйелер) жиынтығымен алмастырудан тұрады. Теңдеудің бір немесе екі жағына қандай да бір түрлендіру жүргізіп алғашқы теңдеуді алмастыратын жаңа теңдеу аламыз.
Мысал арқылы теңдеуді түрлендіру оған тең күшті теңдеуге әкелумен қатар, берілгенге тең күшті емес теңдеуге де әкелу мүмкіндігін көрсетейік.
Мысал 2. 7-2х+5/(x-2) -5/(x-2) =11-4x теңдеуі оның сол жағындағы ұқсас мүшелерді біріктіргеннен кейін оған тең күшті 7-2х=11-4х теңдеуімен алмастырылады. 2саны емес 7-2х=11-4х теңдеуінің жалғыз түбірі болғанмен алғашқы теңдеудің түбірі болып табылмайды.
Мысал 3. 5+2х+5/(x-2) -5/(x-2) =26-х теңдеуі ұқсас мүшелерін біріктіргеннен кейін оған тең күшті 5+2х=26-х теңдеуімен алмастырылады. 7саны 5+2х=26-х теңдеуінің де алғашқы теңдеудің де жалғыз түбірі болып табылады.
Мысал 4. (x 2 -1) /(x-1) =2 теңдеуі оның сол жағын х-1 ортақ көбейткішіне қысқартқаннан кейін алғашқыға тең күшті емес х+1=2 теңдеуімен алмасады. 1 саны салдардың жалғыз түбірі болғанмен алғашқы теңдеудің түбірі болып табыллмайды.
Мысал 5. (x 2 -1) /(x-1) =5 теңдеуі оныңсол жағын х-1 ортақ көбейткішіне қысқартқаннан кейін алғашқыға тең күшті х+1=5 теңдеуімен алмасады. 4саны х+1=5 теңдеуінің де алғашқы теңдеудің де түбірі болып табылады.
Теңдеулердің тең күштілігі туралы тұжырымдар.
- f(x) =g(x) және f(x) -g(x) =0 теңдеулері тең күшті.
- f(x) =g(x) және f(x) +=g(x) +теңдеулері кез-келгенсаны үшін тең күшті.
- f(x) =g(x) жәнеf(x) =g(x) теңдеулері кез-келген0 үшін тең күшті.
- аf(x) =ag(x) (a>0, a1) және f(x) =g(x) теңдеулері тең күшті
- Қайсыбір А жиынында y=f(x) және y= g(x) функциялары теріс емес болсын. Онда осы А жиынында f(x) =g(x) және fn(x) =gn(x) (nN) теңдеулеері тең күшті болады.
- y=(x) функциясы анықталған және f(x) =g(x) ММО құрамындағы А жиынының бірде-бір нүктесінде 0-ге ұмтылмайтын болсын. Сонда А жиынында f(x) =g(x) және f(x) (x) =g(x) (x) теңдеулері тең күшті. А жиыны f(x) =g(x) теңдеуінің ММО-мен бнттесуі мүмкін.
Салдарлар туралы тұжырымдар
1. f
2n
(x) =g
2n
(x) (n
 N) теңдеуі f(x) =g(x) теңдеуінің салдары болып табылады.
N) теңдеуі f(x) =g(x) теңдеуінің салдары болып табылады.
2. f(x) =g(x)
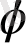 (x) теңдеуі f(x) /g(x) = g(x) теңдеуінің салдары болып табылады.
(x) теңдеуі f(x) /g(x) = g(x) теңдеуінің салдары болып табылады.
3. f(x) =g(x) теңдеуі f(x) +h(x) =g(x) +h(x) теңдеуінің салдары болып табылады.
4. [f(x) =0; g(x) =0 теңдеулер жиынтығы f(x) g(x) =0 теңдеуінің салдары болып табылады.
Мысал 6. х+7+10/(2x-1) =8-x+10/(2x-1) және x+7=8-x теңдеулері тең күшті болып табыла ма?
Шешуі. Екінші теңдеу бірінші теңдеудің екі жағына x=1/2-де анықталмаған 10/(2х-1) өрнегін қосқаннан алынған. Бұл ½ санының бірінші теңдеу түбірі ьола алмағанымен екінші теңдеу түбірі болатындығын білдіреді. ½ санының екінші теңдеу түбірі болатындығын тексеру оңай. Сонымен, екінші теңдеудің ½ түбірі бірінші теңдеудің түбірі бола алмайды. Олай болса, берілген теңдеулер тең күшті болып табылмайды.
Мысал 7. (2(х-10) /(х 2 -13х+30) =1 және x 2 -15x+50=0 теңдеулері тең күшті болып табыла ма?
Шешуі. Бірінші теңдеуді шешеміз. Берілген теңдеудің екі жағын да х 2 -13х+30 өонегіне көбейтіп, бөлімінен құтыламыз, 2х-20= х 2 -13х+30 теңдеуін аламыз. Бұл теңдеудің барлық түбірлерінің жиыны екі саннан тұрады: x 1 =10 және x 2 =5.
Жүргізілген түрлендірудің нәтижесінде бөгде түбірлер пайда болуы мүмкін; сондықтан тексеру қажет. Тексеру x 1 =10 санының берілген теңдеудің түбірі болмайтындығын, ал x 2 =5 саны оның түбірі болатындығын көрсетеді, яғни бірінші теңдеудің жалғыз x=5 түбірі болады.
x 2 -15x+50=0 теңдеуінің x 1 =5 және x 2 =10 екі шешімі бар. Берілген теңдеулердің түбірлері жиынын салыстыра отырып, екінші теңдеудің бірінші теңдеу салдары болатындығын аламыз.
Мысал 8.
 =
=
 және x
2
+x-5=x-1 теңдеулері тең күшті болып табыла ма?
және x
2
+x-5=x-1 теңдеулері тең күшті болып табыла ма?
Шешуі. Екінші теңдеудің барлық түбірлері жиыны екі саннан тұрады: x 1 =2 және x 2 =-2. -2 саны бірінші теңдеудің ММО-на кірмейді, сондықтан оның түбірі бола алмайды; демек бұл теңдеулер тең күшті емес.
Мысал 9. 2
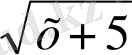 =x+2 және 4(x+5) =(x+2)
2
теңдеулері тең күшті бола ма?
=x+2 және 4(x+5) =(x+2)
2
теңдеулері тең күшті бола ма?
Шешуі. Екінші теңдеудің барлық түбірлері жиыны 4 және -4 екі санынан тұрады. Бірақ -4 саны бірінші теңдеудің түбірі болып табылмайды; сондықтан берілген теңдеулер тең күшті болып табылмайды. Бұнда -4 саны х
 -5 шартын қанағаттандырады, яғни бірінші теңдеудің ММО-на кіреді: демек бұл теңдеулер бірінші теңдеудің ММО-да тең күшті болып табылмайды. Олар, мысалы х
-5 шартын қанағаттандырады, яғни бірінші теңдеудің ММО-на кіреді: демек бұл теңдеулер бірінші теңдеудің ММО-да тең күшті болып табылмайды. Олар, мысалы х
 -2 жиынында тең күшті, өйткені бұл жиында 4 саны бірінші теңдеудің де, екінші теңдеудің де жалғыз түбірі болып табылады.
-2 жиынында тең күшті, өйткені бұл жиында 4 саны бірінші теңдеудің де, екінші теңдеудің де жалғыз түбірі болып табылады.
Модулі бар теңдеулер
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz