Сандар ұғымы және арифметикалық қасиеттері: разрядтар, амалдар, бөлгіштік, бөлшектер, пропорциялар және пайыздар


1. САНДАР ҰҒЫМЫ.
Математиканың негізі- сандар. Математиканы үйренуді сандар ұғымын түсінуден бастаған жөн.
Адамдар жекелеген нәрселерді санауда натурал сандары қолдана бастады.
Оларды жазу үшін арнайы таңбалар - цифралар пайдаланылды.
Цифралар 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Натурал сандар жиыны: N={1. 2. 3…. . }
Натурал сандары разрядтық қосылғыштарға жіктеуге болады.
Мысалы: 543=500+40+3=5*100+4*10+3
Санның жазылуында 3-бірілік, 4-ондық, 5-жүздік разрядтары бар.
Жалпы түрде, бес таңбалы санды abcde деп жазып, разрядтық қосылғыштарға төмендегідей жіктеуге болады:
а* 1+b*1000+c*100+d*10+e
немесе
а*10 4 +b*10 3 +с*10 2 +d*10 1 +e*10 0
Анықтама: Қосындысы нольге тең екі санды қарама-қарсы сандар деп атайды.
7+(-7) =0 Болғандықтан 7 және -7 қарама қарсы сандар.
Мысалы: 18 және -18 ; -4/17 және 4/17;
-0, 43 және 0, 43;
Анықтама: Барлық натурал сандар мен оларға қарсы сандары және 0-ді бүтін сандар жиыны деп атайды.
Z={…-3, -2, -1, 0, 1, 2, 3…}
0-саны оң санға да, теріс санға да, жатпайды. Бүтін сандарды қосуға, азайтуға, көбейтуге, бөлуге болады.
Мысалы:
- 6+5=11, Мұндағы 6; 5 сандары - қосылғыштар, 11- қосынды.
- 18-3=15, 18-азайғыш, 3-азайтқыш, 15-айырма.
- 8*9=72, 8; 9 сандары- көбейткіштер, 72- көбейтінді
- 24:4=6; 24-бөлінгіш, 4-бөлгіш, 6-бөлінді.
Қосу мен азайтудың амалдарын- бірінші басқыш амалдары деп атайды.
Көбейту мен бөлуді- екінші басқыш амалдары деп атайды.
Амалдардың орындалу тәртібі.
- Егер санды өрнек тек бірінші басқыш амалдарынан тұрса, амалдар солдан оңға қарай ретімен орындалады.
- Егер санды өрнекте барлық амалдар кездессе, онда алдымен екінші басқыш амалдары, содан кейын бірінші басқыш амалдары орындалады.
- Егер санды өрнекте жақшалар болса, онда бірінші кезекте жақшаның ішіндегі амалдар жоғарыдағы екі тұжырымдамаға сәйкес орындалады. Жақшаның ішіндегі амалдар орындалып біткен соң, сыртындағы амалдар орындалады.
Мысалы: (28*93+(1927-1873) *31) :6-710
Амалдардың орындалу ретін көрсетсек:
Шешуі: 1 амал 1927-1873=54
2 амал 54*31=1674
3 амал 28*93=2604
4 амал 2604+1674=4278
5 амал 4278:6=713
6 амал 713-710=3 Жауабы: 3
- ҚОСУ МЕН КӨБЕЙТУДІҢ ЗАҢДАРЫ.
- Ауыстырымдылық заңы:
a+b=b+a
a
\[\stackrel{\Phi}{\sim}\]b=b\[\stackrel{\Phi}{\sim}\]а
- Терімділік заңы:
(a+b) +c=a+(b+c) =(a+c) +b
(a
\[\stackrel{\Phi}{\sim}\]b)\[\Phi\]c=a(a\[\stackrel{\Phi}{\sim}\]c)\[\stackrel{\Phi}{\sim}\]b
3. Көбейтудің үлестірімділік заңы:
a (b+c) =ab+ac
Бұл заңдары ретімен орынды қолдану арқылы есептеуді жеңілдетуге болады
Мысалы:
а) 78
ә)
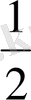 +6
+6

- САНДАРДЫҢ БӨЛГІШТЕРІ МЕН ЕСЕЛІКТЕРІ
Анықтама: а санының бөлгіші деп а санын қалдықсыз бөлетін санды айтады.
Мысалы: 18 санының бөлгіштері: 1, 2, 3, 6, 9, 18
Бөлшектер саны шектеулі болады.
Анықтама: а санының еселігі деп а санына қалдықсыз бөлінетін санды айтады. Мысалы 5-тің еселіктері 0, 5, 10, . . . Еселіктер саны шексіз.
Санды қалдықпен бөлу.
Егерде қандайда бір m санын n-ге бөлгенде бүтіндей бөлінбесе, онда оны қалдықпен бөлу деп атайды.
Мысалы: 25 6
24
 4
4
1 қалдық
онда 25=4
Жалпы түрде, m=n
- САНДАРДЫҢ БӨЛІНГІШТІК БЕЛГІЛЕРІ.
Бөлгіншілік белгілері қосынды мен көбейтіндінің қасиеттеріне негізделген.
1. Егер әрбір қосылғыш қандай да бір санға бөлінсе, онда қосынды да сол санға бөлінеді.
Мысалы :
(15+30) :3=15:3+30:3=5+10
2. Егер қосылғыштардың біреуі қандай да бір санға бөлінбесе, онда қосынды да сол санға бөлінбейді.
(7+14) :2 берілсе, 7 саны 2-ге бөленбейді, олай болса, қосынды21-де 2-ге бөлінбейді.
3. Егер азайғыш және азайтқыш қандай да бір санға бөлінсе, онда айырма сол санға бөлінеді.
Мысалы :
(100-70) :10=100:10-70:10=10-7 яғни 100-70=30. 30:10=3
4. Егер бір санға азайғыш бөлінбесе, ал азайтқыш бөлінсе, онда айырма сол санға бөлінбейді.
Мысалы :
(47-25) :5 өрнегінде 47 саны 5-ке бөлінбейді. 25-саны 5-ке бөлінеді, сондықтан 47-25=22 айырмасында 5-ке бөлінбейді.
5. Егер көбейткіштердің ең болмағанда біреуі қандайда бір санға бөлінсе, онда көбейтінді де сол санға бөлінеді.
Мысалы : 15
а. 2 санына бөлінгіштік белгісі.
Натурал сандар жұп және тақ сандар деп бөлінеді. Жұп сандарының сонғы цифралары 0, 2, 4, 6, 8 болды.
Мысалы: 50, 102, 46, 78, 94. Тақ сандардың соңғы цифрлары 1, 3, 5, 7, 9 болады
Мысалы : 41, 83, 105, 17, 29
Жұп сандар 2-ге бөлінеді.
Жұп сандардың формуласын 2n деп, тақ сандардың 2n-1 немесе 2n+1 деп көрсетуге болады.
Мысалы : 24=2
17=2
29=2
b. 5 санына бөлінгіштік белгісі. 0 және 5 цифраларымен аяқталған сандар 5 ке бөлінеді. Мысалы : 45, 210, 1925, . . .
с. 10-ға бөлінгіштік белгісі.
0 мен аяқталған сандар 10-ға бөлінеді.
Мысалы : 50, 700, 430
d. 3-ке және 9-ға бөлінгіштік белгілері.
Берілген санның цифрларының қосындысы 3-ке (9-ға) бөлінсе, ол санның өзі де 3-ке (9-ға) бөлінеді, егер санның цифрларының қосындысы 3-ке (9-ға) бөлінбесе, онда ол сан 3-ке (9-ға) бөлінбейді.
Мысалы : а) 654саны 3-ке, 9-ға бөлінетінін анықтайық:
Шешуі: Ол үшін санның цифрларының қосындысын табамыз.
6+5+4=15 ; 15:3=5, онда 654 саны 3-ке бөлінеді.
15саны 9-ға бөлінбейді, сондықтан 654 саны да 9-ға бөлінбейді.
б) 3485* санының жазылуындағы жұлдызшаның орнына тиісті цифрларды қойып, а) 3- ке еселік
б) 9-ға еселік сандарды жазыңыз.
Шешуі: Саның жазылуындағы цифрлардың толық емес қосындысын табайық: 3+4+8+5=20
Берілген сан 3-ке бөлінуі үшін қосынды 21, 24, 27 болуы қажет, сондықтан жұлдызшаның орнына 1, 4, 7 цифрларын қоюға болады.
Берілген сан 9-ға бөлінуі үшін қосынды 27 болу керек, сондықтан жұлдызшаның орнына 7 цифрын жазамыз.
е. 4-ке бөлінгіштік белгісі.
Егер үш таңбалы санның соңғы екі цифрымен жасалған екі таңбалы сан 4-ке бөлінсе, берілген санның өзі де 4-ке бөлінеді.
Мысалы: 5036саны 4-ке бөлінеді, себебі санның соңғы цифрымен жасалған сан 36саны 4-ке бөлінеді.
f. 11-ге бөлінгіштік белгісі
Натурал санның жазылуындағы жұп орындағы цифрлардың қосындысы мен тақ орындағы цифрлардың қосындысының айырмасы 11-ге бөлінсе, онда берілген сан да 11-ге бөлінеді.
Мысалы : а) 253 санының 11-ге бөлінетін анықтайық.
Шешуі: тақ, және жұп орында тұрған цифрлардың қосындысын есептейк.
2+3=5; жұп орында тек 5 цифры тұр.
5-5=0; 0 саны 11-ге бөлінеді. Олай болса, 253 саны 11-ге бөлінеді.
б) 748 санының 11-ге бөлінетінің тексерейік.
Шешуі: жұп орында тұрған цифрлардың қосындысы 4.
Тақ орында тұрған цифрлардың қосындысы 7+8=15. Айырма: 15-4=11 11 өзіне бөлінеді, онда 748 саны да 11-ге бөлінеді.
Мысалы : в) 237849568
Тақ орында тұрған цифрлардың қосындысын есептесек:
2+7+4+5+8=26 болады
Жұп орында тұрған цифрлардың қосындысы
3+8+9+6=26-ға тең .
Екі қосындысының айырмасы 26-26=0. 0 саны 11-ге бөлінеді. Олай болса, берілген санның өзі де 11-ге бөлінеді.
g. 7-ге, 13-ке бөлінгіштің белгілері.
Берілген натурал сан 7-ге (13-ке) бөлінетінің тексеру үшін сол санның цифрларын оңнан солға қарай 3 цифрдан топтаймыз немесе бір цифрда болуы мүмкін.
Тақ нөмірлі топтарды плюс таңбасы мен, жұп нөмірлі топтарды минус таңбасымен жазып, өрнек кұрамыз. Сол өрнектің мәні 7-ге (13-ке) бөлінсе, онда берілген санның өзі де 7-ге (13-ке) бөлінеді.
Мысалы : а) 1809227 санының 7-ге (13-ке) бөлінуін анықтайық.
Тақ нөмірлі топтар: 180 және 7.
Жұп нөмірлі топ: 922
б) 659865024 санының 7-ге және 13-ке бөлінетінің тексерейік.
Шешуі: Тақ нөмірлі топтар: 659 және 024.
Жұп нөмірлі топтар: 865.
Өрнектің мәнін есептейік:
180-922+7=-735
735 саны 7-ге бөлінеді, олай болса, берілген санның өзі де 7-ге бөлінеді
h. 25-ке бөлінгіштік белгісі.
Көп таңбалы санның жазылуындағы соңғы екі цифрмен жазылған сан 25-ке бөлінсе, онда берілген санның өзі де 25-ке бөлінеді.
Мысалы : 42175 саны 25-ке бөлінеді, себебі санның соңғы екі цифрымен жасалған 75 саны 25-ке бөлінеді.
1. 4. ЖАЙ ЖӘНЕ ҚҰРАМА САНДАР.
Анықтама: 1-ге және өзіне ғана бөлінетін сандарды жай сандар деп атайды.
Жай сандардың кестесі
Анықтама: Бөлгіштерінің саны екіден артық болса, ол санды құрама сан деп атайды.
Мысалы : 12- құрама сан
12-нің бөлгіштері: 1, 2, 34, 6, 12.
 Анықтама:
Егер екі санның ортақ бөлгіші тек 1 саны ғана болса, онда екі санды өзара
жай сандар
деп атайды.
Анықтама:
Егер екі санның ортақ бөлгіші тек 1 саны ғана болса, онда екі санды өзара
жай сандар
деп атайды.
Мысалы : 9және 8; 25 және 16.
- САНДАРДЫ ЖАЙ КӨБЕЙТКІШТЕРГЕ ЖІКТЕУ.
Кез келген құрама санды жай сандардың көбейтіндісі түрінде жазуға болады.
Мысалы : 12=2
Сондарды жіктеуді былай жазған қолайлы:
48 2
24 2
12 2 48=2 4
6 2
3 3
1
а. Екі санның ең үлкен ортақ бөлгішін табу.
Қысқаша белгілеу Е. Y. O. Б (а, в)
Анықтама: Екі санның ең үлкен ортақ бөлгішін табу үшін :
- берілген сандарды жай
көбейткіштерге жіктейміз;
- шыққан жіктеулердегі барлық ортақ
жай көбейткіштерді табамыз;
- ортақ көбейткіштердің көбейтіндісін табамыз;
Мысалы : Е. Y. O. Б (630, 252) =табайық.
Екі санды жай көбейткіштерге жіктейміз:
252 2 630 2
126 2 315 3
63 3 105 3
21 3 35 5
7 7 7 7
1 1
Е. Y. O. Б (630, 252) =2
b. Екі санның ең кіші ортақ еселігін табу.
Қысқаша белгілеуі: Е. К. О. Е. (а, в)
Анықтама: Екі натурал санның ең кіші ортақ еселігі деп берілген сандардың әр қайсысына бөлінетін ең кіші натурал санды айтады.
Екі санның ең кіші ортақ еселігін табу үшін:
- берілген сандарды жай көбейткіштерге жіктейміз;
- жіктелудің біріншісінде жоқ көбейткіштерді екінші жіктелудегі көбейткіштерімен толықтыру керек;
- шыққан көбейткіштердің көбейтіндісін есептеп шығарамыз;
Мысалы : а) Е. К. О. Е. (18, 42) =?
Шешуі: 18 2 18=2
9 3 21 3
3 3 7 7
1 1
Е. К. О. Е. (18, 42) =2
\[\stackrel{\Phi}{\sim}\]3\[\Phi\]3\[\stackrel{\Phi}{\sim}\]7=126
б) Е. К. О. Е. (54, 72) =?
54 2 54=2
27 3 36 2
9 3 18 2
3 3 9 3
1 3 3
1
Е. К. О. Е. ( 54, 72) =2 3
\[\stackrel{\Phi}{\sim}\]3 3 =216
в) Е. К. О. Е. ( 462; 420) -ін табайық
462 2 462= 2
231 3 210 2
77 7 105 3
11 11 35 5
1 7 7
1
Е. К. О. Е. (462, 420) = 2
Жай бөлшектерді қысқарту үшін бөлшектің алымы мен бөліміндегі сандардың Е. Ү. О. Б. -ін табамыз.
Мысалы : 36/54 бөлшегін қысқарту керек:
Е. Ү. О. Б. (36, 54) =18
1. 6 ЕВКЛИД АЛГОРИТМІ.
Өте үлкен екі санның ең үлкен ортақ бөлгішін іздеу үшін Евклид алгоритмін қолдануға болады.
Тұжырымдама: Егер а, в- натурал сандар және а саны в-ға бөлінетін болса, онда а саны мен в-ның ортақ бөлгіші в саны болады.
Мысалы : 24және 8; 24 саны 8-ге бөлінеді. Олай болса, Е. Ү. О. Б. (24, 8) =8
Тұжырымдама: Егер а және в натурал сандар және а>b болса, онда а мен в -ның ортақ бөлгіші а-в мен в- ның ортақ бөлгішіне тең, немесе а санның в санына қалдықпен бөлгендегі ең соңғы нольден өзгеше қалдық берілген екі санның ортақ бөлгіші болады.
Мысалы : а) О. Б. (2304; 1296) =?
 2304 1296
2304 1296
1296 1
1296 1008
1008 1
1008 288
864 3
288 144
288 2
0 О. Б. (2304, 1296) =144
б) О. Б. (7975, 2585) =ін табу керек
 7975 2585
7975 2585
7755 3
2585 220
2420 11
220 165
165 1
165 55
165 3
0
О. Б. (7975, 2585) =55
Өзара жай сандардың ең кіші ортақ еселігі осы сандардың қөбейтіндісі болады.
Мысалы : Е. К. О. Е. (4; 5; 7) =4
Қатар тұрған екі санның көбейтіндісі 2-ге, ал қатар үш санның көбейтіндісі 3-ке бөлінеді.
1. 7. ЖАЙ БӨЛШЕКТЕР.
m-алымы, n- бөлімі.
Жай бөлшектер дұрыс және бұрыс болып екіге бөлінеді.
Алымы бөлімінен кем болатын бөлшекті дұрыс бөлшек деп атайды.
 Мысалы
:
Мысалы
:
Алымы мен бөлімі тең немесе алымы бөлімінен артық бөлшекті бұрыс бөлшек деп атайды.
Мысалы :
Бұрыс бөлшекті натурал сан мен дұрыс бөлшектің қосындысы түрінде жазуға болады:
1)
2)
Мұндай түрде жазылған санды аралас сан деп атайды.
Аралас санды бұрыс бөлшекке айналдыру тәсілі:
а) 3
 =
=
а. Бөлшектің негізі қасиеті.
Бөлшектің алымы мен бөлімін бірдей санға көбейтуге немесе бөлуге болады. Бөлшектің алымы мен бөлімін бірдей санға бөлуді бөлшекті қысқарту деп атайды.
Бөлшекті қысқарту үшін алымы мен бөлімінде тұрған сандардың ең үлкен ортақ бөлгіші табылады.
Мысалы : 114/171 бөлшегін қысқарту керек.
Е. К. О. Е (144, 171) =3
144 2 171 3
57 3 57 3
19 19 19 19
1 1
b. Жай бөлшектермен амалдар орындау.
1. Бөлімдері бірдей бөлшектерді қосу және азайту
а)
2. Бөлімдері әр түрлі бөлшектерді қосу және азайту
а) 6
18 2 21 3
9 3 7 7 Е. К. О. Е. (18. 21) =2
3 3 1
1
б) 9
15 3 36 2 Е. К. О. Е. (15. 36) =180
5 5 18 2
1 9 3
3 3
1
3. Бөлшектерді көбейту.
а) 2
\[\frac{\prod}{\bigotimes}\]\[\stackrel{\Phi}{\sim}\]1\[\frac{1}{17}\]=\[\frac{2\cdot8+1}{8}\]\[\stackrel{\Phi}{\sim}\]\[\frac{1\cdot17+1}{17}\]=\[\frac{17}{8}\]\[\stackrel{\Phi}{\to}\]\[\frac{18}{17}\]=\[\frac{\mathbb{Q}}{\langle\mathbb{Q}\rangle}\]= 2\[\frac{\rfloor}{\longrightarrow}\]б) 7
\[\frac{5}{12}\]\[\stackrel{\Phi}{\sim}\]4=\[\frac{7\cdot12+5}{12}\]\[\stackrel{\Phi}{\sim}\]\[\frac{d}{\textsf{I}}\]=\[\frac{89}{12}\]\[\stackrel{\Phi}{\sim}\]\[\frac{{\mathcal{A}}}{\prod}\]=\[\frac{89}{3}\]= 29\[\frac{\mathcal{N}}{\sim}\]в)
\[\frac{\alpha}{\mathrm{e}}\frac{5}{7}\frac{\mathrm{e}^{2}}{\phi}\]\[\Phi\]\[\frac{14}{19}\]=\[\operatorname{slo}{\hat{\vec{x}}}\]\[\stackrel{\Phi}{\sim}\]\[\frac{14}{19}\]=\[\frac{19}{7}\]\[\stackrel{\Phi}{\sim}\]\[\frac{19}{7}\]\[\stackrel{\Phi}{\sim}\]\[\frac{14}{19}\]=\[\frac{19\cdot19\cdot14^{2}}{7\cdot7\cdot19_{1}}\]=\[\frac{38}{7}\]= 5\[\frac{\mathcal{N}}{\mathcal{D}}\]
4. Бөлшектерді бөлу.
Анықтама: Көбейтіндісі 1-ге тең екі санды кері сандар деп атайды.
2 және
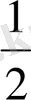 ;
;
Бөлшекті бөлшекке бөлу үшін берілген бөлшекті екінші бөлшекке кері санмен көбейту:
а) 7

б)
в)
 85
85
1. 8. ОНДЫҚ БӨЛШЕКТЕР.
Анықтама: Бөлімдері бір мен нольден тұратын бөлшекті ондық бөлшек деп атайды.
.
Ондық бөлшекпен амалдар.
1. Қосу: 12, 043+5, 9=12, 043
+ 5, 900
17, 943
2. Азайту: 7, 1-2, 958=7, 100
- 2, 958
4, 142
3. Көбейту: 2, 07
х 3, 5
1035
+ 621
7, 245
4. Бөлу: 1, 75 2, 5
- 0 0, 7
175
175
0
Амалдарды орындау ережесін есіңізге сақтаңыз.
- Ондық бөлшекті қосу (азайту) үшін:
а) бұл бөлшектердің үтірден кейінгі таңбаларының санын теңестеру керек;
ә) үтірдің астына үтір тура келетіндей етіп, оларды бірінің астына бірін келтіріп жазу керек;
б) үтірге көңіл бөлмей қосуды (азайтуды) орындау керек;
в) шыққан жауапта үтірді берілген бөлшектердегі үтірдің астына келтіріп қою керек.
2) Онық бөлшектерді көбейту үшін:
а) үтірге назар аудармай көбейтуді орындау керек;
ә) екі көбейткіште де үтірден кейін қанша цифр тұрса, сонша цифрды оң жақтан үтірмен айырып бөлу керек. Егер көбейтіндідегі цифрлар үтірмен айырылуға тиісті цифрлардан аз болса, онда көбейтіндінің алдынан бір немесе бірнеше ноль жазылады.
3) Сады ондық бөлшекке бөлу үшін:
а) бөлгіште үтірден кейін қанша цифр тұрса, бөлінгіш пен бөлгіштегі үтірді оңға қарай сонша цифр аттап көшіру керек;
ә) сонан кейін натурал санға бөлуді орындау керек.
Математика, физика, химия есептерін шығарғанда сандардың жуық мәндері кездеседі.
Егер а<x<b болса, онда а саннын x-тің кемімен алынған жуық мәні, ал b саннын x-тің артығымен алынған жуық мәні деп атайды.
Мысалы : 2, 8<x<2. 9 болса, x
Анықтама: Санды оған жақынырақ натурал санмен немесе нольмен алмастыруды осы санды бүтінге дейін дөңгелектеу деп атайды.
Ереже: Егер санды қандай да бір разрядқа дейін дөңгелектейтін болса, ол разрядтан кейінгі келесі цифрлардың барлығын нольдермен алмастырады, ал ол цифрлар үтірден кейін тұрса, оларды алып тастайды. Егер алып тастаған немесе нольмен алмастырылған бірінші цифр 5, 6, 7, 8, немесе 9-ға тең болса, онда алдындағы цифрға 1-ді қосады. Егер алып тастаған немесе бірінші нольмен алмастырылған бірінші цифр 0, 1, 2, 3 немесе 3-ке тең болса, онда оның алдында тұратын санды өзгертпей қалдырады.
14, 25
1, 35506
1. 9. РАЦИОНАЛ САНДАР.
Анықтама: Бүтін сандарды бөлшектермен біріктіріп рационал сандар жиыны деп атайды.
Белгілеуі: Q
Кез келген рационал санды
Q= {
Мысалы : 5=
1. 10. САННЫҢ МОДУЛІ.
Анықтама: Санақ басынан санды кескіндейтін нүктеге дейінгі қашықтық модуль немесе санның абсолют мәні (абсолют шамасы) деп аталады. Сонымен, оң санның өзі, ал теріс санның модулі оған қарама-қарсы сан болады.
Белгілеуі:
Мысалы:
Рационал сандарға қолданылатын амалдар.
1. Екі теріс санның қосындысы - теріс сан.
а) қосылғыштардың модульдерін қосып аламыз;
б) шыққан нәтиженің алдына « - » таңбасын қою керек. -18+(-23) = -41
2. Таңбалары әр түрлі сандарды қосу үшін:
а) үлкен модульден кіші модульді азайту керек;
б) сонда шыққан санның алдына модулі үлкен қосылғыштың таңбасын қою керек.
Мысалы: 1) -7+9=2; 2) 7+(-9) =-2
Таңбалары әр түрлі бірнеше санды қосқанда, қарама-қарсы сандар болса сызып тастаймыз. Содан кейін таңбалары бірдей сандарды топтаймыз.
Мысалы: -9+(-5) +10+(-3) +(-7) +9+(-8) +1+2=10+1+2+(-5) +(-3) +(-7) +(-8) =13+ (-23) =-10
3. Рационал сандарды азайтуды қосумен алмастырған жөн.
Мысалы: 1) 5-8=5+(-8) =-3; 2) -10-2=-10+(-2) =-12
4. Екі теріс санды көбейткенде, бөлгенде, оң сан шығады.
Мысалы: -27
5. Таңбалары әр түрлі екі санды бөлгенде, көбейткенде, нәтижеде теріс сан болады. Мысалы: 8
Жай бөлшекті ондық бөлшекке айналдыру.
1)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz