Бөлшек рационал өрнектер

Алгебралық өрнектерді түрлендіру
1. Дәреже
Анықтама: Бірдей көрсеткіштердің көбейтіндісін дәреже деп атайды.
а ٠а•...•a=an

an өрнегі – дәреже, a – дәреженің негізі, n – дәреже көрсеткіші деп
аталады.
Дәреженің нәтижесін табу амалын дәрежелеу деп атайды.
а2 өрнегін а – ның квадраты, а3 өрнегін а – ның кубы деп атайды.
Егер n=1 болса, a1=a сондықтан 1 дәреже көрсеткіші жазылмайды. Негізгі оң
санды дәрежелегенде, оң сан шығады.
Мысалы: 63 =6*6*6=216

Негізгі теріс санды жұп дәрежеге шығарғанда, оң сан шығады.
(-2)4 = (-2)*(-2)*(-2)*(-2)=16

Негізгі теріс санды тақ дәрежеге шығарғанда, нәтижеде теріс сан шығады.
(-3)3 = (-3)*(-3)*(-3)=-27

Дәреженің қасиеттері
1. an *am = an+m
Мысалы: 34 *35 = 34+5=39
2. 2. an ÷am = an /am = an-m
Мысалы: 27 *22 = 27/22=27-2=25
3. (an)m=anm
Мысалы: (52)3 = 52*3=56
4. (a*b)n=an *bn
Мысалы: (2 *3)3 = 23*33
5. (a/b)n = an/bn
Мысалы: (3 /4 )2= 32/42
6. a0=1
Мысалы: 90=1

Егер а≠0 және рационал сан болсын
а-n=1/an
Мысалы: 7-2=1/72 =1/49
Салдар (a/b)-n=(b/a)n
Мысалы: а) (4/3)-3 = (3/4)3=33/43 = 27/64

б) ( 1 2/3 )-2 = (5/3)-2 = (3/5)2 = 33/53=9/25

2. Санның стандарт түрі
Анықтама: а- оң саны а1 * 10n түрінде жазылса, ол өрнек а – ның стандарт
түрде жазылуы деп аталады, мұндағы 1≤а1<10, n – бүтін сан. n – санын
берілген санның реті деп атайды.
Мысалы: 1. 2947=2.947 * 103
2. 0.000918=9.18 * 10-4

Стандарт түрде жазылған сандармен амалдар орындауға болады.
Мысалы:
1. (5,1 * 104) * (1,3 * 103)=5,1 * 1,3 * 104+3=6,63 * 10 7
2. (5,4 * 105) ׃ (1,5 * 10-6)=(5,4 ׃ 1,5) * 105-(-6)=3,6 * 1011

1.2. Арифметикалық түбір ұғымы
Арифметикалық түбірдің қасиеттері
Анықтама: а нақты санының n – ші дәрежелі түбірі деп, n- ші дәрежесі а-
ға тең санды айтады.
Белгілеуі: 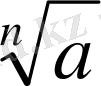, мұндағы n және n≠1
n – түбірдің көрсеткіші
а – түбір астындағы өрнек
Анықтама бойынша
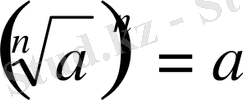
Мысалы: 32 санының 5-дәрежелі түбірі 2 саны.
Жазылуы: себебі 25=32
n = 2 болғанда а – ның түбірі өрнегімен жазылып, квадрат түбір
деп аталады. Түбірді «радикал» терминімен ауыстыруға болады.

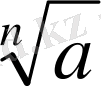
Мысалы: 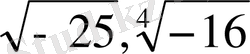өрнектерінің мағынасы жоқ.
Жұп көрсеткішті түбірдің мағынасы болу үшін, түбір астындағы өрнек
теріс емес мәнді қабылдауы керек.
Мысалы: функциясының анықталу облысын табыңыз.
Шешуі: 6-х≥0 болу керек.
-х≥-6 теңсіздіктің екі бөлігін - 1 санына көбейтсек,
х≤6 х (-∞;6]
Жауабы: (-∞;6]

n - жұп сан, а >0 болғанда 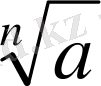өрнегінің екі мәні болады.
Мысалы: 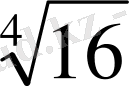=2 және 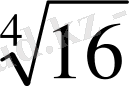=-2

Анықтама: 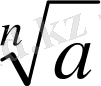өрнегінің (n - жұп сан) арифметикалық түбірі деп n -
дәрежесі а – ға тең теріс емес санды айтады.
Мысалы:
1) өрнегінің арифметикалық түбірі 3.
2) Егер х4 =81 теңдеуін шешкенде, х = ± деп, х1 =-3; x2 = 3 екі
түбірін де жазу керек.
3) х2 – 5 =0 теңдеуін шешіңіз.
Шешуі: х2= 5 х =± яғни х1 =-; x2 =
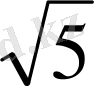
4) х4 + 4/25=0 теңдеуін шешіңіз.
х4 =- 4/25 х= өрнегінің мағынасы жоқ, сондықтан берілген
теңдеудің шешімі де болмайды. n тақ сан болғанда, өрнегінің а-ның
кез келген мәнінде мағынасы болады.
Мысалы: 1)
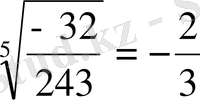
2) Теңдеуді шешіңіз: х7 + 15 =0
Шешуі: х7 =-15 х = - немесе х =
Түбірдің қасиеттері
1.
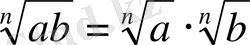
Мысалы:
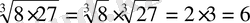
2.
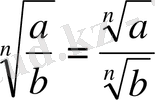
Мысалы:
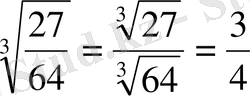
3.
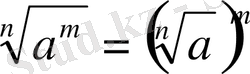
Мысалы:
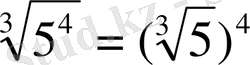
4.
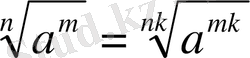
Мысалы:
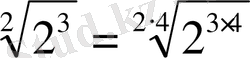
5.
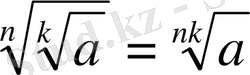
Мысалы:

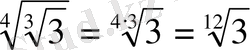
Квадрат түбірлер үшін негізгі теңбе – теңдіктер
1.
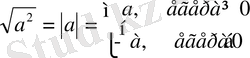
Мысалы: =6
2. болса
Мысалы: Ықшамдаңыз:

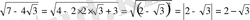
Себебі

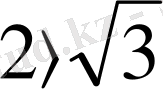
Бөлщек көрсеткішті дәреже
Анықтама: а≥0, m,n – натурал сандар болса,
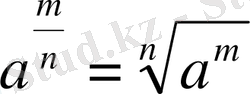
Мысалы:
1)
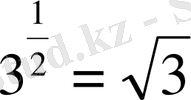
2)
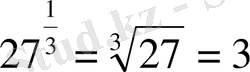
3)
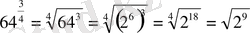
4) есептеңіз:

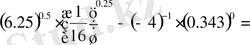
Шешуі:
1.
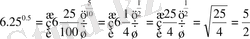
2.
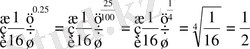
3.
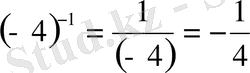
4. олай болса,

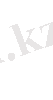
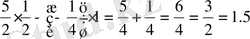
Жауабы: 1,5

Түбірлері бар өрнектерді түрлендіру мысалдары
1) Өрнекті ықшамдаңыз:

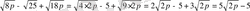
2) Өрнекті түрлендіріңіз:
3) Бөлшекті қысқартыңыз:
4) Бөлшектің бөліміндегі иррационалдықтан арылыңыз:
а)
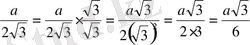
б)
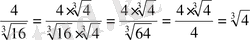
в)
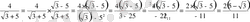
Бөлшектің алымындағы иррационалдықтан арылыңыз:
г)
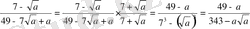
5) Сандарды салыстырыңыз:
а)

1)
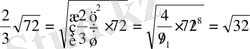
2)
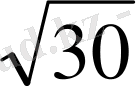
3) 30<32<98 олай болса,
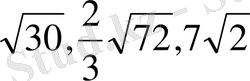
б) Өсу ретімен орналастырыңыз:
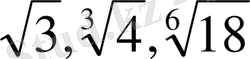
Түбірдің көрсеткіштерін бірдей етіп аламыз.
1)
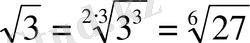
2)
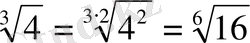
3) 16<18<27 болғандықтан

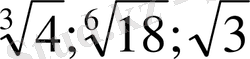
6)

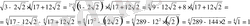
Квадрат түбірлері бар есептерді шығарғанда
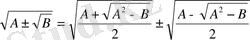
формуласын да пайдалануға болады.
Мысалы: Өрнекті ықшамдаңыз.
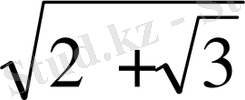
1 – тәсіл: А=2;B=3
2 – тәсіл: 2+ өрнегін екі мүшенің қосындысының квадраты түрінде
жазамыз.

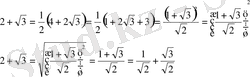
1.3. Алгебралық өрнектердің түрлері туралы негізгі ұғымдар

1. Анықтама: Сандар мен айнымалылардан қосу, азайту, көбейту, бөлу,
дәрежелеу және түбір табу амалдары арқылы жасалған өрнектерді алгебралық
өрнектер деп атайды.

Мысалы:
1)
2) 3
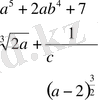
3)

2. Анықтама: Алгебралық өрнекте айнымалыға бөлу амалы болмаса, ол өрнек
бүтін деп аталады.
Мысалы:
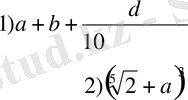
3. Анықтама: Құрамында айнымалыға бөлу амалы бар алгебралық өрнекті бөлшек
алгебралық өрнек деп атайды.

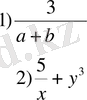
4. Анықтама: Бүтін және бөлшек өрнектерді біріктіріп, рационал өрнектер
деп атайды.
5. Анықтама: алгебралық өрнектің құрамында айнымалыдан түбір табу немесе
айнымалының бөлшек көрсеткішті дәрежесі болса, ондай өрнекті иррационал
өрнек деп атайды.
Мысалы:
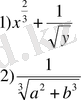
Анықтама: Айнымалылардың алгебралық өрнекке мағына беретін мәндерін
айнымалының мүмкін мәндері деп атайды.
Анықтама: Айнымалының мүмкін мәндерінің жиынын алгебралық өрнектің анықталу
облысы деп атайды.
Бүтін өрнектің айнымалының кез келген мәнінде мағынасы болады.
Бөлшек алгебралық өрнектің мағынасы болу үшін, бөлшектің бөліміндегі
өрнектің мәні нольге тең болмау керек.
Мысалы:Өрнектің анықталу облысын табыңыз.
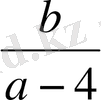
Шешуі:
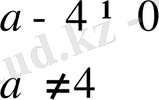
Жауабы: немесе

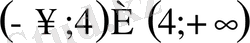
Иррационал алгебралық өрнекте түбір көрсеткіші жұп сан болса, онда түбір
астындағы өрнектің мәні теріс сан болмау керек.
Мысалы: Өрнектің анықталу облысын табыңыз.
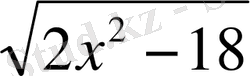
Шешуі:

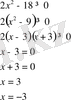
Жауабы: және немесе

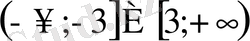
Анықтама: Алгебралық өрнекке айнымалылардың мүмкін мәндерін қойып,
өрнектегі амалдарды орындағаннан кейін шыққан нәтижені алгебралық
өрнектің мәні деп атайды.

Мысалы: өрнегін ықшамдап, х=-2,5 болғандағы мәнін табыңыз.
Шешуі:
Жауабы: 20

1.4. Бүтін рационал өрнектер

1. Бірмүшелер және оларға амалдар қолдану
Анықтама: Сандар мен айнымалылардың натурал көрсеткішті дәрежелерінің
көбейтіндісінен тұратын өрнекті бірмүше деп атайды.
Мысалы:

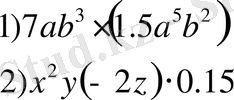
Құрамындағы сандарды бір-біріне көбейтіп, бірдей негізді айнымалылардың
дәреже көрсеткіштерін қосып ықшамдаңыз. Сан көбейткіш алдына жазылады
және коэффициент деп аталады. Бірмүшенің ықшамдалған түрін оның стандарт
түрі деп атайды. Бірмүшенің дәрежесі деп оның құрамындағы айнымалылардың
дәреже көрсеткіштерінің қосындысын айтады.
Мысалы:
1) Бірмүшені стандарт түрде жазып және дәрежесін анықтаңыз:

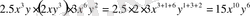
Бірмүшенің дәрежесі 10+6= 16-ға тең.
2) бірмүшені үшінші дәрежеге шығарыңыз:

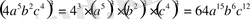
Құрамындағы айнымалылары және айнымалылардың дәреже көрсеткіштері
бірдей болатын мүшелер ұқсас мүшелер деп аталады.
Мысалы: және


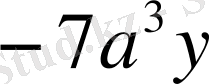
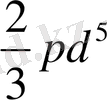
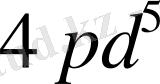
Ұқсас мүшелерді коэффициенттерінің таңбасын ескеріп бір – біріне қосады.
Мысалы:
Бірмүшелерді қосыңыз:

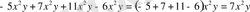
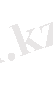
2.Көпмүше
Анықтама: Бірмүшелердің қосындысын көпмүше деп атайды.
Көпмүшенің дәрежесі деп оның құрамындағы бірмүшелердің дәрежесінің үлкенін
айтады.
Көпмүшенің ұқсас мүшелері біріктіріліп, реттеліп жазылған түрін оның
стандарт түрі деп атайды.
Айнымалысы жоқ мүшесін бос мүше деп атайды.
Мысалы: Көпмүшені стандарт түрге келтіріңіз:

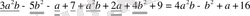
Үшінші дәрежелі көпмүше, бос мүшесі 16.

Жақшаны ашу ережесі
Көпмүшелерді қосқанда және азайтқанда жақшаларды ашу, топтау кезінде
жақшаға алу ережелерін білу қажет.
1. Егер жақшаның алдында «+» таңбасы болса онда жақшаны ашқанда оның
ішіндегі мүшелердің таңбасы өзгермейді.
Мысалы: 3х + (-4х +7)=3х – 4х +7 =-х+7
2. Егер жақшаның алдында «-» таңбасы тұрса, онда жақшаны ашқанда оның
ішіндегі мүшелердің таңбасы қарама – қарсы таңбаға өзгереді.
Мысалы: Өрнектерді жақшасыз жазып, ұқсас мүшелерін біріктіреміз.

(3х-4у)-(9х-7у)=3х-4у+9х+7у= -6х+3у
Көп мүшелерді жақшаға алғанда да осы ережені қолдану керек.
Мысалы: Көп мүшені көбейткіштерге жіктеңіз.
Ах +2а -3х -6=(ах+2а)-(3х+6)=а(х+2)-3(х+2)=(х+2)(а-3)

3. Қысқаша көбейту формулалары
1. (а+b)(a-b) = a2 – b2

Мысалы:
А)
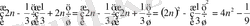
Б)
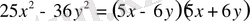
2. (а+b)2 = a2+2ab+b2
Мысалы:
А)
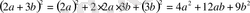
Б)
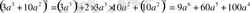
3. (a-b)2=a2-2ab+b2
Мысалы:
А)
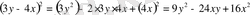
Б)
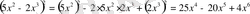
4. а3+b3=(a+b)(a2-ab+b2)
Мысалы:
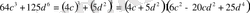
5. a3-b3 = (a-b)(a2+ab+b2)
Мысалы:

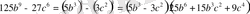
6. (a+b)3 =a3+3a2b+3ab2+b3
Мысалы:

7. (a-b)3 = a3-3a2b+3ab2-b3
Мысалы:

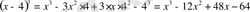
Үшмүшенің қосындысының квадраты үшін қысқаша көбейту формуласы:
(a+b+c)2 = a2 +b2+c2+2ab+2ac+2bc
Бөлшек көрсеткішті дәреже үшін қысқаша көбейту формулалары:
1.
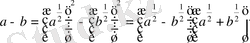
Мысалы:

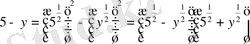
2 .=
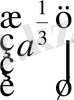
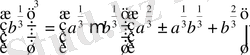
Мысалы:
2+c=

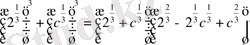
3. a

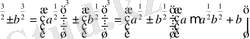
Мысалы:
3
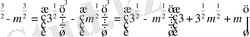
4. a
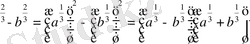
Мысалы:
7

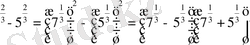
Тубірлері бар өрнектер үшін қысқаша көбейту формулалары.
1. a-b=

Мысалы:
2-c=
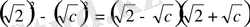
2. a

Мысалы: 2-c=
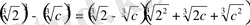
3. a
Мысалы: 3

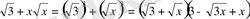
4 Көпмүшелерді көбейткіштеоге жіктеу
Анықтама: Көпмүшені бірмүше мен көпмүшенің немесе бірнеше көпмүшелердің
көбейтіндісі түрінде жазуды көпмүшені көбейткіштерге жіктеу деп атайды.
Көпмүшені көбейткіштерге жіктеудің бірнеше тәсілдері бар.
1. Ортақ көбейткішті жақшаның сыртына шығару тәсілі
Мысалы:
A) 6ac-4ab=2a(3c-2b)
12mn-15mn+30mn=3mn(4m-5n+10mn)
2.Қысқаша көбейту формулаларын қолдану тәсілі.
a) 25-n=5
б)
в) 36y
г)
3.Топтау тәсілі.
a) x
б) 20x3yz-15xy-4xz=
=
в) a-7ab+12b
-4b
г) x
=(x

1.19. Бөлшек рационал өрнектер.
түріндегі өрнек - бөлшек рационал өрнек, мұндағы P,
Q- рационал өрнектер.
Негізгі қасиеті: Бөлшек рационал өрнектің алымы мен бөлімін нольден
өзгеше бірмүшеге немесе көпмүшеге көбейтуге, бөлуге болады.
1.Рационал бөлшектерді қысқарту.
Рационал бөлшектерді қысқарту үшін алымы мен бөлімінің ортақ
көбейткішін анықтап соған алымын да , бөлімін де бөлу керек.
Мысалы: Бөлшекті қысқартыңыз:

3. Рационал бөлшектерді ортақ бөлімге келтіру.
1) Әрбір бөлшектің бөлімін көбейткіштерге жіктеу керек.
2) Ортақ бөлімін бөлшектін бөліміндегі әр түрлі көбейткіштердің
көбейтіндісінен құралады.Егер бірдей көбейткіштер кедессе, онда
олардың ішінен дәрежесінің үлкенін алады.
3) Әр бөлшекке толықтауыш көбейткіш береді. Ол үшін ортақ бөлімді
әр бөлшектің бөліміне бөлеміз.
4) Әрбір бөлшектің алымын толықтауыш көбейткіштерге көбейтеміз.

Мысалы: a) Бөлшектерді қосыңыз:

Е.К.О.Е.(4; 6;8)=24

б) Ықшамданыз:

Шешуі: Бөлшектің бөліміндегі өрнектерді жіктейміз.
2x+2x=2x
x-1=
Ортақ бөлімі: 2x(x-1)(x+1)
Жауабы:

=
4. Рационал бөлшектерді көбейту және бөлу.
Рационал бөлшектерді көбейту үшін екі бөлшектің алымдары
көбейтіліп
алымына , бөлімдері көбейтіліп бөліміне жазылады.

Мысалы: Бөлшектерді көбейтініз:

Рационал бөлшектерді бөлу үшін бірінші бөлшекті екінші бөлшекке
көбейту керек.

Мысалы:
=

4.Рационал бөлшекті дәрежеге шығару.

Мысалы:

1. 20. Иррационал өрнектер.
Иррационал өрнектерді түрлендіргенде арифметикалық түбірдің
қасиеттерін пайдаланамыз.
1. Ықшамданыз :
2.
3.
4. Көбейткішті түбір алдына шығарыңыз:
мұндағы b 0
Шешуі:

5. Бөлшекті қысқартыңыз.

Қарастырылған өрнектерден басқа трансцендентті өрнектерде болады.
Ол өрнектер көрсеткіштік, логарифмдік , тригонометриялық функциялармен
байланысты, сол тақырыптарды өткенде қарастырылады.
-----------------------
Ескерту: n жұп, а<0 болғанда өрнегінің мағынасы болмайды.