2014-2015 оқу жылы Республикалық математика олимпиадасының II кезеңі (9 және 11 сыныптар) - есептер мен толық шешімдер

Скачать

Математикадан Республикалық олимпиаданың ІІ кезеңі

2014 - 2015 оқу жылы

Амангелді Садыков

ШҚО Бородулиха ауданы Зубаир орта мектебінің математика пәнінің мұғалімі

Құрметті әріптестер! Олимпиадаларға дайындықты жалғастыруда оқушыларға көмегі болар деген мақсатпен биылғы жылғы олимпиада есептерінің шешулерін назарларыңызға ұсынып отырмын. Олимпиадаға дайындау барысында мүмкін кейбір есептердін әдемі тың шешімдерін табарсыздар деген ойдамын. Есептердің шешімдеріне байланысты оңды пікірлеріңізді білдірсеңіздер ризашылықпен қабылдаймын.

amangeldi. sadykov@mail. ru

9 сынып

1-тур

1. бесбұрышы шеңберге іштей сызылған. ∠CAD=50∘\angle CAD = 50^{{^\circ}}∠CAD=50∘\angle CAD = 50^{{^\circ}}екені белгілі. ∠ABC+∠AED\ \angle ABC + \angle AED∠ABC+∠AED\ \angle ABC + \angle AEDқосындысын табыңыз.
2. p(p+n) +p=(n+1) 3p(p + n) + p = (n + 1) ^{3}p(p+n) +p=(n+1) 3p(p + n) + p = (n + 1) ^{3}теңдігін қанағаттандыратынсаны табылатындай, барлық жайсандарын табыңыз.
3. 100+99+98+…+2+1<11\sqrt{100 + \sqrt{99 + \sqrt{98 + \ldots + \sqrt{2 + \sqrt{1 < 11100+99+98+…+2+1<11\sqrt{100 + \sqrt{99 + \sqrt{98 + \ldots + \sqrt{2 + \sqrt{1 < 11теңсіздігін дәлелдеңіз.

2 тур

4. Оқушылар емтихан тапсырғанда оларға 3 есеп берілді. Оқушылардың 98 % - бірінші, 90 % - екінші және 85 % - үшінші есепті шығарды. Барлық үш есепті оқушылардыңx%x\ \%x%x\ \%шығарды. - тің ең кіші және ең үлкен мәнін табыңыз.
5. Тіктөртбұрыш кестенің әрбір бірлік шаршысында нақты сан жазылған, және кестеде бірдей сан жоқ. Әрбір жолда ең үлкен сан таңдалған, - осы таңдалған сандардың ең кішісі. Әрбір бағанада ең кіші сан таңдалған, - осы таңдалған сандардың ең үлкені. жәнесаңдарын салыстырыңыз.
6. ішкі биссектрисасы ментөбесінің сыртқы қиылысады. сырттай сызылған шеңберBDBDBDBDтүзуін екінші ретнүктесінде қияды.

$E$ $E$ - $ACD$ $ACD$ үшбұрышына сырттай сызылған шеңбердің центрі екенін дәлелдеңіз.

9 сынып

І тур

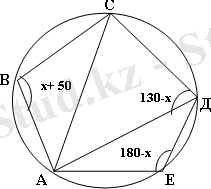1 Есеп . Шешуі:

1. ∆ АСД бойынша ∠ АСД = x, ∠ АДС = 130 - x
2. АСДЕ төртбұрышы шеңберге іштей сызылған, ендеше бұл төртбұрыш бойынша

∠ АЕД = 180 - x

3. АВСД төртбұрышынан ∠ АВС = x + 50.

Демек,

∠ АВС + ∠ АЕД = x + 50 + 180° - x = 230°

Жауабы: 230°

2 есеп. Шешуі:

Берілген теңдікті түрлендіріп жазсақ, р - ға қатысты квадрат теңдеу аламыз

$p^{2}$ $p^{2}$ + ( n + 1) p - $\ ({n + 1) }^{3}$ $\ ({n + 1) }^{3}$ = 0

Д = $\frac{(n + 1) ^{2}}{4}$ $\frac{(n + 1) ^{2}}{4}$ + $({n + 1) }^{3}$ $({n + 1) }^{3}$ ≥ 0 ⇒ n ≥ -1

$P_{1, 2}$ $P_{1, 2}$ = $\frac{- \ (n\ + 1) \ \pm \sqrt{({n + 1) }^{2} + \ 4({n + 1) }^{3}}}{2}$ $\frac{- \ (n\ + 1) \ \pm \sqrt{({n + 1) }^{2} + \ 4({n + 1) }^{3}}}{2}$

Осыдан, Р бүтін сан болғандықтан, ол жұп сан болады

n = -1 ⇒ $P_{1}$ $P_{1}$ = $P_{2}$ $P_{2}$ = 0

n = 0 ⇒ ${\ P}_{1}$ ${\ P}_{1}$ = $\frac{\sqrt{5} - \ 1}{\ 2}$ $\frac{\sqrt{5} - \ 1}{\ 2}$ , ${\ P}_{2}$ ${\ P}_{2}$ = $- \frac{\sqrt{5} + \ 1}{\ 2}$ $- \frac{\sqrt{5} + \ 1}{\ 2}$

n = 1 ⇒ ${\ P}_{1}$ ${\ P}_{1}$ = 2, ${\ P}_{2}$ ${\ P}_{2}$ = - 4 .

Жауабы: 2

3 есеп. Шешуі:

Теңсіздіктің екі жағын квадраттап алатынымыз

$\sqrt{99 + \ \sqrt{98 + \bullet \bullet \bullet + \sqrt{2 + \sqrt{1$ $\sqrt{99 + \ \sqrt{98 + \bullet \bullet \bullet + \sqrt{2 + \sqrt{1$ < 21. Алынған теңсіздіктің екі жағын тағы да квадраттап табатынымыз:

$\sqrt{98 + \bullet \bullet \bullet + \sqrt{2 + \sqrt{1}}}$ $\sqrt{98 + \bullet \bullet \bullet + \sqrt{2 + \sqrt{1}}}$ < 342. Пайда болған теңсіздіктердің сол жақтары кеми береді, ал оң жақтары керісінше артады. Осылайша 99 рет квадраттағанда теңсіздіктің оң жағында шығатын санды қандай да бір а > 0 саны делік. Ақырында, теңсіздіктің сол жағы 0 - ге тең болады, яғни 0 < а - 3,

ал а -3 >0 ⇒ а>3 .

Сонымен,

$\sqrt{100 + \sqrt{99 + \sqrt{98 + \ldots + \sqrt{2 + \sqrt{1$ $\sqrt{100 + \sqrt{99 + \sqrt{98 + \ldots + \sqrt{2 + \sqrt{1$ < 11

2. тур

4. есептің шешуі:

Есептің шешуін үш жиынның бір - бірімен байланыста қатысты қарастырайық. Бірінші, екінші және үшінші есепті шығарған оқушылар жиыны сәйкесінше А, В және С болсын.

а) жағдай. А жиынының В және С ішкі жиындарын қарастырайық.

Егер С ⊂ В, В ⊂ А онда С⊂А, яғни үш есепті шығарған оқушылар жиыны - ол С жиыны болады. Демек, x - тің ең үлкен мәні 85% ( 1 сурет )

а) жағдайында есеп шығармаған оқушылардың пайызы қарастырылған жоқ. Ендеше

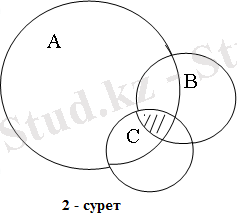
ә) жағдай. А, В және С жиындарының қиылысуын қарастырайық.

$$ Бірінші есепті оқушылардың 2%, екінші есепті 10%,

ал үшінші есепті 15% шығарған жоқ. ( 2 - сурет ) . Үш есепті шығармаған оқушылардың жалпы пайызы:

2% + 10% + 15% = 27%. Жиындардың қиылысуы

3 есепті шығарған оқушылардың пайызын білдіреді. Сонымен, x - тің ең кіші мәні 100% - 27% = 73%

Жауабы: 85% және 73%

5- есептің шешу:

Тік төртбұрыш кестенің өлшемі

m X n делік, яғни келесі кесте берілсін.

$а_{11}$ $а_{11}$ $а_{12}$ $а_{12}$ ∙∙∙ $а_{1n}$ $а_{1n}$

$а_{21}$ $а_{21}$ $а_{22}$ $а_{22}$ ∙∙∙ $а_{2n}$ $а_{2n}$

. . .

$а_{m1}$ $а_{m1}$ $а_{m2}$ $а_{m2}$ ∙∙∙ $а_{mn}$ $а_{mn}$

m ≠ n Әрбір жолдағы ең үлкен және әрбір бағандағы ең іші сандарды жазайық.

$а_{1n}$ $а_{1n}$ ${\ \ \ \ \ а}_{2n}$ ${\ \ \ \ \ а}_{2n}$ ∙∙∙ $а_{mn}$ $а_{mn}$ ең үлкен сандар

$а_{m1}$ $а_{m1}$ ${\ \ \ \ \ а}_{m2}$ ${\ \ \ \ \ а}_{m2}$ ∙∙∙ $а_{mn}$ $а_{mn}$ ең кіші сандар

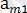
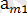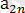
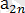
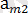
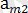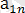
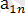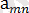
Есептің шартынан 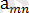${\ \ \ \ \ \ \ а}_{1n}$ ${\ \ \ \ \ \ \ а}_{1n}$ , ∙∙∙ > т. с. с.

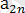
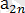
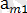
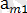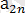
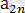
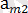
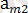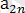
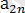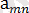
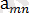, ∙∙∙ > екендігі туындайды.

Айталық, < < ∙∙∙ <

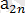
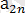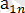
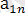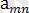
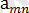
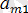
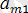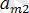
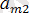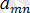
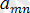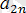
Ал, > >∙∙∙ > болсын. Онда, А = 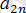және В =

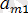
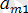
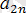
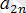
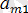
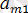болғандықтан, А > В.

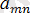
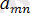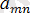
А = , В = 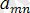жағдайында А = В.

Демек, А ≥ В

Жауабы: А ≥ В

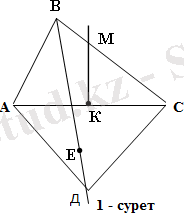
6 есеп. Дәлелдеуі:

1) . К нүктесі АС қабырғасының ортасы

және МК ⊥ АС болсын. ( 1 - сурет )

МК ∩ ВS = Е нүктесі делік (1а - сурет)

2) ВS - биссектриса

АК = СК болғандықтан, АЕ = СЕ, АЕ =R және Е нүктесі шеңбердің центрі болсын.

R = АЕ шеңберіміз МК және ВS түзулерімен N және Д нүктелерінде қиылысады. АN = С N

3) . С N биссектрисасы десек, есеп шартына қарама - қайшылық тудырамыз. Олай болса, СД биссектриса,

ал АЕ = СЕ = ДЕ = R. Сонымен, Е - АСД үшбұрышына сырттай сызылған шеңбердің центрі болып табылады.

11 сынып

1-тур

1. f(x) =cos⁡2x+sin⁡xf(x) = \cos^{2}x + \sin xf(x) =cos⁡2x+sin⁡xf(x) = \cos^{2}x + \sin xфункциясының мәндер облысын табыңыз.
2. -BCBCBCBCқабырғасының ортасы. BE∥AMBE \parallel AMBE∥AMBE \parallel AMжәнеBE=12AMBE = \frac{1}{2}AMBE=12AMBE = \frac{1}{2}AMболатындай, салынған. қақ ортасынан бөлетінін дәлелдеңіз.
3. - натурал сан болсын. 22n+22n−1+12^{2^{n}} + 2^{2^{n - 1}} + 122n+22n−1+12^{2^{n}} + 2^{2^{n - 1}} + 1санының кем дегендеәр түрлі жай бөлгіші болатынын дәлелдеңіз.

2 тур

4. Қабырғаларының ұзындықтары натурал сан және периметрі 40 болатын, әр түрлі доғалбұрышты үшбұрыштардың санын табыңыз.
5. 2x2+2x+3+2x2+2=3x2+2x−1+x2+6\sqrt{2x^{2} + 2x + 3} + \sqrt{2x^{2} + 2} = \sqrt{3x^{2} + 2x - 1} + \sqrt{x^{2} + 6}2x2+2x+3+2x2+2=3x2+2x−1+x2+6\sqrt{2x^{2} + 2x + 3} + \sqrt{2x^{2} + 2} = \sqrt{3x^{2} + 2x - 1} + \sqrt{x^{2} + 6}теңдеуін нақты сандар жиынында шешіңіз.
6. 8×88 \times 88×88 \times 8шахмат тақтасында барлық қара шаршы таңдалып алынатындай және әрбір жолмен әрбір бағанада дәл 7 шаршы таңдалып алынатындай 56 әр түрлі шаршыны қанша тәсілмен таңдап алуға болады?

11 сынып

І тур

1. - есептің шешуі:

1) f (x) = cos ² x + sinx = 1 - sin ² x + sinx

-1≤ sinx ≤1, 0≤ sin ² x ≤1. sinx = -1⇒ y = -1. sinx = 1⇒ y = 1

2) y = cos ² x + sinx = $\frac{1}{2}$ $\frac{1}{2}$ cos2x + 1) + sinx

T ₁ = $\frac{2\pi}{2}$ $\frac{2\pi}{2}$ = π, T ₂ = 2π ⇒ T = 2π

Сондықтан, x ∈ $\left\lbrack - \frac{\pi}{2}; \ \frac{3\pi}{2} \right\rbrack$ $\left\lbrack - \frac{\pi}{2}; \ \frac{3\pi}{2} \right\rbrack$ аралығын қарастырсақ жеткілікті.

3) E (f) = $\lbrack a; b\rbrack$ $\lbrack a; b\rbrack$ болсын, a<0, b> 0

Сонда, sin ² x - sinx + b -1 = 0 және

sin ² x - sinx - a -1 = 0, яғни sinx - ке қатысты екі квадрат теңдеу аламыз.

Д ≥ 0 болғандықтан, b ≤ $\frac{5}{4}$ $\frac{5}{4}$ = 1, 25 және a ≥ - 1, 25

a = -1, 25 ⇒ sin ² x - sinx ≠ 2, 25. b = 1, 25 ⇒ sin ² x - sinx = - 0, 25

Сонымен, a = -1, b = 1, 25

4. f/(x) = cosx (1 - 2sinx) = 0⇒ cosx = 0, sinx =12\frac{1}{2}12\frac{1}{2}⇒ x = -π2\frac{\pi}{2}π2\frac{\pi}{2}және x =π6\frac{\pi}{6}π6\frac{\pi}{6}функцияның кризистік нүктелері болып табылады. Функция[−π2; π6] \left\lbrack - \frac{\pi}{2}; \ \frac{\pi}{6} \right\rbrack[−π2; π6] \left\lbrack - \frac{\pi}{2}; \ \frac{\pi}{6} \right\rbrackаралығында өседі, ал[π6; 3π2] \left\lbrack \frac{\pi}{6}; \ \frac{3\pi}{2} \right\rbrack[π6; 3π2] \left\lbrack \frac{\pi}{6}; \ \frac{3\pi}{2} \right\rbrackаралығында кемиді.

Сонымен, E (f) = $\lbrack - 1; 1, 25\rbrack$ $\lbrack - 1; 1, 25\rbrack$

Жауабы: E (f) = $\lbrack - 1; 1, 25\rbrack$ $\lbrack - 1; 1, 25\rbrack$

2 есеп. Дәлелдеуі:

1) К ∈ АМ АК = МК ( 1 - сурет)

ВЕ ∥ АМ және ВЕ = $\frac{1}{2}$ $\frac{1}{2}$ АМ болғандықтан, ВЕМК параллелограмм, яғни ВК ∥ ЕМ.

АМ⋂ЕД =S ( 1а - сурет)

2. S нүктесі арқылы ЕМ түзуіне параллель түзу жүргізіп, бұл түзудің ВЕ және АД түзулерімен

қиылысу нүктелерін сәйкесінше L және N

деп белгілейік. ЕМ∩АД = 0, ВК∩АД = F

3. ELCM, BESM және MSДC параллелограмм. ВМ = СМ⇒ЕS = ДS

Сонымен, АК = MK = SM, EM ∥ LS ⇒ BK ∥ LS

4. BK ∥ EM ∥ LS Фалес теоремасы бойынша AF = OF = NO және ДN = ON. Осыдан, ДМ = AF = OF яғни АО = ДO. Олай болса, ЕМ түзуі АД кесіндісін қақ ортасынан бөледі.

3 есеп. Дәлелдеуі:

${2^{2}}^{n}$ ${2^{2}}^{n}$ + ${2^{2}}^{n - 1}$ ${2^{2}}^{n - 1}$ +1 = $\left( {2^{2}}^{n - 1} - \ {2^{2}}^{n - 2} + 1 \right) \ \bullet \left( {2^{2}}^{n - 1} + \ {2^{2}}^{n - 2} + 1 \right)$ $\left( {2^{2}}^{n - 1} - \ {2^{2}}^{n - 2} + 1 \right) \ \bullet \left( {2^{2}}^{n - 1} + \ {2^{2}}^{n - 2} + 1 \right)$ =

= $\left( {2^{2}}^{n - 1} - \ {2^{2}}^{n - 2} + 1 \right) \ \bullet \left( {2^{2}}^{n - 2} - \ {2^{2}}^{n - 3} + 1 \right)$ $\left( {2^{2}}^{n - 1} - \ {2^{2}}^{n - 2} + 1 \right) \ \bullet \left( {2^{2}}^{n - 2} - \ {2^{2}}^{n - 3} + 1 \right)$ $\bullet \left( {2^{2}}^{n - 2} + \ {2^{2}}^{n - 3} + 1 \right)$ $\bullet \left( {2^{2}}^{n - 2} + \ {2^{2}}^{n - 3} + 1 \right)$ =

= $\left( {2^{2}}^{n - 1} - \ {2^{2}}^{n - 2} + 1 \right) \ \bullet \left( {2^{2}}^{n - 2} - \ {2^{2}}^{n - 3} + 1 \right)$ $\left( {2^{2}}^{n - 1} - \ {2^{2}}^{n - 2} + 1 \right) \ \bullet \left( {2^{2}}^{n - 2} - \ {2^{2}}^{n - 3} + 1 \right)$ $\bullet \ldots \bullet \left( {2^{2}}^{n - R} + \ {2^{2}}^{n - R - 1} + 1 \right)$ $\bullet \ldots \bullet \left( {2^{2}}^{n - R} + \ {2^{2}}^{n - R - 1} + 1 \right)$

Сонымен,

${2^{2}}^{n}$ ${2^{2}}^{n}$ + ${2^{2}}^{n - 1}$ ${2^{2}}^{n - 1}$ +1 = $\left( {2^{2}}^{n - 1} - \ {2^{2}}^{n - 2} + 1 \right) \ \bullet \left( {2^{2}}^{n - 2} - \ {2^{2}}^{n - 3} + 1 \right)$ $\left( {2^{2}}^{n - 1} - \ {2^{2}}^{n - 2} + 1 \right) \ \bullet \left( {2^{2}}^{n - 2} - \ {2^{2}}^{n - 3} + 1 \right)$ $\bullet \ldots \bullet \left( {2^{2}}^{n - R} + + \ {2^{2}}^{n - R - 1} + 1\ \right)$ $\bullet \ldots \bullet \left( {2^{2}}^{n - R} + + \ {2^{2}}^{n - R - 1} + 1\ \right)$ n ≥ R + 1, R ∈ Z ₀ мысалы, n = 3

${2^{2}}^{3}$ ${2^{2}}^{3}$ + ${2^{2}}^{3 - 1}$ ${2^{2}}^{3 - 1}$ +1= $\left( {2^{2}}^{3 - 1} - \ {2^{2}}^{3 - 2} + 1 \right) \left( {2^{2}}^{3 - 2} - \ {2^{2}}^{3 - 3} + 1 \right) \left( {2^{2}}^{3 - 2} + \ {2^{2}}^{3 - 3} + 1 \right)$ $\left( {2^{2}}^{3 - 1} - \ {2^{2}}^{3 - 2} + 1 \right) \left( {2^{2}}^{3 - 2} - \ {2^{2}}^{3 - 3} + 1 \right) \left( {2^{2}}^{3 - 2} + \ {2^{2}}^{3 - 3} + 1 \right)$ =

=13∙3∙7 Демек, n натурал сан болғанда ${{\ \ 2}^{2}}^{n}$ ${{\ \ 2}^{2}}^{n}$ + ${2^{2}}^{n - 1}$ ${2^{2}}^{n - 1}$ +1 cанының кем дегенде n әртүрлі жай бөлгіші болады. д. к. о. е.

ІІ тур

4 есеп. Шешуі:

Есеп шарты бойынша үшбұрыш қабырғаларының ұзындықтары а, в және с натурал сандар

а + в + с = 40 ⇒ с = 40 - (а + в )

1. {а+в>40−(а+в) а−в<40−(а+в) \left\{ \begin{array}{r} а + в\ > 40 - (а + в) \\ а - в\ < 40 - (а + в) \end{array} \right. \{а+в>40−(а+в) а−в<40−(а+в) \left\{ \begin{array}{r} а + в\ > 40 - (а + в) \\ а - в\ < 40 - (а + в) \end{array} \right. \⇒(а+в>20а, в, с<20) \ \binom{а + в\ > 20}{\ \ а, в, с < 20}\(а+в>20а, в, с<20) \ \binom{а + в\ > 20}{\ \ а, в, с < 20}\⇒ 1≤ а ≤ 19

Егер а = 1 болса, онда в>19 ал в≠20

a = 2 ⇒ в>18, яғни в = 19 және с = 19.

Сонымен, 2 ≤ а ≤ 19, 2 ≤ в ≤ 19 және 2 ≤ с ≤ 19, .

a = 3 ⇒ в>17, ендеше, в = 18 және с = 19. Осылайша егер а - ның кезекті мәні а =10 болса, онда в = 11, с = 19

ал а =11 болғанда, онда в = 10, с = 19, яғни соңғы екі үшбұрыш бір - біріне тең болады. Ендеше, 2 ≤ а ≤ 13

2) Осы алынған теңсіздіктерге байланысты периметрі 40 болатын үшбұрыштар кестесін құрайық:

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс