Функцияның кризистік нүктелері

Экономика саласын таңдаған оқушылар үшін математика пәнінен эллективті курс бағдарламасы

Габитова Зарина Маратқызы

СҚО, Уәлиханов ауданы, Көктерек ауылы,

Елтай орта мектебі

математика пәнінің мұғалімі

ТҮСІНІК ХАТ

Мектепте оқитын оқушыларды математикаға деген көзқарас бойынша бірнеше топтарға бөлуге болады: математиканы тек мектепте оқып, әрі қарай өмірде қолданбайтын оқушылар тобы; болашақта математикамен байланысты мамандықты таңдап алатын оқушылар тобы.

Бұл бағдарлама математиканы өмірде қолданатын, әрі басқа мамандықтарға қажет ететін жаратылыстану-математика бағытында оқитын 10 сыныптар үшін ұсынылып отыр. Экономика саласын таңдаған оқушыларға қаржы заңдарын білу қажет. Қаржы заңдарын дұрыс меңгермеген, әрі есептеуді баяу жүргізетін оқушы болашақта жақсы маман иесі болатындығына күмән келтіріледі.

Ұсынылып отырған бағдарламада жас ұрпақтың қоғамдық өміріндегі экономикалық тәрбиенің мәні мен маңызын ашып көрсетіп, математикадан сыныптан тыс жұмыстарда экономикалық тәрбие берудің нақтылы жолдарын анықтау мәселелері қарастырылады.

Қолданбалы курсы оқушыға экономикалық есепті математика тіліне аударған қандай да бір гипотезаны дәлелдеуге мүмкіндік береді. Сонымен қатар ұсынылып отырған курс:

• оқушылардың математикалық білімнің өмірдегі қолданылуымен таныстыру арқылы математикалық білім сапасын арттыруға;
• оқушылардың өмірдінде кездесетін экономикалық міндеттерін шешуде;
• оқушылардың ойлау қабілеттерін дамытуға, өз бетінше тұжырымдай алуға жағдай жасау, мүмкінділік жасаумен сипатталады.

Берілген курс 10 сыныпқа 34 сағатқа (аптасына 1 рет) есептелген.

Мақсаты: математикадан алған теориялық білімдерінің экономикадағы қолданылуымен оқушыларды таныстыру. Оқушылардың есептеу мәдениетін қалыптастыру.

Міндеттері:

• математиканың білім қолданылымы айқын көрінетін экономикалық тақырыптармен таныстыру;
• экономикалық есептердің түрлерімен таныстыру;
• қоршаған орта туралы көзқарастарын математикалық тұрғыдан дамыту;
• математикалық білімдерін экономикалық есептеуде қолдана алу;
• экономикалық мәтінді есептер бойынша оқушыларға білімді меңгертудегі математиканың рөлін көрсету;
• белгілі бір іс-әрекетті жүзеге асыру арқылы оқушылардың ойлауын толық тұжырымдай алуға тәрбиелеу;
• экономика, өндірісті дамыту үшін ғылым прогресіне қажеттілік туралы түсініктерін қалыптастыру;
• экономикамен байланысты мамандыққа бағдар беру.

Курсқа қойылатын талаптар

қолданбалы курс лекция және семинар сабақтары түрінде өткізіледі. Әсіресе, экономикалық мағынасы бар практикалық есептерге мән беріледі.

• Зерттеу жұмыстары, баяндамалар беріледі. Оқу курсының бақылауы сынақ сабақтар, тест және конференциялар түрінде жүргізіледі.

Оқушылардан күтілетін нәтиже

қолданбалы курсын оқу кезінде оқушылар:

• микрокалькуляторды пайдаланып есептей алу;
• процент, берілген санның процентін таба білу;
• экономикалық мәселелерді шешетін математикалық білімді қолдана алу;
• математикалық модельдердің негізгі принциптерін қолдана алу;
• өмір жағдайларында математикалық әдістерді қолдана алу;
• өздігінен зерттеу жұмысын ұйымдастыра алу;
• практикалық есептерді шығармашыл есептей алу қажет.

Бағдарламаның мазмұндық бөлігі

Кіріспе

Жалпы түсінік. Мақсаты.

Микрокалькулятор

Микрокалькулятор. Микрокалькулятордың қолданылуы.

Пайыз. Пропорция

Пайыз. Берілген санның поцентін табу. Пайыздарға берілген есептер.

Пропорцияның белгісіз мүшесін табу.

Қарапайым экономикалық сөз есептер

Экономикалық сөз есептер.

Функция.

Функция. Функциялардың экономикадағы қолданулары.

Туынды

Туындының экономикалық мағынасы. Туындының экономикада қолдану. Функцияның икемділік қасиеттері.

Интеграл

Интеграл. Интеграл түрлері. Анықталған интегралдың экономикалық мағынасы Анықталған интеграл ұғымын экономикада қолдану.

Дифференциалдық теңдеулер

Бір айнымалы функцияның икемділік ұғымы. Экономикалық зерттеулерде кездесетін кейбір екі айнымалы функциялар.

Зерттеу жұмысы

Практикалық сабақ. Жоба қорғау

Қорытынды сабақ

Қолданылатын әдебиеттер тізімі:

1. «Алгебра және анализ бастамалары», оқу құралы, 10-11 сыныптары
2. Түнғатаров Ә., «Экономикалық мамандықтарға арналған жоғары математика курсы»
3. «Экономикалық-математикалық модельдеу»
4. Айдос Е. «Жоғары математика»
5. Асқарова Ж. «Экономикадағы математикалық әдістер»
6. Есептеулер жинақтары

Күнтізбелік - тақырыптық жоспарлау

1-сабақ. Кіріспе

Ғылымдар ішінде математика ерекше орын алады. Математика-нақты өмірдің сандық қатыстары мен кеңістіктегі түрлері туралы ғылым.

Математика басқа ғылымдарға табиғат құбылыстары арасындағы түрлі қатыстарды өрнектеу үшін, сандар мен символдар тілін ұсынады. Бірақ математиканы қолданбас бұрын биолог, физик немесе экономист зерттелетін құбылыс мәнін терең түсінуі қажет, оны математикалық түрде өңдеуге болатындай етіп бөліктеуі керек.

Математикадағы зерттеу обьектілері - қоғам мен, табиғат құбылыстарын сипаттау үшін құрылған логикалық модельдер. Математика осы модельдер элементтеррінің арасындағы қатыстарды зерттейді.

Бір ғана математикалқы модель өзінің абстракциялылығын әртүрлі процестерді сипаттай алады. Мысалы, бір дифференциалдық теңдеу радтоактивті ыдырауы да, дене температурасының өзгерісін сипаттайды.

Экономикалық есептердің қайсысын да алмасаң, математикалық модельдерсіз шығару мүмкін емес.

2 сабақ. Микрокалькулятор. Микрокалькулятормен есептеу

Математикада, экономикада болмасын, есептеуді шапшаң орындау үшін электрондық есептеу машиналары пайдалынады. Олардың ішіндегі қарапайымы - микрокалькулятор.

Кез келген микрокалькулятордың бет панелінде клавиатура және экран орналасқан. Клавиатурасында 0-ден 9-ға дейінгі цифрлар, арифметикалық төрт амал таңбасы, теңдік таңбас, т. б бар.

Қазіргі жаңа заманда микрокалькулятордың сан алуан түрлері бар. Олар арифметикалық амалдардың түрлісін орындайды.

Микрокалькуляторлар бүтін сандармен және ондықбөлшектермен амалдар рындайды. Микрокалькуляторға бүтін сандарды және ондық бөлшектерді ендіру олардың жазылуына сәйкес орындалады. Егер микрокалькуляторға теріс сан ендірукерек болса, онда көптеген микрокалькуляторда «-» таңбалы клавишаны пайдаланады, бұл экономикада кеңінен қолданылады.

Микрокалькуляторда екі санға арифметикалық бір амал рындау үшін оған бірінші санды ендіріп, тиісті амалдың таңбасы бар клавишаны басу керек, содан соң екінші санды ендіріп, теңдік таңбасы бар клавишаны басу керек. Нәтижесі экранда көрінеді.

Есептер шығару

1. Микрокалькуляторға мына сандарды ендіріп, жай 0, 1 дәлдікпен есепте:; ; 14, 265 : 478, 2
2. Жанар жылына 384658 теңге жалақы алады. Ай сайын 0, 1% табыс салығын төлейді. Есептеу керек:

а) Жанар жылына неше теңге табыс салығын төлейді;

б) Жанар ай сайын қолына неше теңге жалақы алады?

Микрокалькулятормен есепте.

3. Микрокалькулятордың көмеген отбасы бюджетін есепте.

3сабақ. Пайыз. Пропорция

Күнделікті өмірде әртүрлі шамалардың жүздік үлестерін жиі кездестіреміз, әрі табыстың үлесін тапқымыз келеді немесе жұмыс көлемін есептегіміз келеді. Мұндай септеулерді жүргізу барысында пайызды қолданған тиімді. Экономикада пайыз көп қолданылады. Бөлшектің жүзден бір бөлігін пайыз (процент) деп атаймыз.

Пайыз (процент) сөзі латын тілінен аударғанда - «жүздік» немесе «жүзден» деген мағынаны береді.

Пайыз Үндістанда V ғасырда белгілі болған, ал Еуропада ХVІ ғасырда қолданыла бастады.

Пайызды Римде кең қолданған. Римдіктер ақшаны пайыз деп атаған. Римдіктер арқылы Еуропа елдері пайызбен танысқан. Көп уақытқа дейін пайызды әрбір 100 бірлікке келетін кіріс пен қарыз деп түсінген.

Пайыз сөзінің орнына % белгісі қолданылады және ол белгі санан кейін қолданылады. Пайызды санмен өрнектеу үшін пайыз белгісін алып тастап, пайыз санын 100-ге бөледі. Санның 1%-ы белгілі болған жағдайда, санды (шаманы) табу үшін 1%-ды беретін санды 100-ге көбейту керек.

Мысал қарастырайық, Жұмысшы айына 23000 теңге табыс алатын. Осы жылдан бастап оның табысы 27600 теңге болды. Жұмысшының табысы неше пайызға өсті?

Шешуі: Жұмысшының табысына неше теңге қосылғанын анықтау керек. Кейін ғана пайызын есептеп аламыз. Жауабында, жұмысшының табысы 20%-ға өсті.

Екі санның бөліндісі сол сандардың қатынасы деп аталады, ал екі қатынастың теңдігі пропорция деп аталады.

Мысал, сүттен алынатын ірімшіктің массасы сүттің массасының 8%-індей. 200 кг сүттен неше кг ірімшік алынады?

Шешуі: 200кг сүттен алынатын ірімшіктің массасы белгісіз (айнымалы), сондытан оны х деп белгілейміз.

200 кг-100%

х кг - 8%

200/ х =100/8; Жауабы, сүттен алынатын ірімшіктің массасы 16 кг.

Есептер шығару

1. 1л бензиннің массасы 690г, ал оның 1л керосинмен қоса алғандағы массасы 1485г. 1л бензиннің масасы 1л керосиннің массасының қанша пайызын құрайды?
2. Банк салымшыларға қысқа мерзімді салым бойынша 3, 5% жылдық сыйақы төлейді (салым жыл сайын 3, 5%-ға өсіп отырады) . Бір жылдан соң салымшы 207000 тг алса, ол банкке алғашқыда қанша теңге салған?
3. Тауар бағасы 100%-ға өсті. Тауар бағасы қанша есе өсті?
4. Жалақы 30%-ға көтерілсе, 1, 3 есе өсті деп айтуға бола ма?
5. Ұялы телефон 21000тг тұрады. Бұл баға 8%-ға төмендеді. Кейін баға тағы 15%-ға төмендеді. Екінші рет төмендетілген соң ұялы телефонның бағасы қандай болды?

4сабақ. Проценттерге берілген есептер. Пропорцияның белгісіз мүшесін табу

1. Калькулятордың бағасын алдымен 25%-ке, ал содан соң тағы да 65%-ке арттырды. Калькулятордың бағасы қанша есе өсті?
2. Калькулятордың бағасын алдымен 25%-ке, ал содан соң тағы 65%-ке арттырды. Калькулятордың бағасы қанша есе өсті?
3. Пропорцияның алғашқы үш мүшесінің қосындысы 58-ге тең. Үшінші мүшесі бірінші мүшесінің-сін, екіншісі-ін құрайды. Пропорцияның төртінші мүшесін табыңыз.
4. 1999 жылғы санақ қорытындысы бойынша елімізде 14953000 адам тұрған. Оның 53, 4%-ын қазақтар, 30%-ын орыстар, 3, 7%-ын украиндер, 2, 5%-ын өзбектер, 2, 4%-ын немістер, 1, 4-ын ұйғырлар, 0, 7%-ын кәрістер және 5, 9%-ын басқа ұлттар құраған. 1 жылғы санақ қорытындысы бойынша елімізде аталған ұлттардан қанша адам тұрған?
5. Айналып тұрған доңғалақтың бұрылу бұрышы уақыт квадратына пропорционал. Доңғалақ бірінші рет 8 секундта бір айналып шықты. Айнала бастағаннан 48 с өткеннен кейін доңғалақтың бұрыштық жылдамдығы қандай еді?
6. 40 г тұзы бар ерітіндіге 200 г су қосысылды да, оның концентрациясы 10% кеміді. Ерітіндіде әуелде қанша су бар еді және концентрациясы қандай еді?
7. Екі кесек жездің массасы 30кг. Бірінші кесекте 5кг, екіншісінде 4 кг таза мыс бар. Егер екінші кесектегі мыс біріншідегіден 15% артық болса, бірінші кесектегі мыс неше пайыз (процент) болады?

5-6 сабақ. Қарапайым сөз есептердегі экономика

1. Жинақ кассасынан ақша сатушы әуелде өз ақшасының 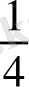бөлігін алып, екінші рет қалған ақшасының 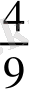бөлігін және 640 теңге алды. Ақшасын екі рет алғаннан кейін жинақ кітапшасында барлық салған ақшасының 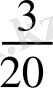бөлігі қалды. Басында салған ақшаның мөлшері қандай еді?

8. Кварталда 8 көпқабатты уй салынды. Олардың орташа биіктігі 38 м. Егер сегіз үйдің төртеуінің орташа биіктігі 29 м болса, онда қалған төрт үйдің орташа биіктігі қандай болғаны?

Бірінші жұмысшы жұмысты 10 күнде бітіреді, ал екінші жұмысшы сол жұмысты 15 күнде бітіре алады. Екеуі бірлесіп, осы жұмысты неше күнде бітіреді

9. Салымшы жинақ кассадан салынған ақшасының алдыменбөлігін, келесі жолы қалған ақшасыныңбөлігін және 640 теңге алды. Содан кейін жинақ кітапшасында барлық ақшасыныңбөлігі қалды. Алғашқыда салған ақшасы қанша теңге еді?
10. Үш жұмысшының жалпы табысы 4080 теңге. Бірінші және екінші жұмысшының табыстарықатынасындай, ал үшінші жұмысшының табысы бірінші жұмысшының табысыныңқұрайды. Әр жұмысшының табысын анықтаңыз.
11. Үш санның екіншісі біріншісінен қанша үлкен болса, үшіншісі екіншісінен сонша үлкен. Егер екі кіші сандардың көбейтіндісі 85-ке тең, ал екі үлкен сандардың көбейтіндісі 115-ке тең болса, сол үш санды табыңыз.
12. Егер берілген саннан оның алтыдан бір бөлігін азайтып, осы айырмаға санның бестен бір бөлігін қоссақ, онда 9, 3 саны шығады. Берілген санды табыңыз.

7-8сабақ. Функция ұғымы. Экономикада функцияның қолданылуы (сызықтық)

D қандай да бір сандар жиыны болсын. Егер әрбір х € D санына толық анықталған жалғыз у санын сәйкес қоятын f ережесі көрсетілсе, онда D жиынында анықталған сандық мәнді функция берілді дейді және оны y=f(x) x€D деп белгілейді. D - функцияның анықталу аймағы, ал Е={y €R: y=f(x) x€D } - функцияның мәндер жиыны деп аталады. Бұл жағдайда Е жиыны D жиынының f функция бойынша алынған бейнесі деп аталады. Функциялар әр түрлі болады. Біз сызықтық функцияны қарастырамыз.

Функцияларды әр түрлі тәсілдермен беруге болады.

1. Кестелік тәсіл . Функция кесте түрінде берілуі мүмкін. Экономикада сұраныс пен ұсыныс тақырыбын өткен кезде функция қолданылып, кесте түрінде беріледі. Сұраныс пен ұсыныстың өзгеруін көрсету үшін ең алдымен кесте толтырылуы қажет.

Мысал. Күніне сүтті 5 литрден сатады. Егер күн сайын сүтке деген сұраныс екі есе артатын болса, күн сайынғы сұранысты көрсетіңдер.

х-күндер, у - сұраныстың өзгеруі; у=2x

2. Графиктік тәсіл. Функцияның графиктері функцияға байланысты. Сұраныс пен ұсыныстың графигін біздің есепте түзу арқылы көрсетуге болады.

у

сұраныстың өзгеруі

0. х

3. Аналитикалық тәсіл. Аналитикалық тәсіл экономикада көп қолданылмайды. Бұл тек қана есептердің шешімін табуда қолданылады.

Есептер шығару

1. Функцияларының анықталу аймағын табу керек:y=arcsin(2x+1) y=сos(х-π/3) y=2+4/х-3f(x) =x+1/xфункциясының -1; ½; 10 нүктелеріндегі; f(x) =x2+2xфункциясының -π/4; 0; 5π/12 нүктелеріндегі мәндерін тап.

3. Функциялардың графиктерін сал:

3. 1 y=1/х-3

3. 2 y=1+2sinx

3. 3 y=2+1/x

9-10сабақ. Экономикада функцияның қолданылуы (бөлшек рационал, дәрежелі, көрсеткіштік, логорифмдік)

Экономикалық теория мен тәжірибеде сызықтық
функциялардан бастап зерттеліп отырған заттың әр түрлі уақыттағы
жағдайларын байланыстыратын рекуренттік катынастар арқылы
анықталатын белгілі алгоритмдермен құрылған функцияларға
дейінгі көптеген функциялар кеңінен пайдаланылады. Онда
сызықтық функциялармен катар бөлшек рационал, дәрежелі
(квадраттық, кубтық және т. б. ), көрсеткіштік, логорифмдік және
басқа да функциялар қолданылады. Бірқатар экономикалық
құбылыстардың периодтылығы, өзгеру зандылығы тригонометриялық функцияларды қолдануға мүмкіндік береді. Экономикада өте жиі қолданылатын кейбір функцияларды келтіріп кетейік.

1. Сұраным, пайдаланым және ұсыным функциялары жеке бұйымдарға немесе ұсыныстарға сұраным, пайдаланым және ұсыным көлемдерінің (мөлшерлерінің) әр түрлі жағдайлардан (мысалы, бағадан, түсімнен, т. б. ) калай тәуелділігін көрсетеді. Мысалы, заттың бағасы. Р тенге болса, онда белгілі бір шарттар орындалғанда сол затқа сұраным q оның бағасына тәуелді. яғни q=f(p) - сұраным функциясы болады. Кей жағдайларда бағаны сұранымға тәуелді етіп талдау жүргізуге, яғни p=f(q) функциясын зертеуге тура келеді.

2. Өндіріс функциясы өндіріс нәтижелерінің оларға жұмсалатын өндіріс күштерінен, себептерден қалай тәуелділігін көрсетеді.

3. Шығын функциясы (өндіріс функциясыныі бір түрі) өндіріс шығындарының өндіріс нәтижелерін (өнімдеріне) қалай тәеулділігін көрсетеді. Мысалы, егер х өндірілетін өнім мөлшері (көлемі) болғанда зат өндірілгенде кететін жалпы шығынды К(х) арқылы белгілесек, онда К(х) /х функциясын орта немесе меншікті шығын функциясы деп атайды. Ол Р(х) арқылы белгіленеді, яғни Р(х) =К(х) /х

4. Түсім функциясы (өндіріс функциясының дербес түрі) өнім көлемінің оны шығаруға жқмсалатын шикі заттардан, жқмыс күшінен қалай тәуелділігін береді. Мысалы, егер q мөлшерде зат сатылса, онда осы сатылған зат көлемінің әр заттың бағасына көбейтсек, жалпы түсім шығады, яғни U=p∙q = q∙f(q) функциясы пайда болады. Бұл функцияны жалпы түсім функциясы деп атайды.

5. Пайдалылық (басымдылық беру) функциялары кең мағынада іс нәтижесінің осы істі жүргізу деңгейіне қалай тәуелділігін көрсетеді.

Есептер шығару

1. Функцияның ең кіші оң периодын тауып, графигін сал:y=sin2xy=cosx/3y=3tg1, 5x
2. Өз сыныбында қандай да бір затты алып, оны достарына ұсын. Сұраныс пен ұсынысты зерттеп, графигін сал.

11сабақ. Шектер және үзіліссіздік. Пайызды үзіліссіз қосу есептері

Егер y=f (x) функциясы:

1. х0нүктесінде анықталған;
2. х0нүктесінің қандай да бір Uõ(х0) маңайында анықталған;
3. limx→0f (x) = f (x0) теңдігі орындалса, онда ол х0нүктесінде үзіліссіз функция деп аталады.

Бұл анықтаманы кванторларды пайдаланып былайша жазуға болады:

f (x) функциясы x ₀ нүктесінде үзіліссіз,

lim _x→x0 f(x) =f ( lim _x→x0 x)

Бұдан, егер функция үзіліссіз болса, онда функция астында шекке өтуге болатынын, басқаша айтқанда, үзіліссіз функция мен шек таңбаларын өзара орын ауыстыруға болатынын көреміз.

Мысалы, lim sinx= lim sinx=sinπ/2=1 (sinx функциясының кез келген х€R нүктесінде үзіліссіз екені төменде көрсетіледі) .

y=f(x) функциясының х ₀ нүктесінде үзіліссіз болуы үшін, оның х ₀ нүктесінің оң жағында да, сол жағында да үзіліссіз болуы қажетті және жеткілікті:

lim _x→x0+ f(x) = f(x ₀ ) = lim _x→x0- f(x)

f(x) функциясының х ₀ нүктесінде үзіліссіз болу анықтамасын

lim _x→x0 [f(x) - f(x) ] =0

lim _{ħ →0} [f(x ₀ + ħ ) - f(x ₀ ) ] = 0

lim _{∆x →0} [f(x ₀ + ∆x ) - f(x ₀ ) ] =0

lim _{∆x →0} ∆у=0

жіне т. с. с. түрлерінде де жазады. Мұнда ∆x=х - x ₀ =һ саны аргументтің x ₀ нүктесінде өсімшесі, ∆у= f(x) - f(x ₀ ) = f(x ₀ +һ) - f(x ₀ ) = f(x ₀ +∆x) - f(x ₀ ) саны функцияның x ₀ нүктесіндегі өсімшесі деп аталады.

Экономикада нарықта болып жатқан өзгеріс жағдайды үзіліссіздік арқылы көруге болады.

Мәселен, нарықта айдың алғашқы мен соңында болған өзгерісі көрсетілген (текті үзілісті функция арқылы)

Б А - айдың басы

С С - соңында

0

Есептер шығару

1. Көрсетілгендердің шектерін тап:limх→-25х2+13х+6/3х2+2х-8limх→43х2-10х-8/4х2+6х-64

1. 3lim _х→∞ 7х ⁴ +2х ³ +5/6х ⁴ +3х ² -7х

2. Берілген функциялардың үзіліссіздігін зертте, графигін сал:

x+4, х<-1

2. 1 f(x) = х ² +2, -1≤х<1

2х, х≥1

sinx, х<0

2. 2 f(x) = х, 0≤х≤2

0, х>2

3. f(x) =cos2x-cos32xжәнеφ(x) =3x2-5x3функцияларых→0ұмтылғанда, реттері бірдей ақырсыз кішкене болатынын дәлелдеу керек.

Функцияның кризистік нүктелері мен экстремум нүктелері

Туынды және оның қолданылуы

Кері тригонометриялық функциялар

Теңдеуге есептер шешу

Функцияның экстремумдері

Сағат саны

Функцияның қасиеттері. Экстремумдары

Функцияның ең үлкен және ең кіші мәндері

Функция графигін салу

Функцияны зерттеу және оның графигін салу туралы

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс