Шектер туралы теоремалар

Тақырыбы:_Шектер туралы теоремалар
Сабақтың мақсаты
Білімділік: Тақырыпты түсіндіріп,есептер шығара білуге үйрету.
Дамытушылық: Өзбетімен жұмыс істеуге,шығармашылықпен ізденуге дағдыландыру.
Тәрбиелік: Ұқыптылыққа байқампаздыққа, жауапкершілікке тәрбиелеу.
Сабақтың типі: аралас сабақ.
Сабақтың қамтамасыздандылуы:
а)оқу көрнекілік
құралдар: электронды оқулық материалдарды, слаидтар,анықтамалық кестелер.
б)үлестірмелі
материалдар: жекелеме карточкалар.
в)ТОҚ: компьютер, проэктор,экран.
Пәнаралық
байланыс: физика, информатика
Қолданатын әдебиет:
Негізгі: 1)10-11 сынып алгебра авторы А.Е.Абылқасымова
2)курс высшей математики для сред. спецалистов автор Н.П.Гарасов.
Қосымша: тест материалдары.қосымша деректер,
Өз бетінше
жұмыс: деңгейлік тапсырмалар. А,В,С нұсқалары бойынша.
Сабақтың өту барысы:
Ұйымдастыру
кезеңі: 1) Оқушыларды түгендеу,жинақтау.
Оқушылардың біліктілігі мен дағдысын тексеру
1) Өткен тақырыптарды пысықтау.

а) сұрақ-жауап әдісі

ә) жекелеме деңгейлік тапсырмалар.

б) үйге берілген есептерді талдау.

Егер 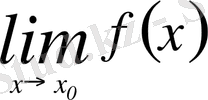- шегі бар болса (кейде оны 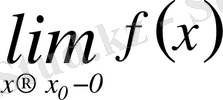немесе
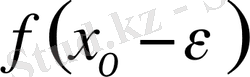интерактивті тақта, карточка
деп те белгілейді), онда оны функция 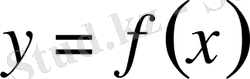-тің х х0-ге сол жағынан
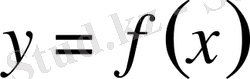ұмтылғандағы шегі деп атайды. Дәл осы сияқты функция -тің х х0-ге оң
жағынан ұмтылғандағы шегі 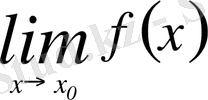анықтауға болады.
Функцияның оң жақты және сол жақты шектерін оның бір жақты шектері
деп атайды.
Функция 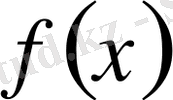-тің х0-дегі шегі болуы үшін оның оң жақты және сол
жақты шектерінің болуы қажетті және жеткілікті, яғни .
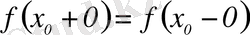Функция шектері жөнінде келесі теоремалар орынды болады:
Теорема. Айталық, 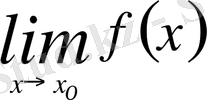және 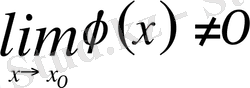бар болсын, онда 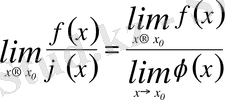болады (мұнда
болуы да мүмкін).
Егер осы теоремалардың шарттары орындалмаса, онда 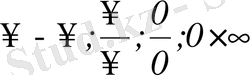түріндегі
анықталмағандықтар жүз беруі мүмкін, ондай анықталмағандықтар алгебралық
түрлендірулер арқылы айқындалады.
1-мысал. 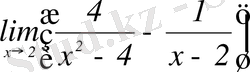- шегін табыңыз.
Шешуі: Біз мұнда -анықталмағандығына душар боламыз. Оны айқындау үшін
жақша ішіндегі өрнекті ортақ бөлімге келтіреміз. Сонда 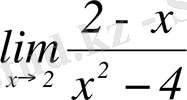-ті аламыз, бұл
бізге 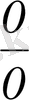-анықталмағандығын береді, сондықтан х-тің орнына 2-ні қоймай
тұрып, яғни, шек астындағы өрнекті (х-2)-ге қысқартамыз. Сонда 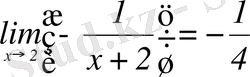-ді
аламыз.
2-мысал. 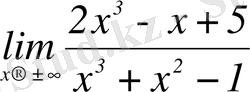-шегін табыңыз.
Шешуі: Мұнда 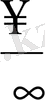-анықталмағандығын аламыз. Оны айқындау үшін шек
астындағы бөлшектің алымын да, бөлімін де х3-ке бөлеміз. Сонда:
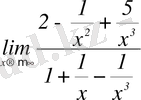шек астындағы бөлшектің бөлімінің шегі 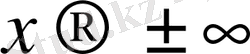ұмтылғанда нөлден
өзгеше, олай болса оған 2-теореманы қолдануға болады, яғни,

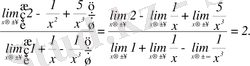
№3

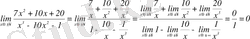
№4

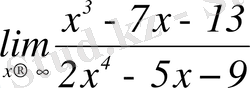
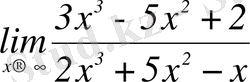Сабақтың қорытындысы:
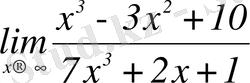қолы:
-----------------------
№2 карточка
1.
2.

№1 карточка
1.
2.

№4 карточка
1.
2.

№3 карточка
1.
2.

№6 карточка
1.
2.

№5 карточка
1.
2.