Айналу денесі. Конус: анықтама, қималар және бетінің ауданы - сабақ жоспары


ӘБ отырысында Бекітемін
қаралды Әдіскер
«»2015ж. «»2015ж.
Қарқымбаева Г. Б. Альчембаева У. С.
Тақырыбы:
Математика пәні мұғалімі: Қарқымбаева Г. Б.
2014-2015 оқу жылы
Күні: 23. 02. 2015ж.
Тобы: ПУ-13
Пәні: математика
Сабақтың тақырыбы: Айналу денесі. Конус
Сабақтың мақсаты:
Білімділік: Айналу денесі цилиндрді қайталай отырып, оқушыларға ерекше геометриялық фигура конусты, конус элементтерін, конус жазбасын таныстыру, конустың бүйір бетінің ауданын табу формуласын қорытып, есептер шығаруда қолдануға үйрету.
Дамытушылық: Оқушының өз бетімен оқып-үйренуі үшін ең алдымен танымдық белсенділігін арттыру, ойлау белсенділігін арттыру, білімге сай дағдыларын қалыптастыру арқылы іскерлігін дамыту.
Тәрбиелік: Белсенділігі жоғары, теориялық білімін есеп шығаруда қолдана білетін білімді тұлға тәрбиелеу.
Сабақтың түрі: Жаңа білімді меңгерту
Өту әдісі: сын тұрғысынан ойлау
Көрнекіліктер: интербелсенді тақта
Пән аралық байланыс: технология, әдебиет, сызу
Сабақтың барысы
Ұйымдастыру кезеңі
а) Амандасу. Оқушының зейінін сабаққа аудару.
ә) Үй есебін тексеру
І. Ой қозғау. «Не білемін?»
Бұл кезеңде оқушылардың өткен айналу денесі, оның ішінде цилиндр туралы біліміне бақылау жасау
- Айналу денегісі дегеніміз не?
/Қандайда бір шектелген, жазық облыс өзінің шекарасымен бірге осы жазықтықта жатқан осьтен айналғанда пайда болған жазық емес фигура айналу денесі деп аталады. /
- Жақсы олай болса айналу денесіне өмірде қандай мысалдар келтіруге болады?
/Құдықтан су алуға барғанда шелектің бауын осьтен айналдыра цилиндр тәріздес орамаға ораймыз/
/самалюттің ебелектері, станоктардың айналу тетіктері/, /айналу өсі бар дене шахмат фигуралары, вазаның да айналу өсі бар/
- Олай болса біз айналу денелерінің ішінде цилиндрді қарастырдық, кім цилиндрге анықтама береді?
/Цилиндр деп тіктөртбұрышты оның қабырғаларының бірінен айналдырғанда шығатын денені айтамыз/
- Цилиндр сөзі қай елдің сөзінен шыққан және қандай мағананы береді?
/гректің «kulindros» сөзінен шыққан, ол «валик», бізше «оқтау» деген мағананы береді/
- Жақсы олай болса цилиндрдің элементтеріне және қималарына тоқталайық.
- цилиндрдің жасаушысы, осі, қимасы, осьтік қимасы, дөңгелек қима, эллипс тәріздес қимасын қалай аламыз? (сурет бойынша)
- Цилиндрдің бүйір бетінің ауданы / Sб. б=2πRH
- Толық бетінің ауданы /Sтол. б. =2 πRH+2 πR2/
- Қазақтың ұлттық киімінде цилиндр тіріздес түрі кездесе ме?
/ қыз баланың тақиясы (суретін көрсету) /
ІІ. Мағынаны ажырату. «Не білгім келеді?»
Жаңа сабақ.
- Бүгін біз тағы бір ерекше геометриялық дене конуспен танысымыз. Слайд арқылы.
Өздерің көріп отырғандай тік бұрышты үшбұрышты оның бір катеті арқылы өтетін l өсімен айналдырсақ, нәтижесінде, айналу денесі - конусты аламыз. Яғыни, конус дегеніміз тікбұрышты үшбұрышты бір катетінен айналдырғанда шығатын денені айтады екенбіз. (Слайдпен көрсету)
- АО катеті айналғанда конустың табаны болатын дөңгелек шығады.
- Конустың табан жазықтығы оның ҒО өсіне перпендикуляр. ˂ ҒОА= 900
- Конустың төбесінен оның табан жазықтығына жүргізілген перпендикуляр конустың биіктігі болып табылады.
- ҒА гипотенузасын өстен айналдырғанда конустың бүйір бетін сызып шығады.
- Табан шеңберінің кез келген нүктесін конустың Ғ төбесімен қосатын кесінділер конустың жасаушылары болып табылады және олар бір-біріне тең. Олар конустың бүйір бетін құрайды.
- Табаны дөңгелек және биіктігінің табаны дөңгелектің центріне дәл түсетін конусты тік дөңгелек конус деп атаймыз. Конус грекше «konos»- «қарағай бүршігі» дегенді білдіреді
- Мына конусқа назар аударайық. Бұл тік емес конус. Мұндай конустар мектеп курысында қарастырылмайды. Бұл конус айналу денесі болмайды. (46 сурет)
- Конустың жазықтықпен қимасы.
Конуспен жазықтықтың қиылысуы конустың бөлігі болуы мүмкін. Бұл жағыдайда біз әртүрлі қималар аламыз.
- Конустың екі жасаушысын қамтитын екі түзу арқылы α жазықтығжүргізуге болады. Бұл жазықтық конустың табанын хорда бойымен, ал бүйір бетін екі жасаушысы бойымен қиып өтеді. Сонда шыққан қима қандай үшбұрыш болды? (теңбүйірлі) (1 сурет)
- Егер α жазықтық конустың өсі арқылы өтсе, онда пайда болған қима өстік қима болады. (2сурет)
- Конусты оның өсіне перпендикуляр α жазықтықпен қиюға болады, қиюшы жазықтық табан жазықтығына параллел болса, қима дөңгелек болады.
- Егер конустың бүйір бетін табанымен қиылыспайтын және өсіне параллел емес жазықтықпен қиғанда шығатын қима эллипс болады.
- Конустың жасаушысы арқылы өтетін, конуспен басқа ортақ нүктелері жоқ жазықтық конусқа жанама жазықтық деп аталадыү (84 сурет)
- Конустың жазбасы және бетінің ауданы
Егер конустың бүйір бетін АВ жасаушысының бойымен қиып жазса, конустың бүйір бетінің жазбасын аламызқ
Сонда біз қандай фигура аламыз? Бұл фигураның ауданын қалай табамыз?
Радиусы R-ге, жасаушысы ι-ге тең конустың бүйір бетінің жазбасы радиусы ι-ге, ұзындығы 2πR болатын дөңгелек сектор аламыз. (85 сурет (2) ) Бұл жазбаның ауданы конустың бүйір бетінің ауданы. Олай болса дөңгелек сектордың ауданының формуласын пайдаланамыз
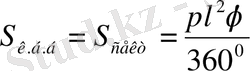
- сектор доғасының бұрыштық шамасы
’
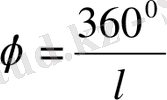
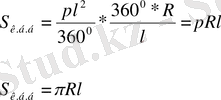
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz