Келтіру формулалары. АШЫҚ САБАҚ

С. Датұлы атындағы № 26 орта мектеп

АШЫҚ САБАҚ
<<Келтіру формулалары>>
9 сынып
Өткізген: Тажиева маншук
Болтасқызы
Атырау 2013

Сабақтың тақырыбы: Келтіру формулалары
Сабақтың мақсаты:
Білімділік: Оқушыларға сүйір бұрыштың тригонометриялық функциясының әрбір бұрышындағы синустыың, косинустың, тангенстің, котангенстің келтіру формулаларымен таныстыру, осы формулаларды тригонометриялық өрнектерді түрлендіруде және есептерді шығару кезінде қолдануды үйрету;
Дамытушылық: Оқушылардың ақыл-ойын дамыту, ойлау қабілетін жетілдіру.
Тәрбиелік: Оқушылардың алгебра пәніне қызығушылығын арттыру, оқушыларды алғырлыққа, шапшандыққа тәрбиелеу.
Сабақта қолданылатын көрнекіліктер: интербелсенді тақта, оқулық, кеспе қағаздар, формула жазылған плакат
Сабақтың әдіс-тәсілдері: көрнекіліктерді қолдану. Әңгімелеу, баяндау.
Сабақтың типі: жаңа сабақ
Сабақ барысы:
І. Ұйымдастыру. Сынып оқушыларының қатысымы. Оқушыларды топқа бөлу, зейінін шоғырландыру.
ІІ. Жаңа сабақ. <<Ой қозғау>>
Егер (мүндағы к- кез келген бүтін сан, α- сүйір бұрыш) бұрышының функциялары берілсе, онда оларды α бұрышына байланысты тригонометриялық функцияларға келтіру ыңғайлы. Ол үшін арнайы берілген келтіру формулаларын қолданамыз.
Енді біз, алдымен ІІ ширектегі синус пен косинус үшін келтіру формулаларын шығарайық.
ОА=R α бұрышына бұрамыз, сосын PI/2+ α бұрамыз. ОА- ОВ-ОВ1 радиусына бұрамыз.

х
у
В1
D1
C1
D
B
C
O
A

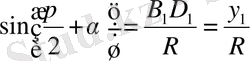
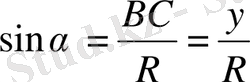
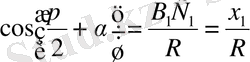
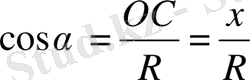
Х
Х
ЕРЕЖЕ
ЕРЕЖЕ

Егер келтірілген тригонометриялық функцияның аргументі (бұрышы) PI+-α (1800+-α), 2PI+-α (3600+-α) түрінде болса, онда оның аты өзгермейді;
Егер келтірілген тригонометриялық функцияның аргументі (900+-α), (2700+-α) түрінде болса, онда синус косинуске, косинус синуске, тангенс котангенске, котангенс тангенске өзгереді;
Келтіру формуласының оң жағының таңбасы сәйкес ширектегі келтірілген функцияның таңбасымен бірдей жазылады;
Келтіру формулалары:

Мысалдар
1) cos73PI мәнін есептейік
cos73PI=cos2PI+PI3=cosPI3=12
2) sin-7800=-sin7800=-sin2∙3600+600=-sin600=-32
ІҮ. Бекіту бөлімі.
1.Оқушыларға сәйкестендіру тесті беріледі (жұптық тапсырма).
tg(PI-α)
cos α
ctg(PI+α)
cos α
sin(360-α)
tgα
cos(360-α)
ctgα
ctg(360-α)
- sinα
tg(360+α)
- ctgα
2.<<Математикалық жәрмеңке>> деп аталатын тур, мұнда топтарға деңгейлік есептер беріледі.
І деңгей
1. 2.
Өрнекті ықшамда:
а)75 ә) 150 б)200 бұрыштарының барлық тригонометриялық функциясын аргументі 45- тан аспайтын функциямен ауыстырыңдар.
ІІ деңгей
ІІІ деңгей
Өрнекті ықшамда:

ЖАУАПТАРЫ:
І деңгей
1. 2.
Өрнекті ықшамда:
ІІ деңгей
ІІІ деңгей
Өрнекті ықшамда:

Оқулықпен жұмыс№334

Ү. Бағалау. Оқушыларды деңгейлік тапсырмаларын орындағанына қарай бағаланады. Яғни барлық деңгейді орындаған оқушыға <<5>> баға, екі деңгейді орындаған оқушыға <<4>> баға, тек бірінші деңгейді орындағаны үшін <<3>> бағамен бағаланады.
ҮІ. Үйге тапсырма:
1. §21- оқу.
2. №329, 331