11-сынып: Анықталған интеграл арқылы жазық фигуралардың ауданын есептеу

Күні:

11-сынып. Алгебра және анализ бастамалары.

11-сабақ.

Тақырып: Анықталған интегралдың көмегімен жазық фигуралардың ауданын есептеу.

Сабақтың мақсаты: Жазық фигуралар туралы түсінік беріп және олардың ауданын табуды оқып-үйрену.

Оқыту мен тәрбиелеудің міндеттері:

Білімділік:Оқушыларға жазық фигуралар, олардың аудандары туралы

ұғым беріп, жазық фигуралардың аудандарын табу бойынша білім, біліктілік дағды-ларын қалыптастыру.

Дамытушылық:Күрделі функциялардың алғашқы функцияларын табу тәсілдерін терең меңгеру, анықталған интегралды есептеуді жете білу біліктілігін дамыту.
Тәрбиелік:Оқушыларды еңбексүйгіштікке, ізденімпаздыққа, ұқыптылыққа баули отырып, математика пәніне деген қызығушылығын арттыру.

Сабақтың көрнектілігі: PowerPoint - презентациялық бағдарлама, интерактивті тақта, таблица-схемалар, оқушы баяндауы, сызба аспаптары.

Сабақ түрі: Аралас сабақ

Оқыту әдіс-тәсілі: Бөлшектеп іздену.

Сабақ барысы:

Ұйымдастыру:(2 минут)

Сәлемдесу.
Журналмен жүмыс.
Оқушылардың сабаққа даярлығын тексеру.
Сабаққа мақсат қою.

Өткен материалды пысықтау(7 минут) .

Оқушы баяндамасы:Презентация -Қисықсызықты трапеция(1-слайд)

Қисық сызықты трапеция

Қисықсызықты трапеция деп - жоғарыдан үзіліссіз, y=f(x) (f(x) >0) функция-сының графигімен, бүйір жақтарынан x=a, x=b және төменнен y=0 түзулерімен шектелген жазық фигураны атайды. Мұндағы абсцисса осінің $\lbrack a; b\rbrack$ кесіндісін - қисықсызықты трапецияның табаны дейді.

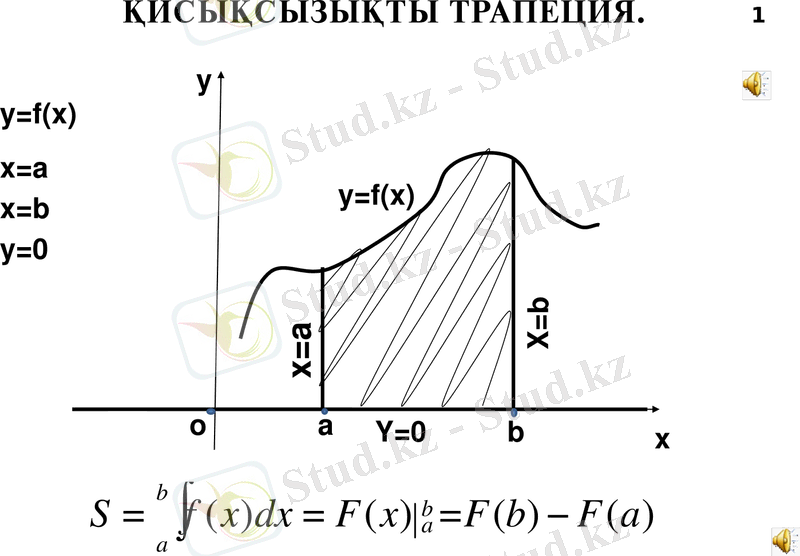
Қисық сызықты трапецияның ауданы(флипчарт1)

Қисықсызықты трапецияның ауданын есептеу үшін S=F(b) -F(a) формуласын қолданады.

Қисықсызықты трапецияның ауданы төмендегідей алгоритм бойынша есептелінеді:

1. Бір координаталық жазықтықта берілген сызықтардың графиктерін салу;

2. Фигураны OX осі бйымен шектелген кесіндісінің шеткі нүктелерін, яғни a және b-ның мәндерін анықтау;

3. f(x) функциясының алғашқы функциясын табу;

4. S=F(b) -F(a) формуласы бойынша қисықсызықты трапецияның ауданын есеп-теу.

Анықталған интеграл. Ньютон-Лейбниц формуласы

F(b) - F(a) айырымын y=f(x) үзіліссіз функциясының $\lbrack a; b\rbrack$ кесіндісіндегі анықталған интегралы деп атайды да, оны былай $\int_{\mathbf{a}}^{\mathbf{b}}{\mathbf{f}\left( \mathbf{x} \right) \mathbf{dx\ \ }}$ белгілейді. Мұнда-ғы a-ны интегралдың төменгі, ал b-ны жоғарғы шегі дейді, ал $f(x) dx\ \$ - интеграл таңбасының астындағы өрнек, x - интегралдау айнымалысы делінеді.

Анықтама бойынша: $\int_{\mathbf{a}}^{\mathbf{b}}{\mathbf{f}\left( \mathbf{x} \right) \mathbf{dx\ \ }}\mathbf{= F}\left( \mathbf{b} \right) \mathbf{- \ F}\left( \mathbf{a} \right) \mathbf{. \ }$ Бұл формула - Ньютон-Лейбниц формуласы деп аталады.

2. Алғашқы функция(анықталмаған интеграл) табу формулалары. (флипчарт2)

Жаңа материалды баяндау:(12 минут)

Жазық фигуралар:Презентация, интерактивті тақта.

Жазық фигуралардың әртүрлі орналасу жағдайлары: (флипчарт-жф1)

o x o x

y y

o x o x

Жазық фигураның ауданын интегралмен есептеу.

y (флипчарт-жф2)

y=f(x)

y=g(x)

О a b X

$s = \int_{a}^{b}{f(x) {dx} -}\int_{a}^{b}{g(x) {dx} = {\int_{a}^{b}\left( f(x) - g(x) \right) dx}}; \ \ Сонымен$

$\mathbf{s =}\int_{\mathbf{a}}^{\mathbf{b}}\left( \mathbf{f}\mathbf{(}\mathbf{x}\mathbf{) }\mathbf{-}\mathbf{g}\mathbf{(}\mathbf{x}\mathbf{) } \right) \mathbf{dx; }$ (1)

1-мысал. y=x ² -2x+4 және y=4 сызықтарымен шектелген фигураның ауданын табайық. (флипчарт-жф3)

y y=x ² -2x+4 (флипчарт-жф3)

A B Y=4

O 1 2 X

x ² -2x+4=4 теңдеуін шешу арқылы графиктердің қиылысу нүктелерінің абсциссаларын табамыз. Олар: x ₁ =0, x ₂ =2. Демек, интегралдау шектері a=0 және b=2.

Штрихталған жазық фигураның ауданын есептеудің екі тәсілін қарастырайық, мұнда f(x) =4 және g(x) = x ² -2x+47

1-тәсіл.

$\mathbf{s =}\int_{\mathbf{0}}^{\mathbf{2}}{\mathbf{(}\mathbf{4}\mathbf{-}\mathbf{x}^{\mathbf{2}}\mathbf{+}\mathbf{2}\mathbf{x}\mathbf{-}\mathbf{4}\mathbf{) }{\mathbf{dx}\mathbf{=}}}\int_{\mathbf{0}}^{\mathbf{2}}{\mathbf{(}\mathbf{2}\mathbf{x}\mathbf{-}\mathbf{x}^{\mathbf{2}}\mathbf{) }{\mathbf{dx}\mathbf{=}}}\left( \mathbf{x}^{\mathbf{2}}\mathbf{-}\left. \ \frac{\mathbf{x}^{\mathbf{3}}}{\mathbf{3}} \right) \right. \ \left\{ \begin{array}{r} \mathbf{2} \\ \mathbf{0} \end{array} \right. \ \mathbf{=}\frac{\mathbf{4}}{\mathbf{3}}\mathbf{(кв. бірл. ) }$

2-тәсіл . OABC тіктөртбұрышының ауданынан OADBC қисықсызықты трапецияның ауданын аламыз: S _Ф =S _OABC -S _OADBC , S _OABC =AB*BC=2*4=8.

$\mathbf{S}_{\mathbf{қ. тр. }}\mathbf{=}\int_{\mathbf{0}}^{\mathbf{2}}{\mathbf{(}\mathbf{x}^{\mathbf{2}}\mathbf{-}\mathbf{2}\mathbf{x}\mathbf{+}\mathbf{4}\mathbf{) }{\mathbf{dx}\mathbf{=}}}\left( \frac{\mathbf{x}^{\mathbf{3}}}{\mathbf{3}} \right. \ \mathbf{-}\mathbf{x}^{\mathbf{2}}\mathbf{+}\left. \ \mathbf{4}\mathbf{x} \right) \left\{ \begin{array}{r} \mathbf{2}\mathbf{\ } \\ \mathbf{0} \end{array} \right. \$ = $\mathbf{\ }\frac{\mathbf{20}}{\mathbf{3}}$ . Сонда S _Ф =8 - $\frac{\mathbf{20}}{\mathbf{3}}\mathbf{=}\frac{\mathbf{4}}{\mathbf{3}}\mathbf{(кв. бірл. ) }$