Сабақ жоспары. Сабақ барысы

Сабақ жоспары

Пән
Сынып
Сабақ №
Мерзімі
Математика
6Ә
119
04.02.17ж.
Тақырыбы:Санды теңсіздіктердің қасиеттері
Мақсаты:Санды теңсіздік туралы мағлұмат беру :
- сандарды салыстырып,теңсіздікпен жазуды;
- қатаң , қатаң емес теңсіздіктерді жазуды,оқуды;
- таңбалары бірдей, таңбалары қарама - қарсы теңсіздіктерді жазуды,оқуды үйрету;
Міндеттері
Қандай әдіс-тәсілдер арқылы іске асырамыз
1.Санды теңсіздік туралы мағлұмат беру :
- сандарды салыстырып,теңсіздікпен жазуды;
- қатаң , қатаң емес теңсіздіктерді жазуды,оқуды;
- таңбалары бірдей, таңбалары қарама - қарсы теңсіздіктерді жазуды,оқуды үйрету;
Мысал келтіру арқылы
2. Есеп шығару арқылы есте сақтау, ойлау қабілеттерін дамыту
Алған білімдерін практикада қолдану арқылы
3. Жауапкершілік, белсенділік, білімге талпыну қасиеттерін бойында тереңдету

Әдістер мен стратегиялар: Практикалық, сұрақ-жауап, жекеше, жұптық, топтық- ұжымдық
Құралдар: оқулық, карточка,бағалау парағы
Сабақ барысы:
Сабақ кезеңдері
Мұғалімнің іс-әрекеттері
Оқушының іс-әрекеттері
Ескерту
1.Ұйымдастыру

2. Үй тапсырмасы тексеру

3.Өткен материалды қайталау

4. Жаңа сабақ

5. Бекіту

6. Инклюзив оқушымен жұмыс

7.Сабақты қорытындылау
Оқушылармен амандасу, түгендеу, назарын сабаққа аудару
Оқушылардың дәптерлерінен үй тапсырмасының орындалуын тексеру
Ынтымақтастық атмосферасы.(2 мин) Балалар, бір - біріңе қарап жымиыңдар, жайланып отырып, көздеріңді жұмыңдар. Менің айтқанымды іштеріңнен қайталаңдар.
Мен бақытты баламын,
Жан дүниемде күн нұрлы
Жылуым мол бойымда.
<<Ыстық орындық>> стратегиясы арқылы
Оқушылар өткен тақырыпқа байланысты бір-бірден сұрақ жазып, конвертке салады. Жеребе арқылы ортаға оқушы шығып, ыстық орындыққа келіп отырып, конверттен сұрақ алады да жауап бере алса, ары қарай жалғастырады, егер жауап бере алмаса, күйіп кетеді де, келесі оқушы шығады.
1) Теңбе-тең өрнектер дегеніміз не?
2)Теңбе-теңдік деп нені атаймыз?
3) Теңбе-тең түрлендіру дегеніміз не?
4)Нелерді пайдаланып, өрнектерді ықшамдаймыз?
5) Сатылы бөлшектер дегеніміз қандай бөлшектер?
6)Тура санды теңдіктің екі жақ бөлігіне де бірдей санды қосқанда тура санды теңдік теңдік шығадыма?
7)Тура санды теңдіктің екі жақ бөлігіне де нөлден өзге бірдей санға көбейткенде немесе бөлгенде тура санды теңдік теңдік шығады ма?
8)Екі тура санды теңдікті мүшелеп қосқанда тура санды теңдік шығады ма?
9)Екі тура санды теңдікті мүшелеп көбейткенде тура санды теңдік шығады ма?
10) Бір айнымалысы бар сызықтық теңдеу дегеніміз не?
11)Теңдеудің түбірі дегеніміз не?
12)Теңдеулерді шешуде қолданылатын теңдеудің қасиеттерін айт!
13)Айнымалысы модуль таңбасының ішінде берілген теңдеу дегеніміз не?
14) Айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеулерді шешудеқандай формулалар қолданылады?
15)Айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеулерді шешуде модульдің қандай қасиеттері қолданылады?
Шешуі:
1)Екі өрнектегі айнымалылардың қабылдайтын мәндерінің кез келгенінде сәйкес мәндері тең өрнектер
2)Айнымалылардың қабылдайтын мәндерінің кез келгенінде тура болатын теңдікті
3)Өрнектегі оған теңбе-тең өрнекпен алмастыруды өрнекті
4)
1)қосудың ауыстырымдылық, терімділік қасиеттерін пайдалану;
2)көбейтудің ауыстырымдылық, терімділік қасиеттерін пайдалану;
3)ұқсас қосылғыштарды біріктіру
4) жақшаларды ашу
5)
1534 және 1-1256 өрнектері - сатылы бөлшектер.
6)Егер а= в болса, онда а+ с= в + с
7)Егер а= в болса, онда ас= в с
8)Екі тура санды теңдікті мүшелеп қосқанда тура санды теңдік шығады.
Мысалы 42:(-6) =-7
12*5=60
42:(-6) + 12* 5= (-7) + 60
53 = 53
9)Екі тура санды теңдікті мүшелеп көбейткенде тура санды теңдік шығады.
5+3 = 8
9-2=7
(5 + 3) * (9-2) = 8*7
10) ах=b түріндегі теңдеу (мұндағы х - айнымалы, ажәне b - қандай да бір сандар) бір айнымалысы бар сызықтық теңдеу деп аталады.
11)теңдеуді тура санды теңдікке айналдырады.
12)1.Теңдеудегіқосылғыштыңтаңбасынқарама - қарсығаөзгертіп, оны теңдеудіңбіржағынанекінші жағына көшіргенде теңдеу мәндес теңдеуге түрленеді.
2.Теңдеуліңекіжағын да нөлденөзгебірдейсанғакөбейткенденемесебөлгендетеңдеумәндестеңдеуге түрленеді.
13)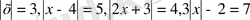теңдеулері айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеулер.
14)Айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеулерді шешуде:
1) координаталық түзудегі A(a) және B(b)нүктелерінің арақашықтығы пайдаланылады:
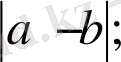
2)
формуласыпайдаланылады.
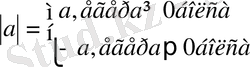
15)Есептеулерде модульдің негізгі қасиеттері де пайдаланылады:

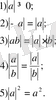
1-қасиет. Егер а саны b санынан үлкен, ал b саны с санынан үлкен болса, онда а саны с санынан үлкен болады.
Егер 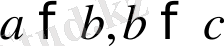болса, онда .
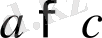2-қасиет. Егер тура теңсіздіктің екі жақ бөлігіне де бірдей сан қосылса, теңсіздік белгісі өзгертілмей, тура санды теңсіздік шығады.
Егер 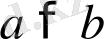болса, онда .
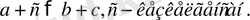3-қасиет. Егер тура теңсіздіктің екі жақ бөлігі бірдей оң санға көбейтілсе немесе бөлінсе, теңсіздік белгісі өзгертілмей, тура санды теңсіздік шығады.
Егер болса, онда .
Егер тура теңсіздіктің екі жақ бөлігі бірдей теріс санға көбейтілсе немесе бөлінсе және қарама-қарсы таңбаға өзгертілсе, тура санды теңсіздік шығады.
Егер болса, онда .
4-қасиет. Егер теңсіздік белгілері бірдей тура теңсіздіктер мүшелеп қосылса, онда теңсіздік белгісі қосылғыш теңсіздіктердің белгілеріндей тура теңсіздік шығады.
Егер болса, онда
5-қасиет. Теңсіздік белгілері бірдей және оң жақ бөлігі мен сол жақ бөлігі оң сандар болатын тура теңсіздіктерді мүшелеп көбейтуге болады. Нәтижесінде теңсіздік белгісі көбейткіш теңсіздіктердің белгісіндей тура теңсіздік шығады.
Егер болса, онда
6-қасиет.
Егер болса, онда

№957

№958

№959

№960

№961

№963

Үйге тапсырма:№ 947 ,№ 948,954
Бағалау. Оқушылардың белсенділіген байланысты бағаланады.
Жинақталады, сабаққа ынталанады.
Үй тапсырмасының дұрыстығын тексереді

Алған білімдерін еске түсіреді.

Алған білімдерін түрлендіріп есеп шығаруда пайдалану.

Оcы тапсырмаларды орындау үшін
алған білімдерін түрлендіріп пайдалану, оқушының ойлау қабілетін жетілдіреді.

Оқушының
ойлау қабілетін жетілдіреді.

Тексерілді: