Жанаманың теңдеуі

Пәні
Алгебра және анализ бастамалары
Класс
11
Күні
18.05.
Тақырыбы
Функцияның графигіне жүргізілген жанаманың теңдеуі
Мақсаты
Практикалық іс-әрекетте қолдана алу үшін <<Жанаманың теңдеуі>> тақырыбы бойынша білім мен біліктерін қалыптастыруды жалғастыру; танымдық іс-әрекеттерін дамыту үшін компьютер мен мультимедианы қолданудағы дағдыларын дамыту; алгоритмдік мәдениет, логикалық ойлау, сыни тұрғыда ойлауларын дамыту.
Оқыту нәтижесі
А: Практикалық тапсырмалар орындайды
В: Зерттеу жұмысын орындайды, қорытынды жасайды, алгоритм құрады
С: Жанаманың теңдеуі көмегімен шығарылатын тапсырмалар орындайды
Оқытуда қолданылатын
әдіс-тәсілдер
Топтық жұмыс; Сұрақ-жауап; СТО (ой қозғау); Зерттеу жұмысы; Рефлексия.
Ресурстар
Суреттер, дидактикалық тапсырмалар, кеңейтілген тапсырмалар
Бағалау
Критерийлер бойынша топтық және өзін-өзі бағалау.
Этаптары
Мұғалім
іс-әрекеті
Оқушы
Іс-әрекеті
І.Кіріспе
4 мин
Сабақтың мақсатын айқындау
1.Туындының геометриялық мағынасы қандай?
2.a;b интервалында y=fx функциясының графигіне х0 нүктесінде жанама жүргізілуі үшін қандай шарт орындалу керек?
3.Жанаманың теңдеуін жазыңдар.

ІІ.Тұсаукесер
Сұрақ-жауап
8 мин

1.Қай функцияның графигіне х=3 нүктесінде жанама жүргізуге болады?
2.y=fx функциясының графигіне х1, х2, х3, х4 нүктелерінде жанамалар жүргізілген. Неше нүктеде туынды оң мән қабылдайды?
3.Суретте функциялар графиктері мен оларға а нүктесінде жүргізілген жанамалар берілген. Қай функцияның туындысы а нүктесінде 1-ге тең?
4. Суретте (-4;9) аралығындағы у=f(x) функциясының туындысы берілген. Абсцииса осіне параллель болатын функция графигіне жүргізілген жанамалар саны нешеу?
5. Қай нүктеде функция графигіне жанама бұрыштық коэффициент ең кіші мән қабылдайды?
6. у=f(x) функциясының графигіне у=2х+5 түзуіне параллель болатын барлық жанамалардың жанасу нүктелерін көрсетіңдер.
7. y=f(x) функциясы графигіне х=5 нүктесінде жүргізілген жанама координаттар басы арқылы өтеді. Бұрыштық коэффициентті табыңдар.
8. Параболаға қай нүктелерде а)2, ә)3,б)1, в)0 жанама жүргізуге болады?

Сұрақтарға жауап береді, жауаптарын негіздейді
1.а
0.2 мен 3
3.Б
4.3
5.-1
0.4 нүкте
7.3/5
8.а) x=1, y<-7,
ә) мүмкін емес,
б)у<=х2-2х-6, у>=-7,
в)у>х2-2х-6

ІІІ.Мағынаны тану
1.Зерттеу жұмысы
<<Гипербола және оған жүргізілген жанама>>
15 мин

3.Топтық жұмыс. Практикалық тапсырмалар
10 мин

Тақырыбы: <<Жанаманың теңдеуі>>
Зерттеу нысаны: <<Гипербола және оған жүргізілген жанама>>
Мақсаты: Гиперболаға жүргізілген жанаманың қасиеттерін анықтау
1.Мастер функций бағдарламасымен жұмыс. Жанаманың теңдеуін тұрғызу, жанаманың координаталық осьтермен қиып түсіретін үшбұрыштың ауданын есептеу, кестеге толтыру
2.Гипотеза/Болжам/
3.Дәлелдеу

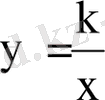
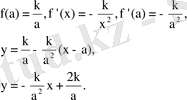
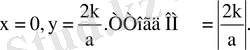
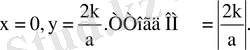
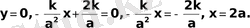
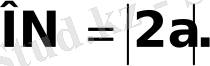
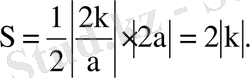
4.Қорытындылар
5.Анықталған фактілерді қолдану. Алгоритм құру

1-топ.
№1. fx=x3+27 функциясының графигіне x0=-3 нүктесінде жүргізілген жанаманың көлбеулік бұрышын табыңдар.
№2. fx=5-12х2функциясының графигіне x0=3 нүктесінде жүргізілген жанаманың теңдеуін жазыңдар, сызбасын орындаңдар.
№3. y=0.5x+0.5 түзуі y=x функциясы үшін жанама бола ма?
№4. y=x33 функцияның графигіне жүргізілген жанама y=4х-7 түзуіне параллель. Жанаманың теңдеуін жазыңдар.
2-топ.
№1. Қай нүктелерде fx=3x2-12х+7 функциясының графигіне жүргізілген жанама ОХ осіне параллель болады?

№2. fx=х2-4 функциясының графигіне x0=-2 нүктесінде жүргізілген жанаманың теңдеуін жазыңдар, сызбасын орындаңдар.
№3. y=12x-10 түзуі y=4х3 функциясы үшін жанама бола ма?
№4. Координаттар басы арқылы өтетін түзу y=fx функциясын А(-7; 14) нүктесінде жанайды. f/-7 есептеңдер.
3-топ.
№1. Қай нүктеде y=x функциясының графигіне жүргізілген жанама абсциссалар осімен 600 бұрыш жасайды?
№2. fx=х-1х2 функциясының графигіне y=3х түзуіне параллель болатын жанаманың теңдеуін жазыңдар.
№3. y=х түзуі y=sinх функциясы үшін жанама бола ма?
№4. 3. fx=х33-3log37-x функциясының графигіне қандай нүктелерде жүргізілген жанамалар y=65х функциясына параллель болады?
1.Кестеге мәндерді толтырады, үшбұрыш ауданын есептейді
2.Гиперболаға х=а нүктесінде жүргізілген жанамамен қиып түсетін үшбұрыштың ауданы тұрақты
3. Дәлелдеуді тақтада бірге орындау
4.Қорытындылар:
-у=k/x гиперболасына х=а нүктесінде жүргізілген кез келген жанама координаттар осінен аудандары 2|k|-ға тең бірдей үшбұрыштар қиып түсіреді
-гиперболаға жүргізілген жанаманың координаттар осьтері арасындағы бөлігі жанасу нүктесінде қақ бөлінеді
-Жанасу нүктесі жанамамен координаттар осьтерінен қиып түсірген үшбұрышқа сырттай сызылған шеңбердің центрі болады
5. у=k/x функциясының графигіне кез келген нүктеде жүргізілген жанаманы тұрғызу алгоритмін құрады

ІҮ.Қорытынды
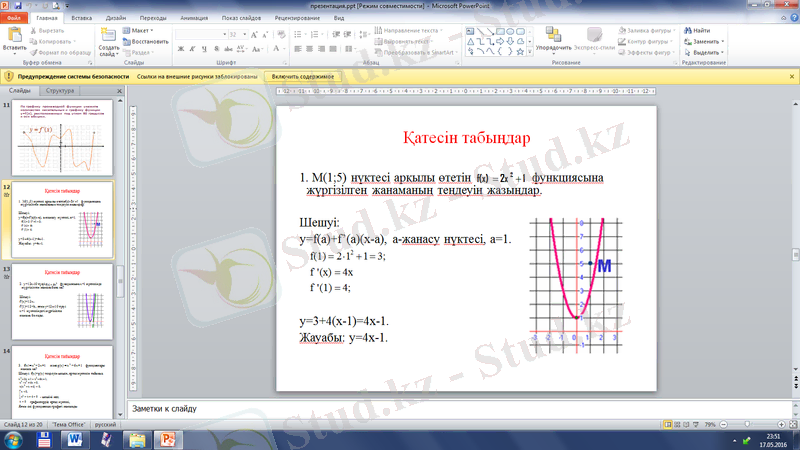
<<Қатесін тап>>
5 мин

Бағалау
3 мин

Жауап парағындағы критерийлер бойынша бағаланады

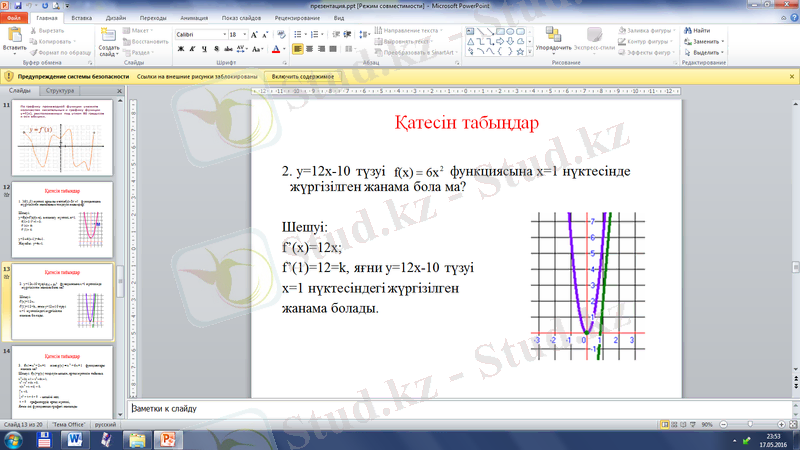
Жауабы: (1;5) нүктесі функцияға тиісті емес.

Жауабы: болмайды, себебі түзу мен функция графигінің ортақ нүктесі жоқ

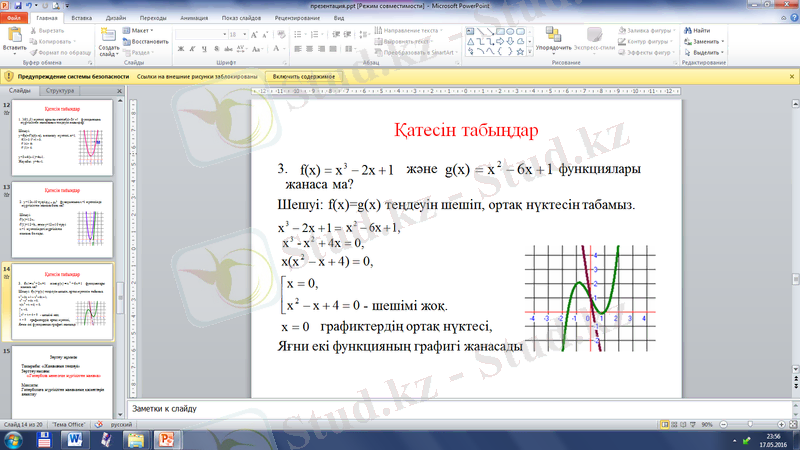
Жауабы: графиктердің ортақ нүктесі - қиылысу нүктесі де болуы мүмкін. Екі функция қиылысады

Рефлексия

1-топ.
№1. fx=x3+27 функциясының графигіне x0=-3 нүктесінде жүргізілген жанаманың көлбеулік бұрышын табыңдар.

№2. fx=5-12х2функциясының графигіне x0=3 нүктесінде жүргізілген жанаманың теңдеуін жазыңдар, сызбасын орындаңдар.

№3. y=0.5x+0.5 түзуі y=x функциясы үшін жанама бола ма?

№4. y=x33 функцияның графигіне жүргізілген жанама y=4х-7 түзуіне параллель. Жанаманың теңдеуін жазыңдар.

2-топ.
№1. Қай нүктелерде fx=3x2-12х+7 функциясының графигіне жүргізілген жанама ОХ осіне параллель болады?

№2. fx=х2-4 функциясының графигіне x0=-2 нүктесінде жүргізілген жанаманың теңдеуін жазыңдар, сызбасын орындаңдар.

№3. y=12x-10 түзуі y=4х3 функциясы үшін жанама бола ма?

№4. Координаттар басы арқылы өтетін түзу y=fx функциясын А(-7; 14) нүктесінде жанайды. f/-7 есептеңдер.

3-топ.
№1. Қай нүктеде y=x функциясының графигіне жүргізілген жанама абсциссалар осімен 600 бұрыш жасайды?

№2. fx=х-1х2 функциясының графигіне y=3х түзуіне параллель болатын жанаманың теңдеуін жазыңдар.

№3. y=х түзуі y=sinх функциясы үшін жанама бола ма?

№4. 3. fx=х33-3log37-x функциясының графигіне қандай нүктелерде жүргізілген жанамалар y=65х функциясына параллель болады?

Зертеу жұмысы
Тақырыбы: <<Жанаманың теңдеуі>>
Зерттеу нысаны: <<Гипербола және оған жүргізілген жанама>>

Мақсаты: Гиперболаға жүргізілген жанаманың қасиеттерін анықтау

1.Мастер функций бағдарламасымен жұмыс. Жанаманың теңдеуін есептеу, жанаманың координаталық осьтермен қиып түсіретін үшбұрыштың ауданын есептеу, кестеге толтыру

Жанасу нүктесінің абсциссасы
у=k/x функциясына жүргізілген жанаманың теңдеуі
Үшбұрыш ауданы
1
а=1

2
а=2

3
а=4

4
а=8

5
а=-1

6
а=-2

7
а=-4

8
а=-8

2.Гипотеза/Болжам/

3.Дәлелдеу
4.Қорытындылар

5. у=k/x функциясының графигіне кез келген нүктеде жүргізілген жанаманы тұрғызу алгоритмін құрыңдар

Бағалау парағы
1-топ
№
Аты-жөні
Үй жұмысы
Сұрақтар
Зерттеу жұмысы
Есеп шығару
Қатесін тап
Баллы
Бағасы
1

2

3

4

5

Бағалау парағы
2-топ
№
Аты-жөні
Үй жұмысы
Сұрақтар
Зерттеу жұмысы
Есеп шығару
Қатесін тап
Баллы
Бағасы
1

2

3

4

5

Бағалау парағы
1-топ
№
Аты-жөні
Үй жұмысы
Сұрақтар
Зерттеу жұмысы
Есеп шығару
Қатесін тап
Баллы
Бағасы
1

2

3

4

5

6