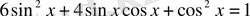Тригонометриялық теңдеулерді шешу: математика пәні бойынша әдістемелік өңдеу (Түркістан медициналық колледжі)


ТҮРКІСТАН МЕДИЦИНА КОЛЛЕДЖІ
№12 ФИЗИКА, МАТЕМАТИКА ЖӘНЕ ТУЫСТАС ПӘНДЕР БОЙЫНША
ЦИКЛДІК ӘДІСТЕМЕЛІК КОМИССИЯСЫ
МАТЕМАТИКА ПӘНІНЕН АШЫҚ САБАҚҚА
АРНАЛҒАН ӘДІСТЕМЕЛІК ӨҢДЕУ

Сабақтың тақырыбы:
Тригонометриялық теңдеулерді шешу

Мамандық : 0302033 «Мейірбике ісі»
Біліктілік : 0302033 «Жалпы тәжірибелі мейірбике»
Дайындаған математика пәнінің
оқытушысы: Амиров Н. О.
Сабақтың тақырыбы: Тригонометриялық теңдеулерді шешу
Уақыты: 90 мин.
Тобы: I курс, М-102 топ
Сабақтың түрі: Жаңа білімді меңгеру сабағы
Сабақтың педагогикалық мақсаты:
- Студенттердің өз беттерінше іздену жұмыстары арқылы кәсіптік шеберліктерін жетілдіруге, ғылыми көзқарасын қалыптастыруға ықпал ету;
- Кәсіби бағдар беру, ғылыми жобалау, дамыта оқыту, ақпараттық технологияларды қолдану арқылы білім берудің сапасын арттыру;
- Интерактивті технология әдісі қолданудың маңыздылығын көрсету;
- Студенттердің өз беттерінше іздену жұмыстары арқылы кәсіптік шеберліктерін жетілдіруге, ғылыми көзқарасын қалыптастыруға ықпал ету;
- Интерактивті тақтаны қолдану арқылы студенттердің белсенділігі мен қызығушылығын арттыру;
- Студенттерге тақырыптың басқа пәндермен байланысын көрсету, пәнаралық және пәнішілік байланысты тереңдету;
- Ұжымдық жұмыс этикасын дамыту;
- Мамандығына деген қызығушылығын ояту.
Сабақтың мақсаты:
Білімділік:
- Білімді қалыптастыру, студенттерді интегралдан хабардар етіп қана қоймай, интегралдың қасиеттерін білу, формулаларын, алған білімдерін есеп шығару барысында дұрыс қолдануға үйрету;
- Студенттерді математикалық тілде сөйлеуге үйрету, өз бетінше жұмысына сараптама жүргізіп үйрету.
Дамытушылық:
- Жеке тұлғаны, жалпы қабілеттерін, талдау, салыстыра білу, негізсізін ажырата білу, керек формулаларды дұрыс қолдана білуге машықтандыру, шыдамдылық, төзімділік қасиеттерін дамыту;
- Студенттердің логикалық ойлау қабілеттерін, алғырлығын, тапқырлығын, шығармашылық қабілеттерін дамыту, өз бетінше шешім қабылдауға дағдыландыру, есте сақтау қабілеттерін дамыту.
Тәрбиелік:
- Адамгершілік, патриоттық тәрбие беру;
- Еңбекке баулу;
- мамандыққа бағдарлау.
Студент білуі керек:
- Тригономнтриялық теңдеулердің түрлері
- Тригономнтриялық теңдеулерді шешу ережелерін;
- Негізгі тригонометриялық формулаларды;
- Кері тригонометриялық функцияларды;
- Тригонометриялық теңдеулерді тиімді әдістермен шешуді үйрену;
Студент істей алуы керек:
- Тригонометриялық теңдеулерді шешу әдістерін;
- Тригонометриялық теңдеулерді тиімді әдістермен шешуді.
Сабақ барысында қолданылатын педагогикалық технологиялар:
- Дамыта оқыту;
- Интерактивті технология;
- Интеграциялық технология;
- Деңгейлеп оқыту;
- Ақпараттық-коммуникациялық оқыту технологиясы;
- Кәсіптік бағдар беру технологиясы.
Берілген әдістерді іске асыру:
Интерактивті тақтамен жұмыс, жазбаша жұмыс, проблемалық жағдай туғызу, жаттығу, пысықтау, сараптау, саралау, оқулықпен жұмыс, жаттығу, түсіндіру, көрсету, өз бетімен жұмыс орындау, ой шақыру, есеп шығару, жекелей және топпен жұмыс.
Пәнішілік байланыс:
Құзіреттілік аймағы В Функция, оның түрлері. Функцияның графиктері.
Оқыту модулі В4 Шек туралы теоремалар.
Оқыту модулі Г2 Функцияның шексіздіктегі шегі. 2 тамаша шек.
Құзіреттілік аймағы Д Тригонометриялық функциялар.
Оқыту модулі Д1 Сандық аргументтің тригонометриялық функциялары,
олардың қасиеттері.
Оқыты модулі Д2. Тригонометриялық функциялардың қасиеттері мен графиктері.
Оқыту модулі Д3. Кері тригонометриялық функциялар.
Оқыту модулі Д4. Біртекті тригонометриялық функциялардың қосындысы мен
айырмасының формулалары.
Оқыту модулі Д 6 Тригонометриялық функцияларды тепе-тең түрлендіру.
- Пәндер аралық байланыс (қамтитын, қамтылатын пәндер)
Қамтитын пәндер:
Қамтылатын пәндер:
Сабақтың жабдықталуы:
 Көрнекті құралдар:
Көрнекті құралдар:
- Формулалар;
- Слайдтар.
Үлестірме материалдар:
- тест;
- жұмыс дәптері;
- деңгейлік есептер.
Техникалық оқу құралдары:
- CD, DVD дискілер;
- Сұйық кристалды LCD теледидары;
- Интерактивті тақта, компьютер;
Қолданылған негізгі әдебиеттер
1. Алгебра және анализ бастамалары 10-11 сынып, Колмогоров А. Н, Алматы 1994 ж.
2. Жоғарғы математика, Әубәкір С. Б, Алматы 2004 ж.
3 . Алгебра 10 сынып, А. Е Әбілқасымова, В. Е. Корчевский, К. Д. Шойынбекова З. А. Жұмағұлова, Алматы 2009 ж.
4. Алгебра 11 сынып, Н. Я. Виленкин, О. С. Ивашев-Мусатов, Москва 2002 г.
Қосымша әдебиеттер
1. Алгебра 8 сынып, А. Әбілқасымова, И. Бекбоев, А. Абдиев, З. Жұмағұлова, Алматы 2008 ж.
2. Алгебра 9 сынып, А. Әбілқасымова, И. Бекбоев, А. Абдиев. З, Жұмағұлова, Алматы 2009 ж.
3. Алгебра и начало анализа, А. Н. Колмогоров, Москва 1993 г.
 4. Шың баспасының анықтамалықтары.
4. Шың баспасының анықтамалықтары.
5. Түрлі баспалардың анықтамалықтары.
WEB сайттар тізімі
1. www. maths. kz
2. www. ustaz. kz
3. kk. wikipedia. org
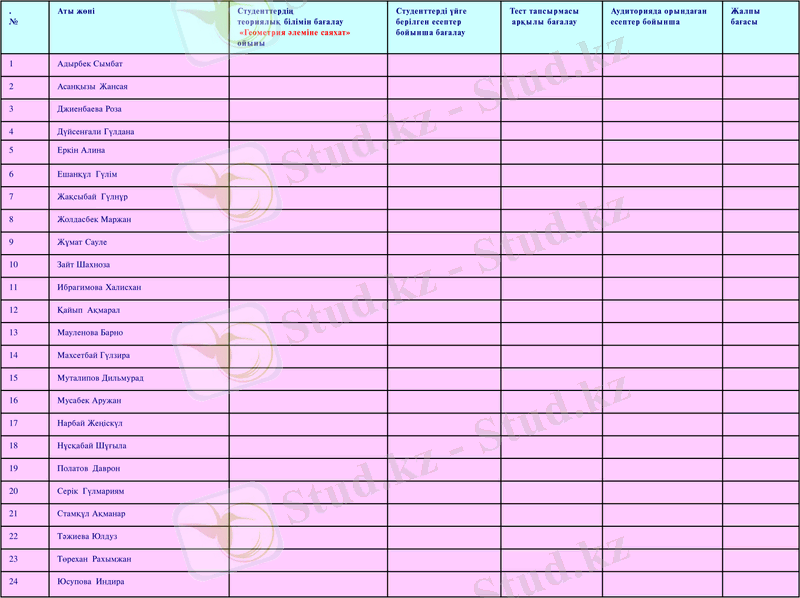
Сабақ жоспары мен хронокартасы
Сабақтың барысы:
1 Ұйымдастыру кезеңі (2-3 минут) - Студенттерді түгелдеу, аудитория тазалығына, студенттердің сырт келбетіне көңіл бөлу. Сабаққа қажетті құрал-саймандары мен бор және тақта сүрткіштің бар болуын қадағалау. Журналды толтыру.
2 Сабақтың мақсаты мен жоспарын хабарлау (2-3 мин) - Тақырыпқа мотивациялық, сипаттама беру, маңыздылығын түсіндіру. Студенттерді сабақтың жоспарымен және бағалау критерийлерімен таныстыру.
3 Үй жұмысын тексеру, студенттердың білімдерін бақылау (20 мин) - Студенттің білімін бақылайтын сұрақтар, есептердің барлығын және 2 нұсқа тест сұрақтары арқылы тексеру .
Сұрақтар:
- Қосу формуласы не үшін қолданылады? (есептерді ықшамдап шығару үшін)
Екі бұрыштың айырымның косинусының формуласын көрсетіңіз? (
)
- Екі бұрыштың айырымның синусының формуласын көрсетіңіз?()
Екі бұрыштың қосындысы мен айырымның тангенсының формуласын көрсетіңіз?
(
)
- Келтіру формулалары не үшін қолданылады?(егербұрышының
функциялары берілсе, онда оларда
бұрышына байланысты тригонометриялық функцияларға келтіру ыңғайлы.
Қос бұрыштың формулалары қалай алынады? (Қос бұрыштың формулалары қосу
формуларындағы
мен
бұрыштарын
аламыз)
- Арксинус дегеніміз не?(аралығында синусыa-ға тең сана санының арксинусыдеп аталады. )
Арксинустың анықталу облысы? (
кесіндісі )
Арксинустың мәндерінің облысы? (-
кесіндісі)
- Арккосинустың анықталу облысы?(кесіндісі)
Арккосинустың мәндерінің облысы? (
кесіндісі )
- Арккотангенс деген не?(аралығындағы котангенсі а-ға тең сана санының арккотангенсідеп аталады)
Арктангенстың анықталу облысы? ( барлық нақты сандар жиыны )
Арктангенстың мәндерінің облысы? (
аралығы)
- Екі бұрыштың қосындысының косинусының формуласын көрсетіңіз?()
- Екі бұрыштың қосындысының синусының формуласын көрсетіңіз?()
- Тангентің анықталу облысы?( D(tg ) x =аралығы)
Арктангенстың анықталу облысы? ( барлық нақты сандар жиыны )
- Тангенс дегеніміз не? ( у=tg x формуласымен берілген сандық функция)
Котангенс дегеніміз не? (у=сtg x формуласымен берілген сандық функция)
11.
Синус және косинус функцияларының мәндер облысы қандай?
(
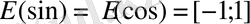 )
)
Синус және косинус функцияларының анықталу облысы қандай? (
)
12. Синус дегеніміз не? (у=sin x формуласымен берілген сандық функция)
Косинус дегеніміз не? (у=cos x формуласымен берілген сандық функция)
үйге берілген есептерді тексеру (сканерлеп)
№ 24.
в)
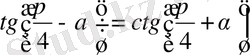
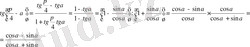
г)
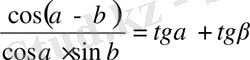

№ 27.
в)

г)

№ 90.
в)
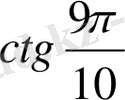 ,
,
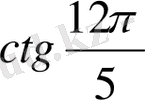 ,
,
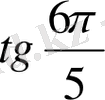 ,
,
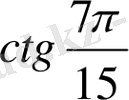
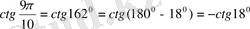
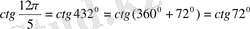
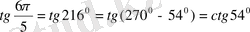

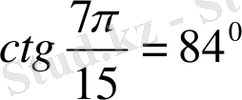
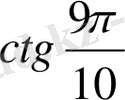 ,
,
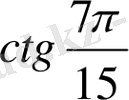 ,
,
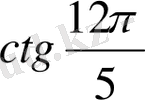 ,
,
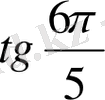
г)
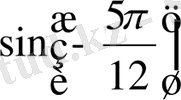 ,
,
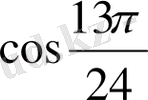 ,
,
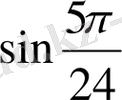 ,
,
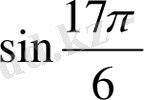
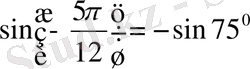
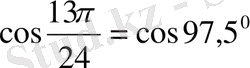
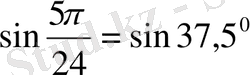
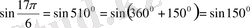
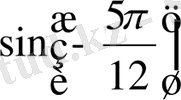 ,
,
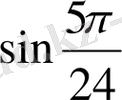 ,
,
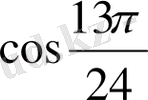 ,
,
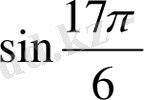
Тест тапсырмасы:
Тест 1-вариант
1. Теңдеу
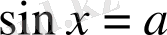 түрінде берілсе, онда шешім:
түрінде берілсе, онда шешім:
а)
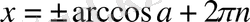
 b)
b)
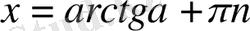
 c)
c)
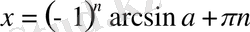

d)
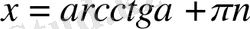
 e)
e)
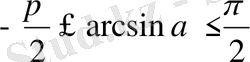
2. Теңдеу
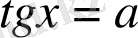 түрінде берілсе, онда шешім:
түрінде берілсе, онда шешім:
а)
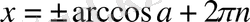
 b)
b)
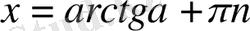
 c)
c)
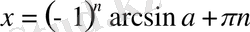

d)
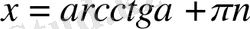
 e)
e)
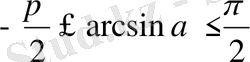
3. Теңдеу
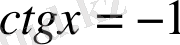 түрінде берілсе, онда шешім:
түрінде берілсе, онда шешім:
а)
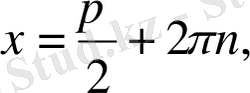
 b)
b)
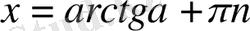
 c)
c)
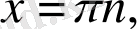

d)
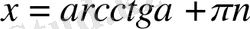
 e)
e)
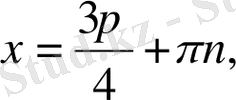

4. Теңдеу
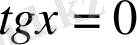 түрінде берілсе, онда шешім:
түрінде берілсе, онда шешім:
а)
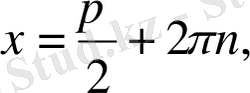
 b)
b)
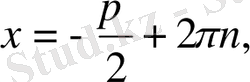
 c)
c)
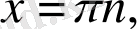

d)
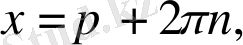
 e)
e)
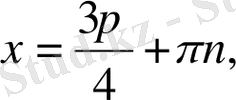

5. Теңдеу
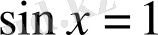 түрінде берілсе, онда шешім:
түрінде берілсе, онда шешім:
а)
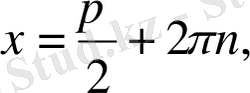
 b)
b)
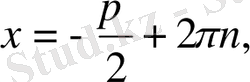
 c)
c)
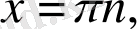

d)
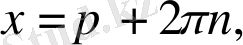
 e)
e)
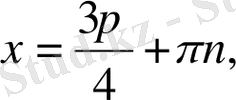

6. Теңдеу
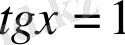 түрінде берілсе, онда шешім:
түрінде берілсе, онда шешім:
а)
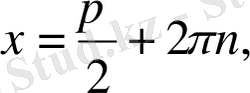
 b)
b)
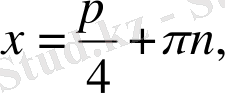
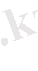
 c)
c)
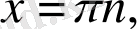
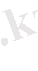

d)
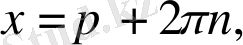
 e)
e)
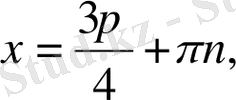

7. Арктангенс және арккотангенс функцияларының анықталу облысы:
- R b) c) d) e)
8.
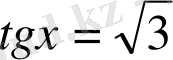 теңдеуін шешіңіз:
теңдеуін шешіңіз:
а)
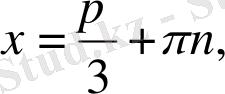
 b)
b)
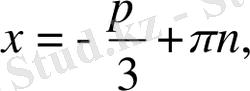
 c)
c)
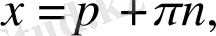

d)
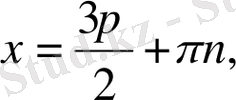
 e)
e)
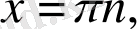

9.
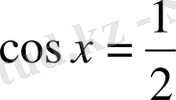 теңдеуін шешіңіз:
теңдеуін шешіңіз:
а)
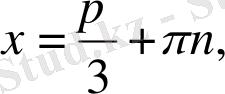
 b)
b)
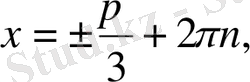
 c)
c)
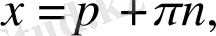

d)
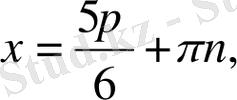
 e)
e)
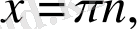

10.
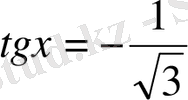 теңдеуін шешіңіз:
теңдеуін шешіңіз:
а)
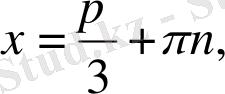
 b)
b)
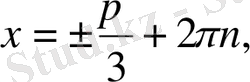
 c)
c)
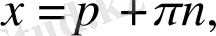

d)
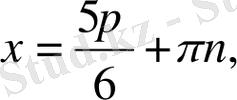
 e)
e)
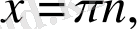
 Тест тапсырмасы:
Тест тапсырмасы:
Тест 2-вариант
1. Теңдеу
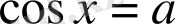 түрінде берілсе, онда шешім:
түрінде берілсе, онда шешім:
а)
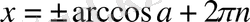
 b)
b)
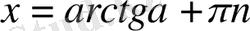
 c)
c)
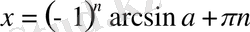

d)
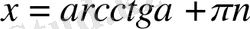
 e)
e)
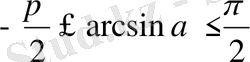
2. Теңдеу
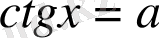 түрінде берілсе, онда шешім:
түрінде берілсе, онда шешім:
а)
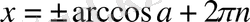
 b)
b)
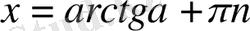
 c)
c)
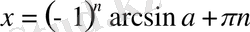

d)
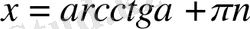
 e)
e)
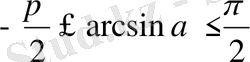
3. Теңдеу
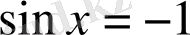 түрінде берілсе, онда шешім:
түрінде берілсе, онда шешім:
а)
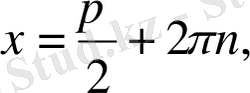
 b)
b)
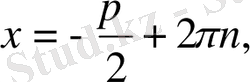
 c)
c)
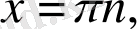

d)
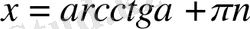
 e)
e)
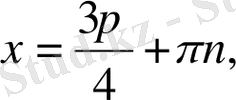

4. Теңдеу
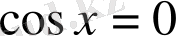 түрінде берілсе, онда шешім:
түрінде берілсе, онда шешім:
а)
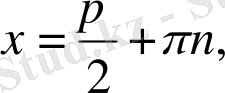
 b)
b)
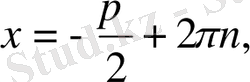
 c)
c)
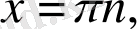

d)
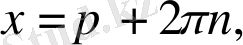
 e)
e)
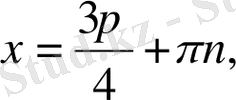

5. Теңдеу
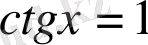 түрінде берілсе, онда шешім:
түрінде берілсе, онда шешім:
а)
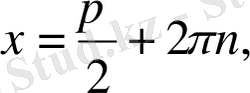
 b)
b)
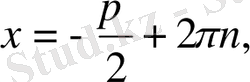
 c)
c)
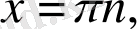
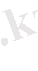

d)
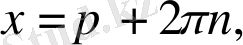
 e)
e)
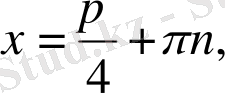

6. Теңдеу
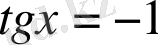 түрінде берілсе, онда шешім:
түрінде берілсе, онда шешім:
а)
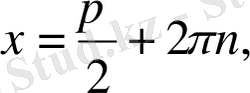
 b)
b)
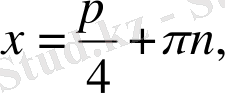
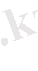
 c)
c)
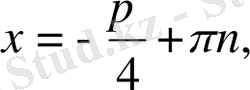

d)
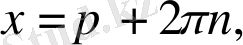
 e)
e)
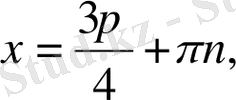

7. Синус және косинус функцияларының мәндерінің облысы:
- R b) c) d) e)
8.
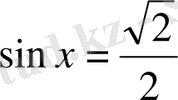 теңдеуін шешіңіз:
теңдеуін шешіңіз:
а)
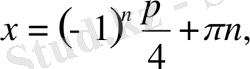
 b)
b)
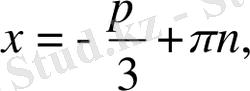
 c)
c)
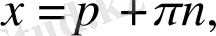

d)
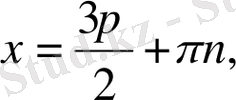
 e)
e)
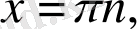

9.
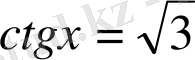 теңдеуін шешіңіз:
теңдеуін шешіңіз:
а)
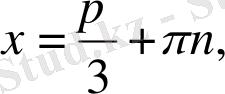
 b)
b)
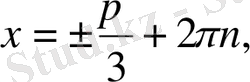
 c)
c)
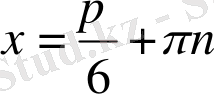

d)
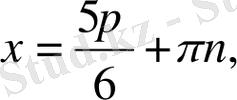
 e)
e)
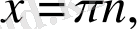

10.
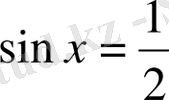 теңдеуін шешіңіз:
теңдеуін шешіңіз:
а)
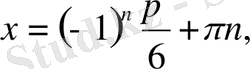
 b)
b)
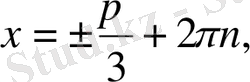
 c)
c)
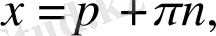

d)
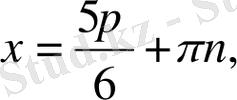
 e)
e)
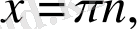

Тесттің дұрыс жауаптары:
Бағалау критериі:
9-10- «5»
7-8 - «4»
5-6 - «3»
5↓ - «2»
4 Баға қою және түсінік беру (5 мин) - Үй тапсырмасы бойынша сұрақтар, есептер және тақырыпқа сай берілген тест жинағы бойынша бағалау.
Студенттерді бағалау критериі:
5. Жаңа тақырыпқа мотивациялық сипаттама беріп, тақырыпты түсіндіру (25-30 мин) -
Бүгінгі сабағымыз « Тригонометриялық теңдеулерді шешу» тақырыбында
өтеді. Күрделі тригонометриялық теңдеулерді шешудің тиімді әдістерін қарастырамыз. Тригонометриялық теңдеулерді шешу үшін кері тригонометриялық функцияларды, тригонометриялық формулаларды, негізгі тригонометриялық теңбе-теңдіктерді, қос аргументтің формулаларын, тригонометриялық функциялардың мәндерін білуіміз, тригонометриялық функциялардың мәндер кестесін пайдалана білуіміз керек.
Сабақтың тезистері:
- Тригонометриялық теңдеулерді шешу.
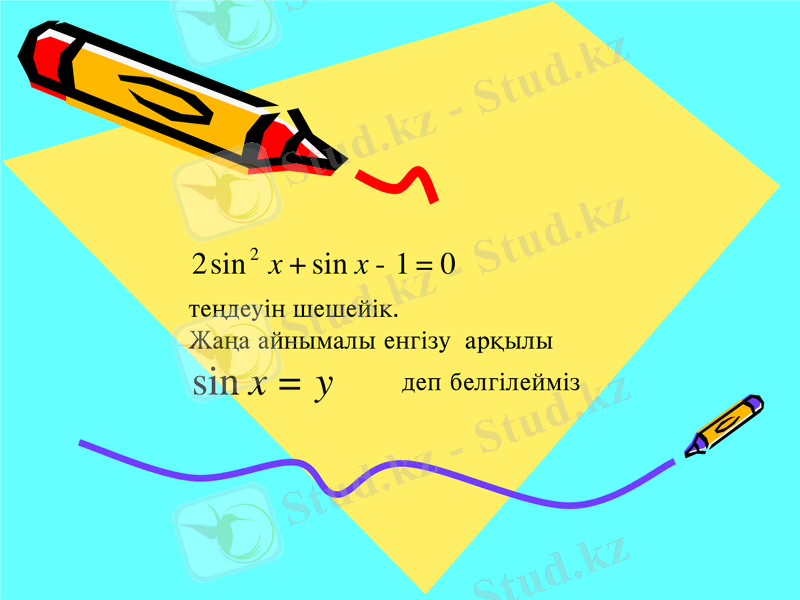
Күрделі тригонометриялық теңдеулерді шешуде біз көбінесе оларды ықшамдап есептейміз. Ол үшін біз берілген теңдеуге жаңа айнымалы енгізу әдісі арқылы есептейміз. Жаңа айнымалы енгізіп, ол теңдеуді қарапайым тригонометриялық теңдеуге келетінін көреміз. Ол әдістерді төмендегі мысалдар түрінде көрсетейік:
- мысал. теңдеуін шешейік.
Жаңа айнымалы енгізу арқылы
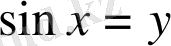 деп белгілейміз.
деп белгілейміз.
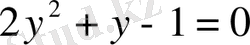
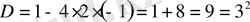
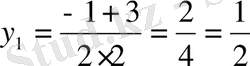
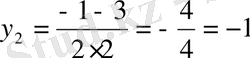
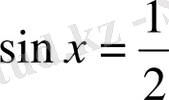
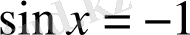
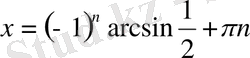 ,
,

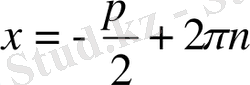 ,
,

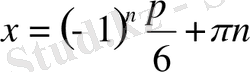 ,
,

2-мысал.
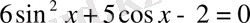 теңдеуін шешейік:
теңдеуін шешейік:
 теңдігінен
теңдігінен
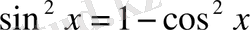
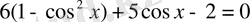
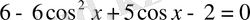
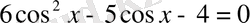
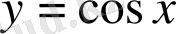
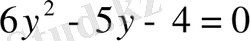
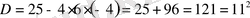
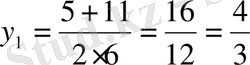
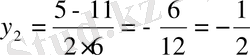
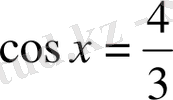
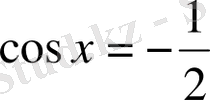
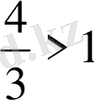 шешімі жоқ
шешімі жоқ
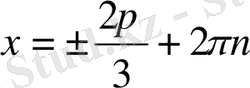 ,
,

3-мысал.
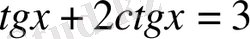
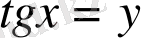
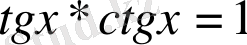
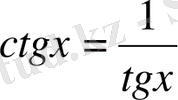
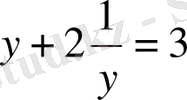
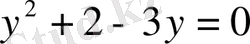
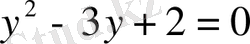
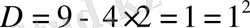
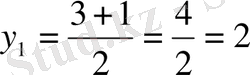
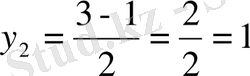
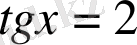
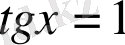
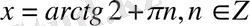
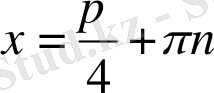 ,
,

4-мысал.
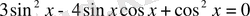 /
/
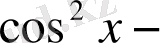 қа бөлеміз. Сонда
қа бөлеміз. Сонда
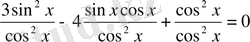
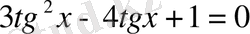
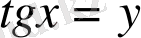
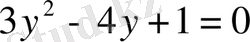
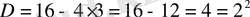
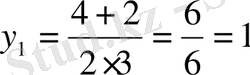
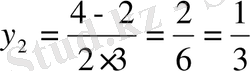
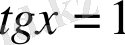
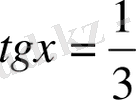
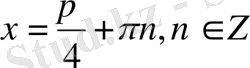
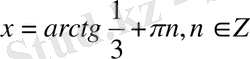
5-мысал.
 теңдігін пайдаланып,
теңдігін пайдаланып,
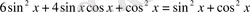
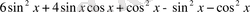
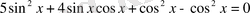 /
/
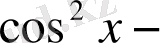 қа бөлеміз. Сонда
қа бөлеміз. Сонда
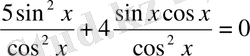
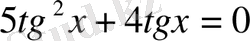
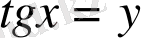
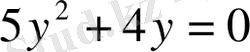 - толымсыз квадрат теңдеу
- толымсыз квадрат теңдеу
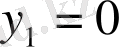
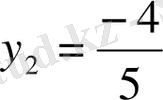
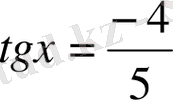
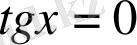
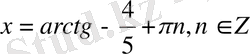
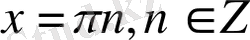
6-мысал.
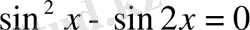
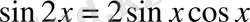
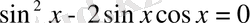
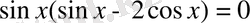
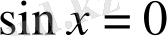
(сosx-қа бөлеміз)
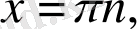
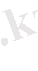

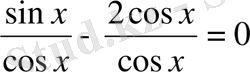
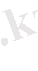
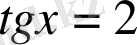
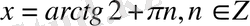
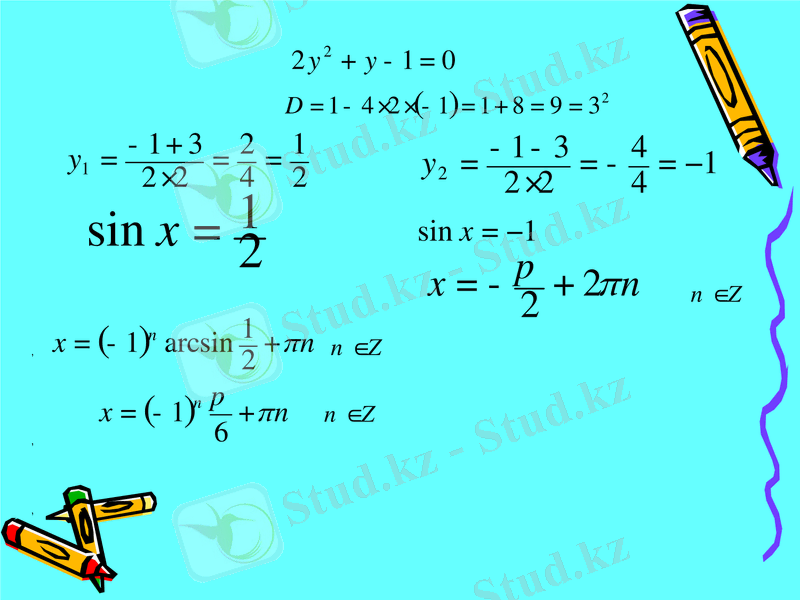







- Жаңа тақырып бойынша студенттердың білімін пысықтау (20-25 мин) -
№ 164. Теңдеулерді шешіңіздер:
а)
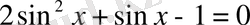
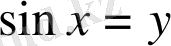 .
.
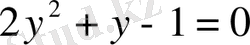
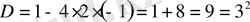
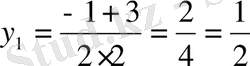
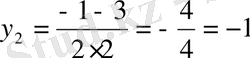
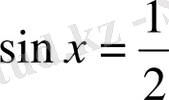
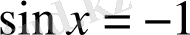
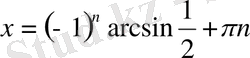 ,
,

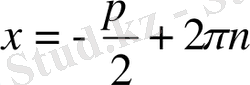 ,
,

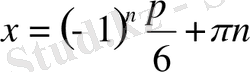 ,
,

б)
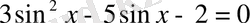
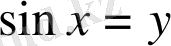
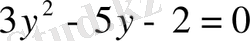
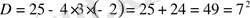
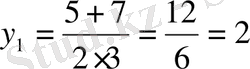
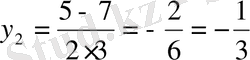
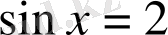
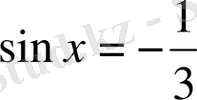
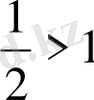 шешімі жоқ
шешімі жоқ
 ,
,

г)
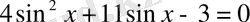
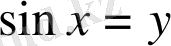
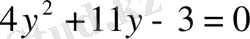
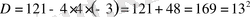
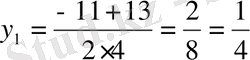
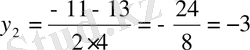
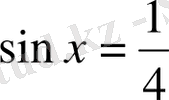
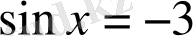
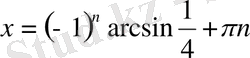 ,
,

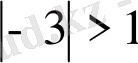 шешімі жоқ
шешімі жоқ
№ 165. Теңдеуді шешіңіздер:
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz