Постер қорғау арқылы теоремаларды дәлелдеу

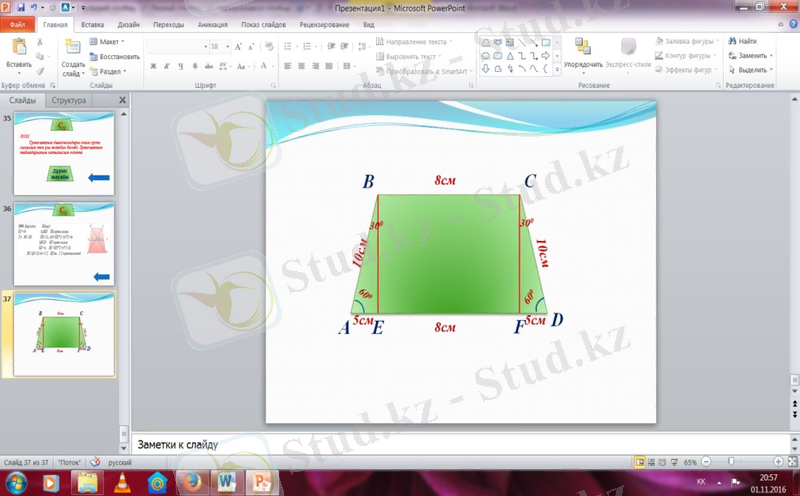
№70 Берілгені: Шешуі:

ABCD - тең бүйірлі AB=CD=10 см

Трапеция BC=EF=8 см

BC=8 см <B=30 ⁰ ;

AB=10 см AE=FD=AB/2=10 см/2=5 см

<A=60 ⁰ AD=AE+EF+FD=

Т/к P _ABCD =5 см+8 см+5 см=18 см

P _ABCD =AB+BC+CD+AD=

=10 см+8 см+10 см+18 см=46 см

Ж/бы: 46 см

№71 Берілгені: Шешуі:

ABCD - тең бүйірлі <A=<D=x

<A-<С=56 ⁰ <B+<С=y

Т/к <A, <B, <С, <D

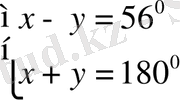
2x=236 x=118 ⁰

118 ⁰ +y=180 ⁰

y=62 ⁰

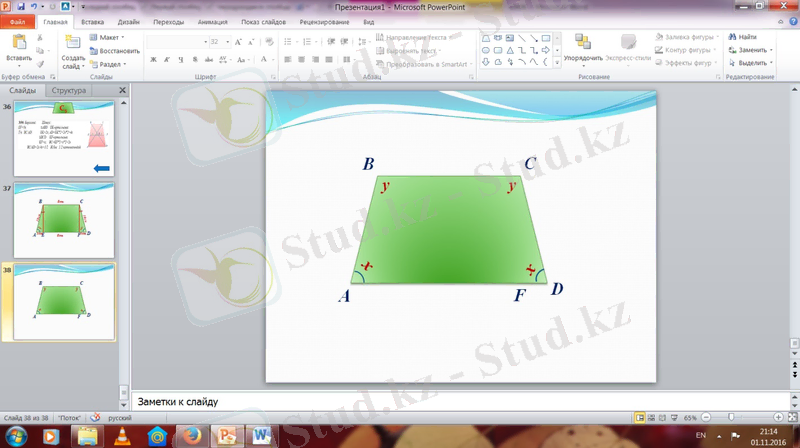Ж/бы: 118 ⁰ ; 62 ⁰ ; 118 ⁰ ; 62 ⁰ ;

What is a triangle?

One of the three points is not a straight line, and points to a figure called a triangle of strokes that.

Теорема 1. Үшбұрыштың екі қабырғасының ортасын қосатын орта сызық үшінші қабырғаға параллель және оның жартысына тең.

Дәлелдеу(1 бөлігі) АВС үшбұрыш берілсін. DЕорта сызығын жүргізіп, DЕ║АВ болатынын дәлелдейміз.

DЕ сәулесінің бойына Е нүктесінен әрі жалғастырып ЕF=DE кесіндісін өлшеп саламыз. Сонда ∆CED=∆BEF болады. Үшбұрыштар теңдігінің бірінші белгісі бойынша. Бұл жерде EF=DE, CE=BE және <1 = <2 вертикаль бұрыштар. Бұдан DC=BF (1) және <3 = <4 (2) . Сондықтан AD=DC=BF (3) Айқыш бұрыштардың теңдігінен, яғни (2) -ден DС║BF немесе AD║BF шығады. (4) Сонда (3) пен (4) - тен ABFD төртбұрышы параллелограмм болып тұр. Олай болса, DЕ║АВ

(2 бөлігі) DF=AB болғандықтан, Е нүктесі DF кесіндісінің қақ ортасын болғандықтан DE= 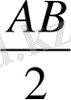болады. Теорема дәлелденді.

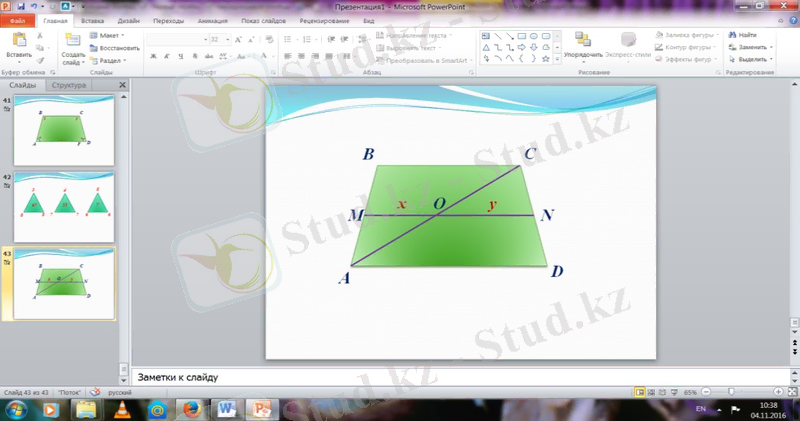
Теорема 2. Трапецияның орта сызығы табандарына параллель және табандарының қосындысының жартысына тең.

Дәлелдеу. (1 - бөлігі) ABCD трапециясы берілген болсын. EF орта сызығы болсын. ЕF║АВ, ЕF║DC болатынын дәлелдейміз.

AD бүйір қабырғасының ортасы Е нүктесі арқылы AB және DC табандарына параллель түзу жүргізсек, ол ВС бүйірін F нүктесінде қиып отеді. AE=ED болғандықтан, Фалес теоремасы бойынша BF=FC. Олай болса, EF - трапецияның орта сызығы. Өзіміздің сұрауымыз бойынша, ЕF║АВ, ЕF║DC. Демек, теореманың бірінші бөлігі дәлелденді.

F

E

D

A

B

C

Трапецияның BD диагоналін жүргізсек Фалес теоремасы бойынша О нүктесі BD кесіндісінің ортасы болады. Ендеше, FO және OF кесінділері сәйкесінде ABD, BCD үшбұрыштарының орта сызықтары: 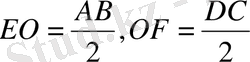оларды қоссақ, 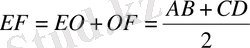аламыз. Теореманың 2 - бөлігі дәлелденді.

О

F

E

B

C

D

A

№77

C

1. Берілгені: Шешуі:

C

F

E

B

АВС - үшбұрыш

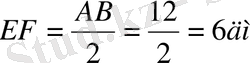
АВ=12дм

A

Т/к EF-? Ж/бы: 6 дм

№77

2. Берілгені: Шешуі:

F

E

B

АВС - үшбұрыш

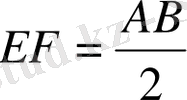
EF=4. 5 см AB=2EF=2*4. 5=9см

A

Т/к AB-? Ж/бы: 9см

№78 Берілгені: Шешуі:

C

АВ=6м

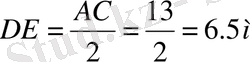
F

E

D

A

B

BC=9м

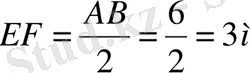
AC=13м

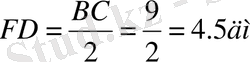
Т/к DE, EF, FD - ? Ж/бы: 6, 5м; 3м; 4, 5м;

№79 Берілгені: Шешуі:

C

DE=5дм AB=EF*2=7*2=14дм

F

E

D

A

EF=7дм BC=FD*2=10*2=20дм

FD=10дм AC=DE*2=5*2=10дм

Т/к AB, BC, AC - ? Ж/бы: 14дм; 20дм; 10дм;

B

№80 Берілгені Шешуі

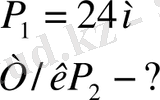
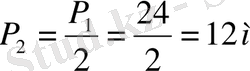Ж/бы: 12м

№81 Берілгені Шешуі

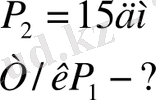P ₁ =2P ₂ =2*15дм=30дм Ж/бы: 30дм

№83 Берілгені Шешуі

C

AB=4x P _ABC = P _DEF *2=3. 6дм*2=7. 2дм

F

E

BC=3x 4x+3x+5x=7. 2

AC=5x 12x=7. 2 x=0. 6

P _DEF =3. 6 дм AB=4*0. 6=2. 4дм

Т/к x-? BC=3*0. 6=1. 8дм

D

A

B

AC=5*0. 6=3дм Ж/бы: 2, 4 дм; 1, 8 дм; 3 дм;

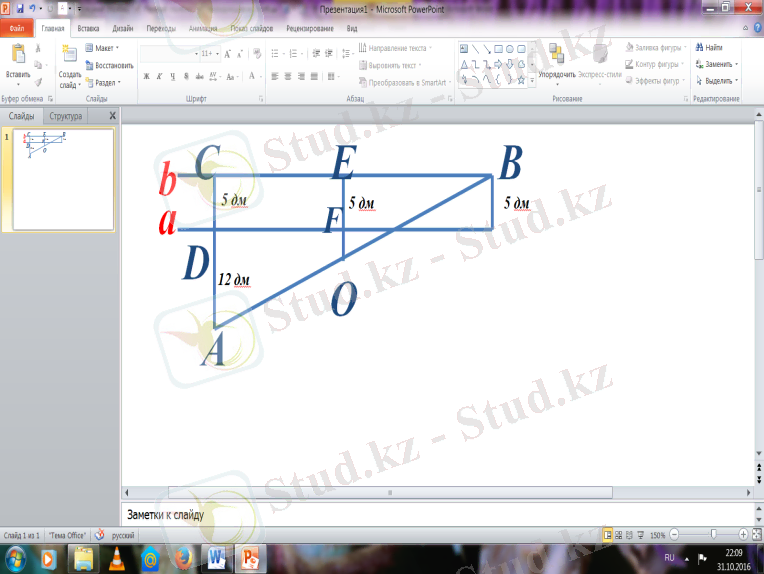№84 Берілгені Шешуі:

AD=12 дм BE=EF=CD=5дм

BE=5 дм AC=AD+DC=17 дм

Т/к OF - ? ∆ABC үшбұрыш

EO - орта сызық

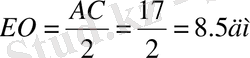
OF=8. 5-5=3. 5дм Ж/бы: 3, 5 дм

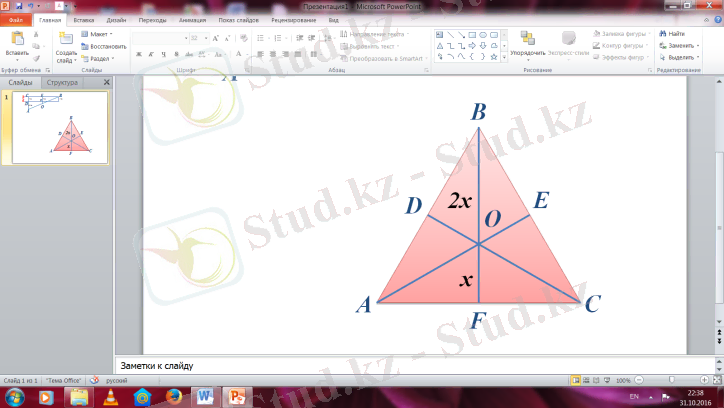№88 Берілгені Шешуі:

∆ABC үшбұрыш BO=2x

BF=6 м OF=x

т/к BO, OF-? 2x+x=6

3x=6 x=2

OF=2м, BO=2*2м=4м Ж/бы: 2м; 4м;

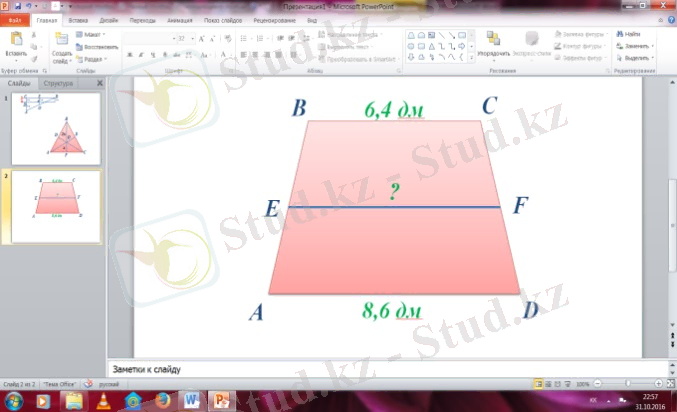№91 Берілгені : Шешуі:

ABCD - трапеция

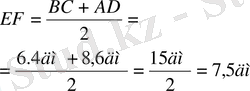
BC=6. 4дм

AD=8. 6 дм Ж/бы: 7, 5 дм

Т/к EF - ?

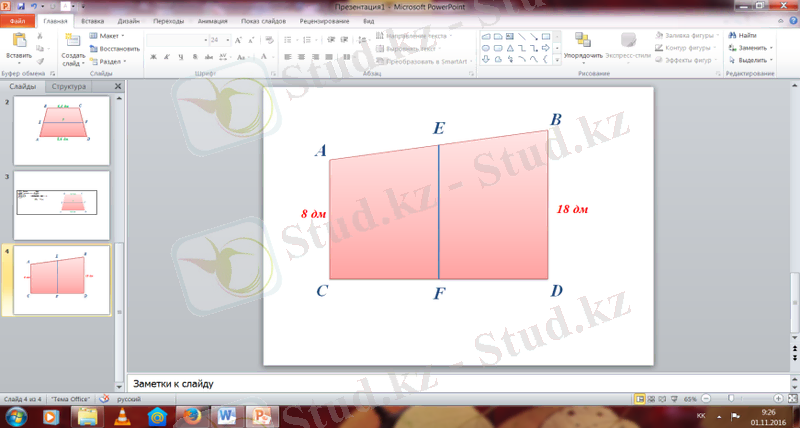№92 Берілгені: Шешуі:

1. Жағдай

AC=8 дм

BD=18 дм Ж/бы: 13 дм

Т/к EF - ?

2. Жағдай Шешуі:

Берілгені AF=KB=8 дм

AE=18 дм EF=AE+AF=18 дм+8 дм=26 дм

KB=8 дм OL=EF/2=26/2=13 дм

Т/к OD - ? OD=OL-DL=13 дм-8 дм=5 дм Ж/бы: 5 дм

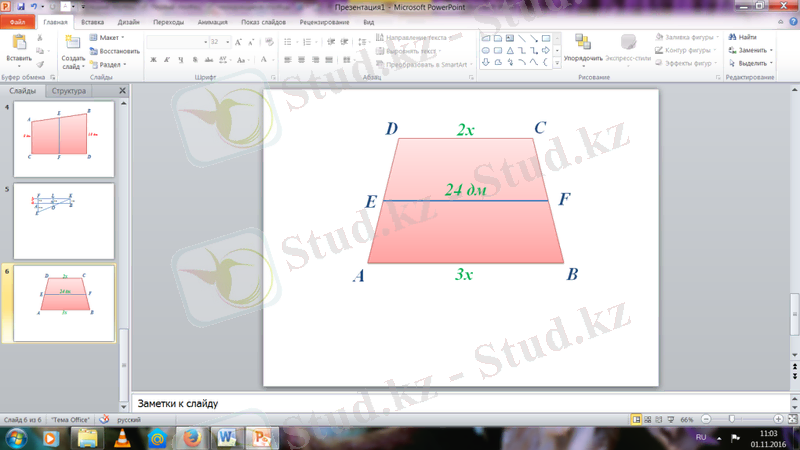№93 Берілгені: Шешуі:

DC=2x EF=(DC+AB) /2

AB=3x (2x+3x) /2=24 дм

EF=24 дм 5x/2=24

Т/к DC, AB - ? 5x=48 x=9. 6

DC=2*9. 6=19. 2 дм

AB=3*9. 6=28. 8 дм

Ж/бы: 19, 2 дм; 28, 8 дм

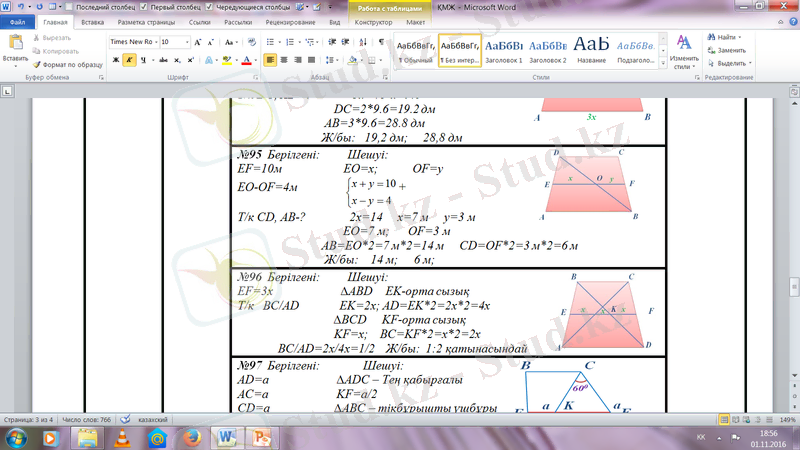№95 Берілгені: Шешуі:

EF=10м EO=x; OF=y

EO-OF=4м +

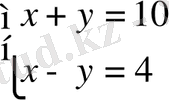Т/к CD, AB-? 2x=14 x=7 м y=3 м

EO=7 м; OF=3 м

AB=EO*2=7 м*2=14 м CD=OF*2=3 м*2=6 м

Ж/бы: 14 м; 6 м;

№96 Берілгені: Шешуі:

EF=3x ∆ABD EK-орта сызық

Т/к BC/AD EK=2x; AD=EK*2=2x*2=4x

∆BCD KF-орта сызық

KF=x; BC=KF*2=x*2=2x

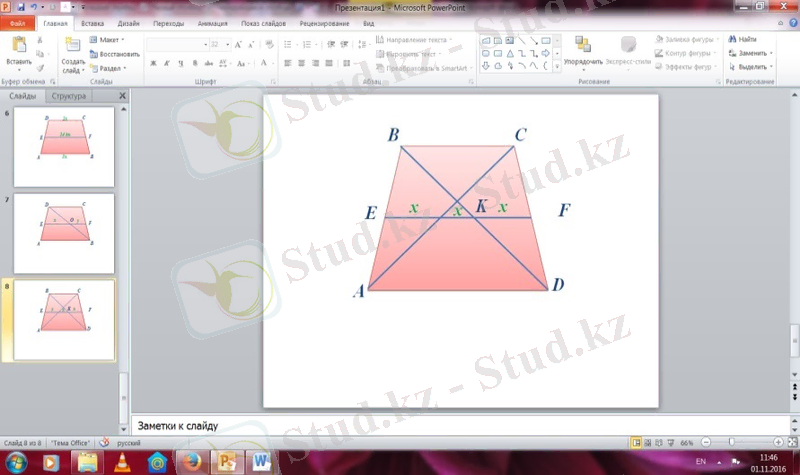BC/AD=2x/4x=1/2 Ж/бы: 1:2 қатынасындай

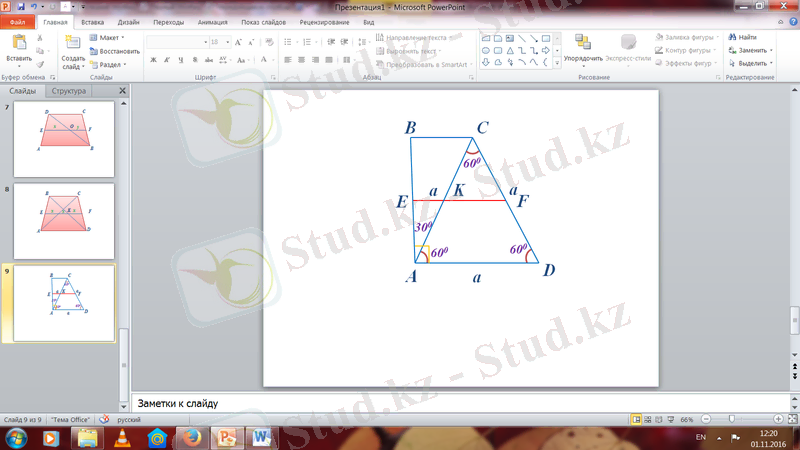№97 Берілгені: Шешуі:

AD=a ∆ADC - Тең қабырғалы

AC=a KF=a/2

CD=a ∆ABC - тікбұрышты үшбұрыш

Т/к EF-? BC=AC/2=a/2

EK=a/2:2=a/4

EF=EK+KF=a/2+a/4=3a/4

Ж/бы: 3а/4

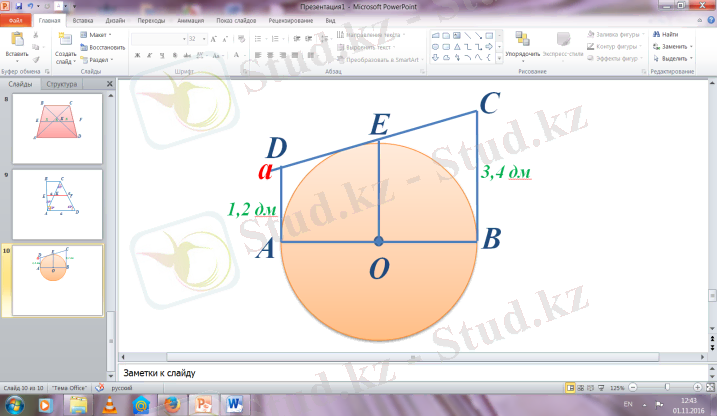№101 Берілгені: Шешуі:

AD=1. 2 дм ABCD - трапеция

BC=3. 4 дм EO - орта сызық,

Т/к AB-? шеңбердің радиусы

EO=(AD+BC) /2=(1. 2 дм +3. 4 дм) /2=

=4. 6 дм /2=2. 3 дм

AB=EO*2=2. 3 дм*2=4. 6 дм

Ж/бы: 4, 6 дм

№6 Берілгені: Шешуі:

ABCD трапеция, BC║AD ∆ABC - нан:

BC=4cм, AD=10 cм x=BC/2=4/2=2 cм

Т/к: x-? y-? ∆ACD - нан:

y=AD/2=10/2=5 cм

Ж/бы: 2 cм